Условия, при которых матрица подобна диагональной матрице

Пусть A – квадратная матрица. Можно считать, что это матрица некоторого линейного оператора, заданного в каком-то базисе. Известно, что в другом базисематрица линейного оператора примет другой вид, в частности, как в одном из предыдущих примеров 9.3, диагональный. Это значит, что исходная матрица подобна диагональной матрице. Возникает вопрос: всегда ли данная матрица подобнадиагональной? Как это установить? Как найти соответствующий базис?

Теорема 9.14. Матрица A подобна диагональной матрицетогда и только тогда, когда линейный операторj, заданныйэтой матрицей, имеет n линейно независимых собственных векторов.

Доказательство. Пусть матрица A подобна диагональной матрице, то естьулинейного оператораj сматрицей A = M(j) внекоторомбазисе с₁, с₂, …, с_n матрица примет следующий вид M '(j) = 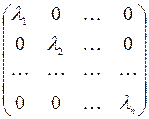.Используяматрицу, найдемобразы базисных векторов: j(с₁) = l₁с₁, j(с₂) = l₂с₂, …, j(с_n) = l_nс_n. Получены n линейно независимых собственных векторов.

У линейного оператораj есть n линейно независимых собственных векторов с₁, с₂, …, с_n ссобственнымизначениями l₁, l₂, …, l_n. Выберем векторы с₁, с₂, …, с_n в качестве базисных векторов и найдем матрицу оператораj в этом базисе. Используя равенства j(с₁) = l₁с₁, j(с₂) = l₂с₂, …, j(с_n) = l_nс_n составим матрицу M '(j): M '(j) = .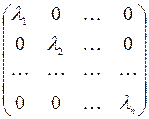

Теорема 9.15. Если матрица A имеет n попарно различных собственных значений, то она подобна диагональной матрице.

Это утверждение основано на свойстве собственных векторов: попарно различным собственнымзначениям соответствуютлинейно независимыесобственныевекторы.

Пример 9.8. Привести матрицу A к диагональномувиду, если это возможно, указать базис и матрицу перехода.

1)A = 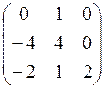.Для этого случая собственные векторы уже найдены (пример 9.7), линейно независимых векторовоказалось только 2, а в базисе должно быть 3. Вывод: матрица A к диагональномувиду не приводится.Другими словами: матрица A не подобна диагональной.

2)A = .Находим собственные значения матрицы A. Вычислим определитель

|A – lE| = = =

=(1 – l) = (1 – l) =

= (1 – l)×1×(–1)^{2 + 2}× = (1 – l)((7 – l)(–7 – l) – 6(–8)) =

= (1 – l)(l² – 1) = –(l + 1)(l – 1)² = 0. Тогда l₁ = l₂ = 1, l₃ = –1 – собственные значения матрицы A.

Находим собственные векторы, соответствующие этим собственнымзначениям. Рассмотрим случай l₁ = l₂ = 1. Решаем однороднуюсистему линейныхуравнений ~ (1 –2 1), тогда х₁ = 2х₂ – х₃ –общее решение системы, векторы с₁ = (2, 1, 0) с₂ = (1, 0, –1) линейно независимые собственные векторы с собственнымзначением l₁ = l₂ = 1.

Рассмотрим случай l₃ = –1. Получаем систему . Решая ее, получим только один линейно независимыйсобственныйвектор с₃ = (3, 5, 6).

Найдены три линейно независимыхсобственныхвектора с₁, с₂, с₃. Выберем их в качестве нового базиса и найдем матрицу линейного оператора в этом базисе.

Поскольку j(с₁) = 1с₁, j(с₂) = 1с₂, j(с₃) = (–1)с₃, то матрица линейного оператора M '(j) = и T = –матрица перехода от старого базиса к новому.