Численное дифференцирование.
При решении многих практических задач возникает необходимость получить значения производных различных порядков функции 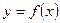 , заданной в виде таблицы или сложного аналитического выражения. В этих случаях применить непосредственно методы дифференциального исчисления либо невозможно, либо затруднительно. Простейшие выражения для производных получаются в результате дифференцирования интерполяционных формул.
, заданной в виде таблицы или сложного аналитического выражения. В этих случаях применить непосредственно методы дифференциального исчисления либо невозможно, либо затруднительно. Простейшие выражения для производных получаются в результате дифференцирования интерполяционных формул.
Пусть на сетке 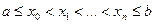 для непрерывно дифференцируемой n+1+m раз функции
для непрерывно дифференцируемой n+1+m раз функции 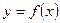 заданы значения
заданы значения 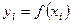 для равноотстоящих значений независимой переменной:
для равноотстоящих значений независимой переменной: 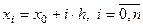 , где h − шаг интерполяции,
, где h − шаг интерполяции, 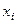 - узлы интерполяции. Требуется вычислить производную
- узлы интерполяции. Требуется вычислить производную 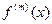 ,
, 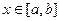 .
.
В основе численного дифференцирования лежит аппроксимация функции, от которой берется производная, интерполяционным многочленом. В качестве интерполяционных многочленов берут многочлены Стирлинга, Бесселя, Ньютона.
Построим для функции f по узлам 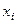 интерполяционный многочлен с остаточным членом Rn:
интерполяционный многочлен с остаточным членом Rn: 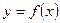 = Pn(x) +Rn(x) и продифференцируем левую и правую части по х m раз, положив х = х*. Для достаточно гладких функций, достаточного количества узлов и достаточной точности вычислений величина
= Pn(x) +Rn(x) и продифференцируем левую и правую части по х m раз, положив х = х*. Для достаточно гладких функций, достаточного количества узлов и достаточной точности вычислений величина 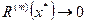 , тогда получим, что
, тогда получим, что
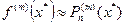 .
.
Получим формулы для нахождения производных плюс-минус погрешность.
Дифференцируя интерполяционный многочлен Стирлинга два раза, выразив входящие в него конечные разности непосредственно через значения функций, получим формулы для первой и второй производной в точке х0:
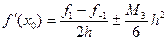 , (1)
, (1)
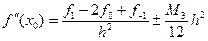 . (2)
. (2)
Дифференцируя интерполяционный многочлен Бесселя, получим формулу для первой производной в точке 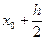 - в середине между узлами:
- в середине между узлами:
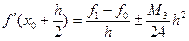 . (3)
. (3)
Дифференцируя первый и второй интерполяционный многочлен Ньютона, получим формулы для первой производной в точке 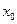 :
:
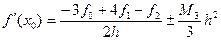 , (4)
, (4)
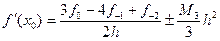 . (5)
. (5)
Суммарная погрешность составляет 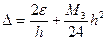 .
.
Из приведенных выше формул видно, что с уменьшением шага сетки (в определенных пределах) уменьшается и погрешность метода. При вычислении производных следует определить оптимальный шаг исходной таблицы значений.
Для оптимального шага из формулы (2) получаем выражение 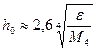 , из формулы (3) – выражение
, из формулы (3) – выражение 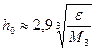 , из формул (4) и (5) – выражение
, из формул (4) и (5) – выражение 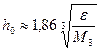 . Где
. Где 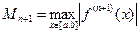 .
.
Одним из универсальных способов построения формул численного дифференцирования состоит в том, что по значениям функции в некоторых узлах строят интерполяционный многочлен в форме Лагранжа или в форме Ньютона и полагают, что 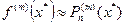 . В ряде случае наряду с приближенным равенством удается получить точное равенство, содержащее остаточный член (погрешность дифференцирования).
. В ряде случае наряду с приближенным равенством удается получить точное равенство, содержащее остаточный член (погрешность дифференцирования). 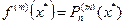 +R. Такие формулы называются формулами численного дифференцирования с остаточными членами.
+R. Такие формулы называются формулами численного дифференцирования с остаточными членами.
Приведем несколько распространенных формул численного дифференцирования с остаточными членами для первой и второй производных в узлах с постоянным шагом h. 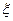 - некоторая промежуточная точка.
- некоторая промежуточная точка.
1) Первая производная, два узла.
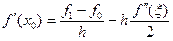 ,
, 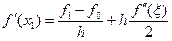
2) Первая производная, три узла.
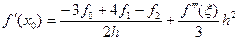
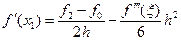 (6)
(6)
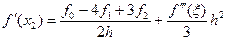
3) Вторая производная и три узла.
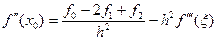
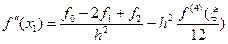
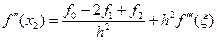
4) Вторая производная и четыре узла.
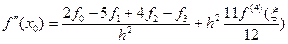
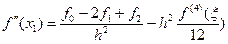 (7)
(7)
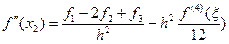
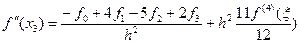
Формулы с отброшенными остаточными членами называются просто формулами численного дифференцирования.
В некоторых случаях для определения производных задается только таблица значений функции. Тогда оценить погрешность, очевидно, невозможно, как и подобрать оптимальный шаг. Приближенные значения производных вычисляются непосредственно по одной из формул без учета погрешности.
Пример 1.
Вычислить 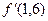 и
и 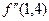 для функции
для функции 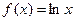 , заданной в виде следующей таблицы:
, заданной в виде следующей таблицы:
| x | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 |
| f(x) | 0,1823 | 0,2626 | 0,3364 | 0,4054 | 0,47 |
Оценить погрешность результата. ε = 2∙10-4.
Решение.
Для нахождения оптимального шага, вычислим значения М3 и М4. Сначала найдем производные: 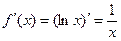 ,
, 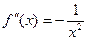 ,
, 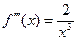 ,
, 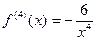 .
.
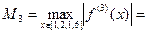 330,1186
330,1186 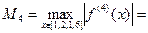 5432,5584
5432,5584
Найдем оптимальный шаг для первой производной 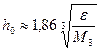 = 0,1.
= 0,1.
Найдем оптимальный шаг для второй производной 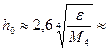 0,2.
0,2.
Для нахождения производных применим формулы (2) и (5).
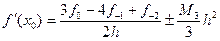 , тогда
, тогда 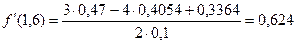 .
.
Суммарная погрешность не превышает 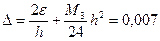 .
.
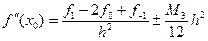 , тогда
, тогда 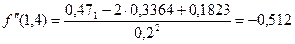
Суммарная погрешность 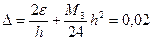 .
.
Пример 2.
Вычислить 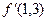 и
и 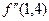 для функции
для функции 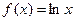 , заданной в виде следующей таблицы:
, заданной в виде следующей таблицы:
| x | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 |
| f(x) | 0,18 | 0,26 | 0,34 | 0,41 | 0,47 |
Решение.
Применим формулу (4). Шаг h = 0,1.
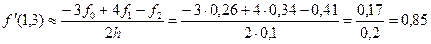 .
.
Применим формулу (6) без погрешности:
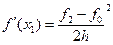 , тогда
, тогда 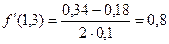
Применим формулу (2).
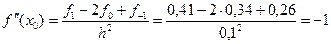 .
.
Применим формулу (7) без погрешности:
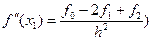 , тогда
, тогда 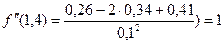 .
.
Дата добавления: 2016-06-15; просмотров: 9861;










