Линеаризация уравнений

В теории управления лучше всего разработаны методы исследования линейных систем. Однако строго линейных систем в окружающем нас мире не существует. Поэтому для того, чтобы эти методы можно было применить на практике, нужно выполнить линеаризацию – построить приближенную линейную модель на основе более реалистичной нелинейной модели объекта.

Алгебраические уравнения

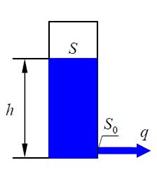Представим себе бак с водой. В нижней части бака просверлено отверстие, через которое вытекает вода. Площадь сечения бака обозначим через S, а площадь сечения отверстия – через S₀. Построим модель, которая связывает уровень воды в баке h (в метрах) и расход вытекающей воды q (в м³/с). Эту связь можно найти с помощью закона Бернулли, который в данном случае принимает вид:

.

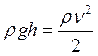Здесь ρ – плотность жидкости (в кг/м³), g ≈ 9,81м/с² – ускорение свободного падения, v – скорость вытекания жидкости (в м/с). Отсюда получаем v = 2gh. Учитывая, что расход воды вычисляется как q=S₀⋅v, находим

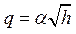, (2)

где 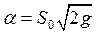– постоянная величина. Это статическая модель, потому что она не содержит производных, характеризующих изменение сигналов во времени. Статическая модель описывает установившееся состояние (статический режим), когда в баке поддерживается постоянный уровень воды и поток вытекающей воды тоже постоянный.

Очевидно, что модель (2) – нелинейная, поскольку содержит 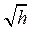. Линеаризовать ее – значит приближенно заменить уравнение (2) линейным уравнением q = k⋅h , где k – некоторый коэффициент. Как его выбрать? На этот вопрос нет однозначного ответа.

Предположим, что уровень воды изменяется в интервале от 0 до 1 м. Тогда один из вариантов – вычислить коэффициент как угол наклона отрезка, соединяющего точки кривой 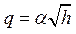на концах этого интервала. Для определенности далее везде принимаем α = 1, тогда получаем k =1.

Конечно, эта модель очень грубая и дает большую ошибку, особенно для уровней в диапазоне от 0,1 до 0,6. Чтобы уменьшить ошибку, можно попробовать несколько изменить k (например, увеличив его до 1,2), однако точность приближения по-прежнему будет невысока, хотя и чуть-чуть лучше, чем в первом случае.

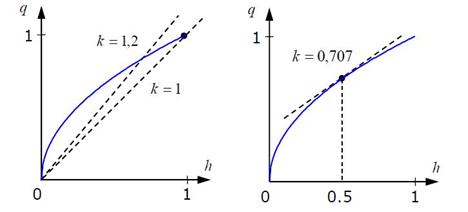
Рисунок 2.2 – Зависимость q от h

Теперь предположим, что обычно уровень мало изменяется вблизи среднего значения h = 0,5м. В этом случае можно применить другой подход. Заметим, что в этой области кривая 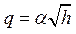почти совпадает с касательной в точке (0,5; 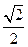), угол наклона которой равен производной

.

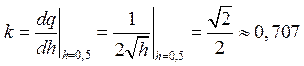Касательная – это прямая с наклоном k, проходящая через точку (0,5; 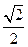), ее уравнение имеет вид q = kh + b. Свободный член b определим из равенства

,

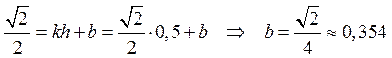так что получаем модель

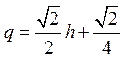. (3)

Это линейное уравнение, однако модель (3) – нелинейная, поскольку для нее не выполняется свойство умножения на константу и принцип суперпозиции.

Для того чтобы получить из (3) линейную модель, нужно записать уравнения в отклоненияхот рабочей точки (h₀; q₀), в которой мы определяли наклон касательной. Из (3) следует, что

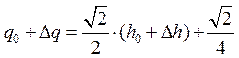. (4)

Поскольку график зависимости (3) проходит через точку (h₀; q₀), можно применить равенство 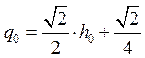. Тогда из (4) получим

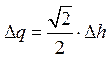. (5)

Полученное таким образом уравнение – это линейная модель объекта, записанная в отклонениях входа и выхода от номинальной (рабочей) точки (h₀; q₀). Приближенная модель (5) точнее всего соответствует объекту вблизи этой точки, а при больших отклонениях от нее ошибка может значительно возрастать.

Управление

Посмотрим на примере, как можно управлять объектом и что из этого получается. Немного изменим предыдущую задачу, разрешив потоку вытекающей жидкости q изменяться независимо (в теории управления это называется нагрузкой на объект).

Для того, чтобы обеспечить водой всех жителей деревни, построили водонапорную башню, в которую насосом закачивается вода из реки. Каждый житель может в любой момент включить воду на своем участке, например, для полива. Нужно построить систему, которая автоматически поддерживает заданный уровень h₀ воды в цистерне (в метрах).

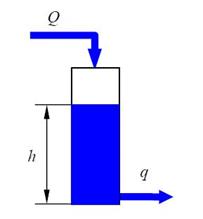Будем считать, что жителей довольно много, поэтому у кого-то всегда включена вода и насос постоянно работает на закачку воды в цистерну. Для управления уровнем воды h мы можем изменять его поток Q (в м³/с). Таким образом, уровень h – это регулируемая величина, а поток Q – сигнал управления. Для обратной связи используем датчик, измеряющий уровень воды h в цистерне.

Построим математическую модель объекта, то есть цистерны. Поток на выходе q (в м³/с) показывает, сколько воды вытекает из цистерны за 1 с – это нагрузка.

Изменение уровня Δh зависит от разности потоков Q−q и площади сечения цистерны S. Если разность потоков постоянна в течение интервала времени Δt, то 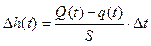. В общем случае нужно использовать интеграл

.

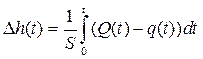Пусть в момент времени t = 0 уровень воды равен заданному значению, а входной и выходной потоки равны (Q(0)=q(0)=q₀), так что уровень не меняется. Этот режим мы примем за номинальный (рабочую точку). Для того, чтобы получить уравнение в отклонениях, представим потоки в виде

,

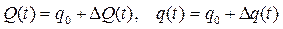где ΔQ(t) и Δq(t) – малые отклонения потоков от номинального режима. Тогда, опуская знак приращения Δ, можно записать модель объекта управления в форме

.

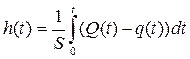Здесь h(t), Q(t) и q(t) обозначают отклонения этих величин от номинальных значений. Заметим, что эта модель может быть записана как дифференциальное уравнение (если найти производные обеих частей равенства):

.

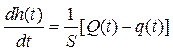Для упрощения далее примем S = 1м².

В качестве обратной связи мы будем использовать сигнал с датчика уровня. Ошибка управления вычисляется как разница между заданным и измеренным уровнями воды:

.

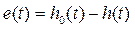Применим самый простой регулятор – усилитель с коэффициентом K (или пропорциональный регулятор, П-регулятор), который управляет потоком по закону

.

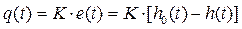Структурная схема системы управления показана на рисунке ниже. Знак интеграла обозначает звено, модель которого – оператор интегрирования. С помощью кружка с секторами обозначается сложение сигналов. Если какой-то сектор закрашен черным цветом, входящий в него сигнал вычитается (учитывается в сумме со знаком «минус»). Кроме сигналов, о которых уже шла речь, на рисунке показан также шум измерения m(t) , искажающий показания датчика.

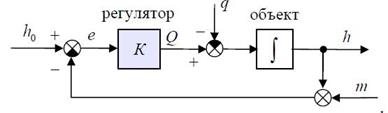
Рисунок 2.3 – Структурная схема СУ

Проверим работу этого регулятора при различных значениях коэффициента K. Сначала будем считать, что шума измерений нет, то есть уровень измеряется точно. Предположим, что расход воды на выходе q увеличивается скачком. Синяя линия на рисунке (см. ниже) показывает изменение уровня при K = 1, а зеленая – при K = 5 .

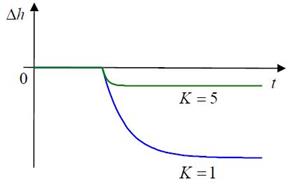
Рисунок 2.4 – График переходной функции

По этим данным можно сделать некоторые выводы:

• при изменении нагрузки (потребления воды, потока q) регулятор-усилитель не может поддерживать заданный уровень (графики не приходят к значению Δh = 0);

• чем больше К, тем меньше ошибка регулирования Δh в установившемся режиме; можно ожидать, что при K →∞ ошибка должна уменьшиться до нуля;

• чем больше К, тем быстрее заканчивается переход на новый режим.

Кажется, что для улучшения управления нужно увеличивать K, однако это только первое впечатление.

Теперь посмотрим, что будет, если есть шум измерений (случайная ошибка датчика).

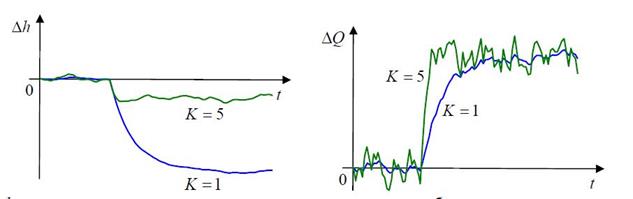
а) б)

Рисунок 2.5 – График: а) переходной функции, б) изменения расхода

По графикам видно, что при неточных измерениях уровень колеблется около некоторого среднего значения (того, что было получено без шума), причем при большем K колебания увеличиваются. Этот эффект особенно хорошо виден на графике изменения расхода насоса Δq (рисунок справа).

При увеличении K повышение точности (уменьшение установившейся ошибки) достигается за счет повышенной активности насоса, который все время «дергается». При этом механические части изнашиваются, и существенно уменьшается его срок службы. Поэтому коэффициент K нельзя сильно увеличивать.

Один из главных выводов этого примера: управление чаще всего связано с компромиссом. Здесь, с одной стороны, нужно увеличивать K, чтобы повысить точность, а с другой – нужно уменьшать K, чтобы уменьшить влияние шума измерения.