Второе начало термодинамики

Первое начало термодинамики представляет собой математическое выражение закона сохранения и превращения энергии, но не определяет условий возможности таких преобразований. Согласно этому закону возможен переход теплоты от более горячего тела к более холодному и наоборот, от холодного к горячему. Между тем реальные процессы, происходящие вокруг нас, как правило, необратимы, то есть они самопроизвольно идут только в одном направлении – в направлении установления термодинамического равновесия в системе.

Для производства работы путем использования теплоты в тепловом двигателе рабочее тело должно расширяться. Если мы хотим выполнять работу безостановочно продолжительное время, то это требует непрерывного повторения рабочим телом процесса расширения. Такой процесс реально можно осуществить двумя путями. Первый путь – рабочее тело расширяется и удаляется из двигателя, а на его место поступает новая порция рабочего тела, которая вновь расширяется. В этом случае необходимо постоянно добавлять все новые порции рабочего вещества. Второй путь – рабочее тело расширяется, а затем путем сжатия возвращается в исходное состояние и цикл повторяется. В этом случае возможно обходиться одним и тем же объемом рабочего вещества, но на его сжатие придется затрачивать работу внешних сил. При этом очевидно, что для того чтобы получить от теплового двигателя полезную работу, работа по сжатию должна быть меньше работы, которую совершает рабочее тело при расширении.

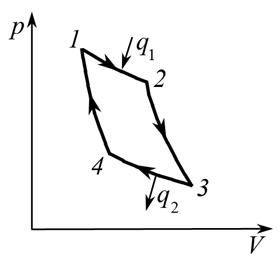
Будем рассматривать возможности второго пути получения работы. Схематично графически изменение состояния рабочего тела в координатах p – V представлено на рис. 9. В начальный момент цикла рабочее тело находится в состоянии A. Расширяясь, оно по кривой ACB переходит в состояние B. Затем сжимаясь, по кривой BDA возвращается в состояние A. Таким образом, рабочее тело попеременно расширяется и сжимается, возвращаясь каждый раз в исходное состояние. Такой замкнутый процесс называется круговым процессом или циклом.

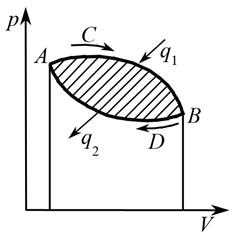
Рис. 9

Пусть на участке ACB к 1 кг рабочего тела подводится количество теплоты 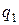, при этом его внутренняя энергия изменяется на величину 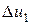и совершается работа 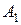. На участке BDA от рабочего тела отводится количество теплоты 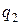, внутренняя энергия изменяется на 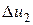и для сжатия газа внешними силами совершается работа 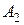. Согласно первому закону термодинамики для процесса расширения можно записать

.

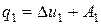Для участка сжатия

.

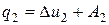Разность количества подведенной и отведенной теплоты запишется как

.

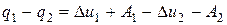Поскольку рабочее тело вернулось в исходное состояние его внутренняя энергия (зависящая только от параметров состояния) стала первоначальной поэтому 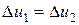. Разность 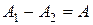представляет собой разность работы, совершенной рабочим телом при расширении и работы внешних сил по сжатию рабочего тела, то есть полезную работу, совершенную тепловым двигателем. Тогда получаем

,

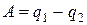то есть, полезная работа теплового двигателя определяется разностью подведенного и отведенного количества теплоты.

Степень использования теплоты в цикле характеризуется термическим коэффициентом полезного действия, равным отношению количества теплоты, превращенной в работу, к количеству затраченной теплоты

.

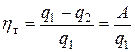Цикл Карно

Из всех возможных рабочих циклов, встречающихся в термодинамике, особое значение имеет так называемый цикл Карно. Французский инженер С. Карно предложил модель идеального цикла теплового двигателя, дающую максимальное значение термического коэффициента полезного действия.

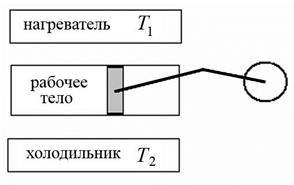
Физическая картина явлений, происходящих в цикле Карно, может быть представлена следующим образом (рис. 10). Двигатель для цикла Карно представляет собой теплоизолированный цилиндр с подвижным поршнем, в котором находится рабочее тело – идеальный газ. При этом рабочее тело может периодически сообщаться (соприкасаться) то с горячим источником теплоты (нагревателем) с температурой T₁, то с холодным телом (холодильником) с температурой T₂.

Рис. 10

Начало цикла в точке 1, где рабочее тело двигателя имеет параметры p₁, 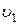, T₁ (рис. 10). С рабочим телом в соприкосновение приводится нагреватель, температура которого также равна T₁. Получая от нагревателя некоторое количество тепла q₁, газ начинает расширяться. При этом его температура остается постоянной и равной температуре нагревателя, то есть процесс происходит изотермически. Под влиянием повышающегося давления поршень двигателя начинает перемещаться вправо. Процесс продолжается до точки 2, в которой рабочее тело имеет параметры p₂, 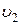, T₁. Здесь нагреватель отсоединяется от теплового двигателя, то есть, рабочее тело изолируется от нагревателя, и не получая теплоты, продолжает расширяться адиабатно, двигая поршень вправо. Адиабатный процесс расширения продолжается до точки 3, при этом температура рабочего тела понижается до величины T₂ < T₁. В этот момент поршень достигает своего крайне правого положения. Параметры рабочего тела в точке 3 равны p₃, 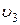, T₂. Обратное движение поршня происходит под действием энергии, накопленной в маховике и передаваемой посредством кривошипно-ползункового механизма. В точке 3 к двигателю присоединяется холодильник с температурой T₂. Рабочее тело начинает сжиматься, сжатие происходит также изотермически при постоянной температуре T₂, обеспечиваемой холодильником. Для того чтобы обеспечить процесс сжатия, необходимо от рабочего тела отвести количество тепла, q₂ < q₁, эквивалентное работе, затраченной на изотермическое сжатие. Процесс продолжается до состояния 4, в котором рабочее тело принимает параметры p₄, 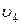, T_2. В точке 4 рабочее тело отсоединяется от охладителя и продолжает сжиматься адиабатно, при этом температура рабочего тела возрастает до T₁ и параметры рабочего тела вновь соответствуют параметрам в точке 1: давление и температура возрастают до значений p₁ и T₁, удельный объем уменьшается до первоначального значения .

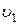Таким образом, получился цикл, состоящий из двух изотерм и двух адиабат. Термический КПД цикла Карно определяется по формуле

.

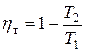(19)

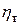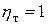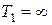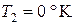Из выражения (19) видно, что термический КПД зависит только от температур T₁ и T₂, причем значение тем больше, чем больше температура нагревателя T₁ и меньше температура холодильника T₂. Получить значение можно лишь для значений или , однако понятно, что ни то, ни другое невозможно.

Карно теоретически доказал теорему о том, что невозможно построить периодически действующий тепловой двигатель с циклом, имеющим более высокий термический коэффициент полезного действия, чем КПД цикла Карно при одинаковых начальных и конечных температурах. В этом смысле КПД цикла Карно есть тот предел, к которому стремится КПД любого теплового двигателя. Поэтому в реальных тепловых двигателях для приближения их к циклу Карно и увеличения КПД стремятся увеличить температуру нагревателя и снизить температуру холодильника.

Кроме того, Карно также доказал следующую теорему: термический КПД цикла с двумя источниками теплоты (нагревателем и охладителем) не зависит от свойств рабочего тела цикла.

Цикл Карно является обратимым и его можно провести в направлении, противоположном уже рассмотренному. В этом случае от холодильника, имеющего температуру T₂, отводится количество теплоты q₂ и передается нагревателю, имеющему температуру T₁ > T₂. Так как теплота от менее нагретого тела самопроизвольно не передается более нагретому телу, для реализации этого процесса необходимо затратить определенную работу. При этом если от холодильника отводится количество теплоты q₂, то нагревателю передается количество теплоты 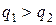и

.

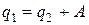Обратный цикл Карно является идеальным циклом холодильной машины. Для оценки эффективности холодильной машины вводится холодильный коэффициент

ϰ = .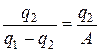

Холодильный коэффициент цикла Карно равен

ϰ = ,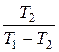

то есть зависит только от температур холодильника и нагревателя, и в отличие от КПД, всегда больше единицы.