Первый закон термодинамики

Как уже определялось выше, состояние термодинамической системы газа может быть равновесным и неравновесным. Равновесным называется такое состояние газа, при котором его параметры (p, T, 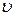) остаются неизменными сколь угодно долго, пока какие-то внешние воздействия не выведут систему из равновесия.

Если термодинамический процесс совершается настолько медленно, что, изменяясь, параметры успевают выравниваться по всей системе и разностью параметров в различных частях системы можно пренебречь на всем протяжении перехода из одного состояния в другое, такой переход можно считать равновесным переходом (состоящим из непрерывного числа равновесных состояний). Очевидно, что при быстром переходе из одного состояния системы в другое равенство параметров газа в разных частях системы не будет соблюдаться и процесс будет неравновесным. Все реальные процессы неравновесны.

Равновесный процесс можно представить графически (рис. 1) в прямоугольной системе координат, откладывая на горизонтальной оси значения объема V газа, а на вертикальной оси – значения давления p. Тогда процесс будет иметь вид линии, то есть, совокупности точек, соответствующих определенным временным равновесным состояниям.

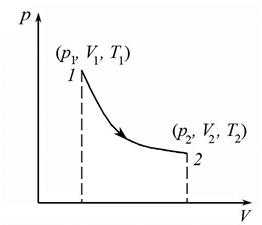
Рис. 1

Пусть в результате термодинамического процесса система из состояния 1 с параметрами p₁, T₁, 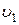перешла в состояние 2 с параметрами p₂, T₂, 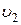– назовем этот процесс прямым. Тогда любой процесс, приводящий систему из состояния 2 в состояние 1, называется обратным (например, если расширение газа считать прямым процессом, то сжатие – процесс обратный).

Термодинамические процессы могут быть обратимыми и необратимыми.

Обратимым называется равновесный процесс, который в прямом и в обратном направлениях протекает через один и тот же ряд равновесных состояний, не вызывая в итоге изменений в самом газе и в телах, окружающих систему. Неравновесные процессы необратимы.

Газ, находящийся в сосуде при давлении больше атмосферного, стремиться расшириться, то есть увеличить занимаемый им объем. При этом ему приходится преодолевать сопротивление внешних сил, совершая работу по их преодолению. Попробуем оценить эту работу.

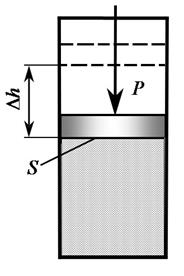
Пусть некоторый объем газа с параметрами p, T, V находится в цилиндре под поршнем, который может скользить без трения (рис. 2).

Рис. 2	Рис. 3

К поршню приложена внешняя сила P. Пусть в результате подвода теплоты газ расширился так, что его давление осталось неизменным, а объем увеличился, при этом поршень переместился на расстояние 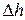. На преодоление внешней силы газ затратил работу, равную произведению силы на пройденный путь. Если площадь поперечного сечения поршня S, то сила давления равна 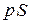, а совершенная работа 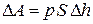. Произведение площади сечения поршня на перемещение – это изменение объема газа 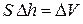. Тогда

.

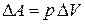(7)

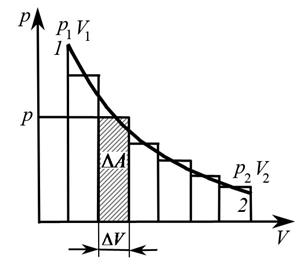
В общем случае для определения работы газа, который в результате термодинамического процесса перешел из состояния 1 в состояние 2 (рис. 3), необходимо разбить кривую переходного процесса на большое количество элементарных участков, на каждом из которых давление можно считать постоянным. И на каждом элементарном участке будет справедлива зависимость (7). При дальнейшем уменьшении размеров участков перейдем к дифференциалам:

.

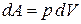(8)

Из формулы (8) видно, что если газ расширяется ( 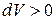), то он совершает положительную работу по преодолению внешних сил ( 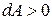). Если газ сжимается ( 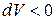), то работа совершается над газом внешними силами и она отрицательна ( ).

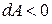При переменном давлении необходимо произвести суммирование элементарных работ от начала до окончания процесса, для этого нужно знать зависимость давления от объема, то есть, должна быть задана функция 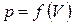. Тогда

.

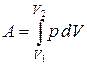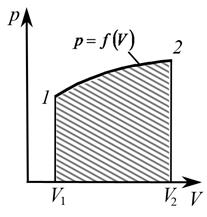
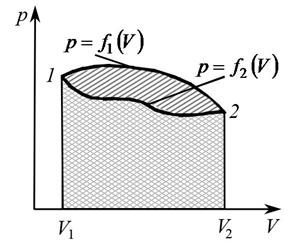
Графически на диаграмме p – V (рис. 4) работа соответствует площади под кривой 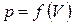между абсциссами V₁ и V₂ (на рисунке заштриховано).

Рис. 4	Рис. 5

Работа по преодолению внешних сил зависит не только от начального и конечного состояний, но и от пути, по которому совершается процесс. Площадь, ограниченная кривой 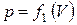(рис. 5), не равна площади, ограниченной кривой 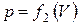, не равны и работы, совершаемые газом при этих процессах.

Как уже отмечалось, молекулы газа обладают кинетической энергией хаотического движения и потенциальной энергией взаимодействия. Сумма этих энергий называется внутренней энергией газа U. В общем случае внутренняя энергия газа зависит от давления, температуры, а значит и от занимаемого газом объема. Поэтому принято говорить, что внутренняя энергия газа является функцией его состояния. Состоянию газа с параметрами p₁, T₁, 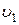соответствует внутренняя энергия U₁, состоянию с параметрами p₂, T₂, 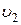– внутренняя энергия U₂. При переходе газа из первого состояния во второе его внутренняя энергия изменяется на величину 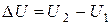. При этом изменение внутренней энергии не зависит от характера процесса, а зависит только от значений энергии в начальном и конечном состоянии.

Закон сохранения энергии является фундаментальным законом природы, имеющим всеобщий характер. Как известно, он формулируется так: энергия не возникает из ничего и не исчезает, она лишь переходит из одного вида в другой в эквивалентных количествах. Применительно к термодинамическим процессам это означает преобразование теплоты в механическую работу.

Если к газу массой m, занимающему при температуре T объем V, подвести при постоянном давлении некоторое количество теплоты 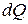, то температура газа повысится на некоторую величину 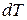, а объем увеличится на величину 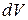. При повышении температуры увеличится кинетическая энергия хаотического движения молекул dK. Увеличение объема приводит к изменению расстояния между молекулами, а значит, к изменению потенциальной энергии газа dH. Увеличивая объем, газ совершает работу по преодолению внешних сил dA. Если больше никаких процессов не происходит, то на основании закона сохранения энергии можно записать

.

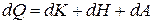Сумма изменений кинетической и потенциальной энергии представляет собой изменение внутренней энергии газа 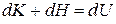. С учетом формулы (8) для работы по преодолению внешних сил можно записать

.

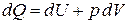(9)

Формула (9) представляет собой первый закон термодинамики: количество теплоты, сообщенное системе, идет на изменение внутренней энергии системы и на совершение системой работы против внешних сил.

Условно принято считать, что при 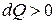теплота сообщается системе, при 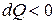теплота отводится (отнимается) от рабочего тела; при 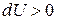внутренняя энергия газа увеличивается, при 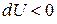внутренняя энергия газа уменьшается; при 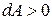система совершает работу против внешних сил (газ расширяется), при 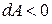работа совершается над системой (газ сжимается).

Так как работа зависит не только от начального и конечного состояния, но и от характера процесса, то из формулы (9) следует, что и количество подводимой или отводимой теплоты зависит от характера процесса.

Первый закон термодинамики можно сформулировать и так: энергия изолированной термодинамической системы остается неизменной независимо от того, какие процессы внутри неё протекают. Следствием из этого закона является следующее утверждение: невозможно создать вечный двигатель первого рода, то есть действующую машину, которая совершала бы работу без затраты энергии.

Теплоемкость газов

Чтобы повысить температуру вещества необходимо сообщить ему определенное количество тепла.

Удельной теплоемкостью называется физическая величина, численно равная количеству теплоты, которое необходимо подвести в единице количества вещества, чтобы повысить его температуру на один градус Кельвина:

.

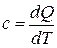В зависимости от выбранной единицы количества вещества удельная теплоемкость может быть массовая с (для нагревания на 1 °К одного кг вещества), молярная с_μ (для нагревания 1 моля вещества) и объемная с^V (отнесенная к 1 м³). Соответственно и единицы измерения теплоемкостей в СИ: массовой – 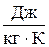, молярной – 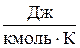, объемной – .

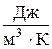Теплоемкость является физическим свойством вещества. Для газов теплоемкость зависит от процесса, при котором осуществляется теплопередача, от способа подвода тепла к газу. Для единицы количества вещества формулу (9) можно записать так:

,

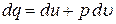где 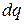– количество тепла, необходимое для нагревания 1 кг на 1 °К;

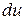– изменение внутренней энергии единицы массы газа;

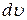– изменение удельного объема газа (объема 1 кг газа).

Тогда

.

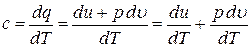Если при подведении к газу теплоты его объем остается постоянным, то есть 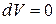, а следовательно и 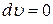, то удельная теплоемкость при постоянном объеме 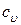будет равна

.

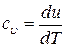(10)

При этом теплота будет затрачиваться только на увеличение внутренней энергии газа, которое определиться из (10) как

.

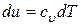То есть при этом будет увеличиваться только температура газа.

Если же при подводе к газу теплоты его давление остается постоянным, то удельная теплоемкость при постоянном давлении 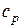определится как

,

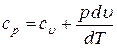(11)

то есть, подводимая теплота затрачивается и на увеличение внутренней энергии газа (увеличение температуры) и на совершение работы по преодолению сопротивления внешних сил (увеличение объема). Таким образом, на увеличение температуры газа на один градус при постоянном давлении необходимо затратить больше теплоты, чем при постоянном объеме. Поэтому (как видно из формулы (11)) теплоемкость при постоянном давлении 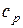больше, чем теплоемкость при постоянном объеме 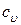. Разницу между этими теплоемкостями можно оценить следующим образом. Вспомним уравнение состояния идеального газа (2)

.

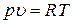Продифференцируем его при постоянном давлении:

,

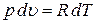откуда получим выражение

.

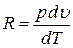Кстати, отсюда становится понятен физический смысл газовой постоянной R. Она показывает, какую работу совершает единица количества газа при нагревании на один градус, если тепло подводилось при постоянном давлении.

Тогда из уравнения (11) мы получаем

.

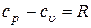(12)

Уравнение (12) называется уравнением Майера.

Для одного киломоля уравнение (12) можно записать как

,

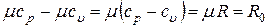где R₀ = 8,31 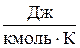– универсальная газовая постоянная.

Таким образом, нагревая газ от температуры T₁ до температуры T₂ при постоянном объеме к нему необходимо подвести количество теплоты

,

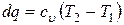а для нагревания при постоянном давлении

.

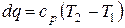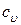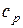Для идеального газа и постоянны, поэтому отношение 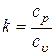тоже постоянно.

Удельная теплоемкость реальных газов (в отличие от идеальных) зависит от давления и температуры. Зависимость от давления незначительна, и ею в практических расчетах можно пренебречь. Но зависимость от температуры существенна. Поэтому при практическом решении теплотехнических задач пользуются понятием средней удельной теплоемкости для некоторого температурного интервала. Значения таких удельных теплоемкостей для различных интервалов температур приведены в справочниках.

Удельную теплоемкость смеси газов определяют путем суммирования количества теплоты, необходимого для нагревания каждого компонента, который содержится в 1 кг смеси, на 1 °К:

,

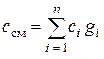где g_i – массовая доля компонента в смеси.