Определение срока ссуды и величины процентной ставки при начислении простых процентов
Различные способы начисления процентов. Простой и сложный проценты
Простые проценты
На предыдущей лекции мы рассматривали, каким образом начисление процентов происходит единственный раз, т.е. в конце (ссудный процент) или в начале (учетный процент) одного интервала начисления. Рассмотрим, каким образом происходит начисление процентов, если первоначальная сумма увеличивается в результате периодического начисления процентов в течение длительного срока, т.е. на протяжении нескольких интервалов.
Пусть задана первоначальная сумма Р и осуществляется ее наращение или рост, т.е. процесс увеличения первоначальной суммы за счет начисления процентов.
S – наращенная (будущая) сумма;
n – количество интервалов начисления процентов;
i – ставка ссудного процента, по которой проценты начисляются в конце каждого отдельного интервала.
Тогда простые ссудные проценты вычисляются следующим образом:
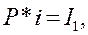
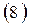
где 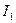 – сумма процентов, начисленных за единицу времени.
– сумма процентов, начисленных за единицу времени.
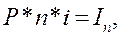
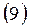
где 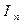 – сумма процентов, начисленных за весь срок (период) начисления, т.е. за все (n) интервалы начисления процентов.
– сумма процентов, начисленных за весь срок (период) начисления, т.е. за все (n) интервалы начисления процентов.
Процесс наращения суммы денежных средств за счет начисления простых процентов выглядит, как арифметическая прогрессия и представлен на рис. 3: P; P + P*i; P + 2*P*i; PV +……+ 3*P*i, и т.д.
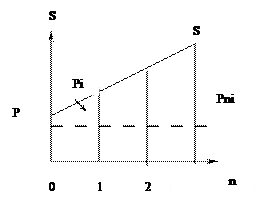 | 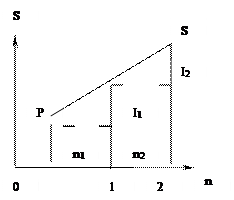 |
Рис. 3. Процесс наращения суммы денежных средств за счет начисления простых процентов
P – первоначальная сумма;
Sn – наращенная сумма;
in – простая процентная ставка;
n – количество интервалов начисления.
Процесс наращения суммы денежных средств за счет начисления простых процентов за n интервалов имеет вид:
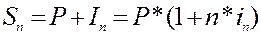
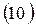
Такой формулой (10) выражается суть практических расчетов, связанных с исчислением:
ü суммы погашения ссуды, предоставленной под простые проценты;
ü размера срочного вклада с простыми процентами.
Пример 4.Банк выдал ссуду 100000 рублей на 2 года под 10% годовых. Определить подлежащую возврату сумму, если простой процент начисляется каждый год, а долг гасится единовременным платежом.
Решение:
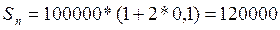 руб.
руб.
Но такого вида простые вычисления встречаются редко. Очень часто ссуды выдаются на срок, который выражен не точным числом лет, а некоторым количеством месяцев или дней. Для подобных расчетов чаще пользуются формулой, где аналитически выражен принцип расчета для случаев, когда годовая ставка задана i, а интервал начисления процентов выражен в днях, реже – в месяцах.
Обозначим срок операции (выраженный в днях) через t. Для перевода срока финансовой операции в доли от года используют уравнивающий знаменатель К, обозначающий продолжительность года, выраженный в тех же единицах, что и t.
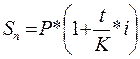
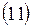
В формуле (11) срок операции 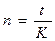
Эта формула используется при:
ü определении абсолютной величины процентов и наращенной суммы в целом при обслуживании вкладов до востребования;
ü обслуживании текущих счетов;
ü расчете суммы долга с процентами при сроке операции менее года и погашении долга единовременным платежом;
ü замене и консолидации платежей;
ü определении размера процентных платежей при составлении планов амортизации (погашения) задолженности.
Определяя продолжительность финансовой операции, принято день выдачи и день погашения ссуды считать за один день.
В зависимости от того, чему принимается равной продолжительность года К (квартала, месяца), выделяют два варианта начисления процентов:
ü точные проценты, определяемые исходя из точного числа дней в году (365 или 366), в квартале (от 89 до 92), в месяце (от 28 до 31);
ü обыкновенные проценты, определяемые исходя из приближенного числа дней в году, квартале, месяце (соответственно 360, 90, 30).
При определении продолжительности периода t, на который выдана ссуда, также возможны два варианта:
ü принимается в расчет точное число дней ссуды (расчет ведется по дням);
ü принимается в расчет приблизительное число дней ссуды (исходя из продолжительности месяца 30 дней).
В зависимости от сочетания t и К, измеренных по-разному, на практике встречаются следующие способы расчетов:
1) точные проценты с точным числом дней–t и К измерены точно–это значит начислить точные проценты с фактическим сроком операции.
Для упрощения процедуры расчета точного числа дней (t) пользуются специальными таблицами или специальными компьютерными программами (такими таблицами в зарубежных странах пользовались до перехода к всеобщей компьютеризации банковских расчетов, т.е. до начала XXI века). Одна таблица составлялась для обычного года, вторая для високосного, в них все дни в году были последовательно пронумерованы: из номера дня окончания операции вычитают день ее начала. Обычно такой способ расчетов обозначается 365/365 и применяется в англосаксонских странах (Великобритания, США);
2) обыкновенные проценты с точным числом дней–t измерено точно, a К–приближенно.Такой способ иногда называется банковским и используется для вычисления ссудных процентов с фактическим сроком операции. Поскольку при вычислении знаменатель больше, чем при расчетах в случае 1, т.е. 360, то размер начисленных процентов при прочих равных условиях также будет несколько большим, чем применение точных процентов. Заметим, что при числе дней ссуды, превышающем 360, данный способ приводит к тому, что сумма начисленных процентов будет больше, чем предусматривается годовой ставкой. Например, если t = 364, то n = 364/360 = 1,011 . Такой способ обычно обозначают 365/360, и используют в таких странах, как Бельгия, Франция и др.);
3) обыкновенные проценты с приближенным числом дней–t и К измерены приближенно. Этот способ применяется для вычисления ссудных процентов с приближенным сроком операции, при некоторых видах расчетов с населением, например при промежуточных расчетах и обозначают как 360/360 (Германия, Дания, Швеция).
Рассмотрим на конкретном примере, как начисляют проценты разными способами.
Пример 5. Ссуда в размере 60000 рублей выдана 12 марта 2012 года с погашением 15 августа того же года под 32% годовых.
Рассчитать различными способами сумму к погашению, если начисляются простые проценты. Предварительно определим число дней ссуды: точное – 156 дней (228-72), приближенное - 153 дней (18 дней марта (30-12) + 120 (по 30 дней четырех месяцев: апрель, май, июнь, июль) + 15 дней августа). Год високосный, значит число дней в году равно 366.
Решение:
1. Точные проценты с точным числом дней ссуды (365/365):
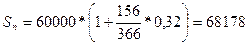 руб.
руб.
2. Обыкновенные проценты с точным числом дней ссуды (365/360):
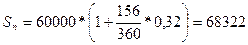 руб.
руб.
3. Обыкновенные проценты с приближенным числом дней ссуды (360/360):
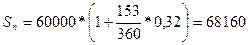 руб.
руб.
Определение срока ссуды и величины процентной ставки при начислении простых процентов
При разработке условий контрактов или их анализе возникает необходимость в решении ряда вторичных задач – определении срока ссуды или размера процентной ставки в том или ином ее виде при всех прочих заданных условиях.
Срок ссуды.Необходимые для расчета продолжительности ссуды в годах и днях формулы получим из формул (10) и (11), решив их относительно n:
срок в годах
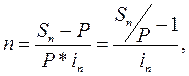
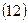
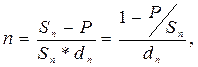
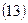
срок в днях (напомним, что n = t/K, где К – временная база)
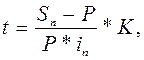
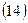
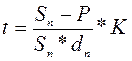
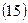
Пример 6.Какова должна быть продолжительность ссуды в днях для того, чтобы долг, равный 1 млн. рублей, вырос до 1,2 млн. рублей при условии, что начисляются простые проценты по ставке 25% годовых (К = 365)?
Решение:
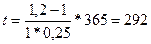 дня
дня
Величина процентной ставки. Необходимость в расчете процентной ставки возникает при определении финансовой эффективности операции и при сравнении контрактов по их доходности в случаях, когда процентные ставки в явном виде не указаны.
Необходимые для расчета величины процентной ставки формулы получим также из формул (10) и (11) , решив относительно i и d:
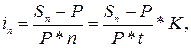
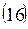
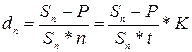
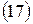
Пример 7.В контракте предусматривается погашение обязательства в сумме 110000 рублей через 120 дней. Первоначальная сумма долга – 90000 рублей. Необходимо определить доходность ссудной операции для кредитора в виде годовой ставки процента и учетной ставки (К = 360).
Решение:
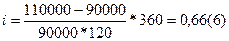 ;
;
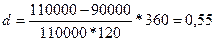
Иногда размер дисконта фиксируется в договоре в виде процента скидки (общей учетной ставки) за весь срок ссуды – d’. В этом случае
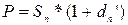
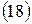
Имея в виду, что P = S/(1 + n*i), находим годовую ставку наращения
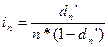
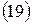
Годовая учетная ставка равна:
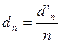
Пример 8.Стороны договорились о том, что из суммы кредита, выданной на 210 дней, удерживается дисконт в размере 12%. Необходимо определить цену кредита в виде годовой ставки простых процентов и учетной ставки (К = 360).
Решение:
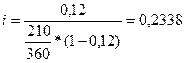 ;
;
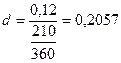
Эквивалентность ставок. Две ставки называются эквивалентными, если при одинаковой первоначальной сумме Р и при одинаковом периоде начисления n они приводят к одинаковой наращенной сумме S.
Если срок финансовой операции выражен в днях или месяцах, а ставка задана годовая, то формулы преобразуются так:
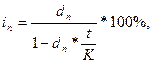
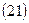
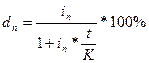
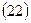
и используются для точных процентов с фактическим сроком операции или обыкновенных процентов с приближенным сроком операции.
Пример 9. Доходность по дисконтной ценной бумаге со сроком обращения 3 месяца оценена в виде дисконтной ставки, равной 100% годовых, а доходность размещения средств на 3-месячный депозит – 120% годовых. Сравнить эффективность этих операций.
Решение:
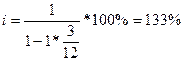
Выгоднее первая финансовая операция, т.к. 133% > 120%
Сложные проценты
Дата добавления: 2017-02-13; просмотров: 7941;










