Начисление сложных процентов
В финансовой практике значительная часть расчетов ведется с использованием сложных процентов.
Принципиальное отличие сложных процентов от простых в том, что база для исчисления процентного платежа (дисконта) меняется на протяжении всего срока финансовой операции за счет периодического присоединения (снятия) начисленного ранее дохода (скидки), в то время как база при использовании простых процентов остается неизменной.
Наращение по сложным процентам можно представить как последовательное реинвестирование средств, вложенных под простые проценты на один период начисления.
Процедуру присоединения начисленных процентов к сумме, которая послужила базой для их начисления называют капитализацией процентов или реинвестированием.
Из-за постоянного роста базы вследствие реинвестирования процентов рост первоначальной суммы денежных средств осуществляется с ускорением. График начисления простых и сложных процентов представлен на рис. 4.
 |
|
 |
Рис. 4. График начисления простых и сложных процентов
Как правило, сложные проценты применяются в средне- и долгосрочных финансовых операциях. Но в любом случае, если начисленные проценты (например, по вкладу) капитализируются, расчеты итоговой наращенной суммы следует вести по формулам сложных процентов, а также при:
ü исчислении возросшей на проценты суммы задолженности, если проценты начисляются и присоединяются к основной сумме долга;
ü неоднократном учете ценных бумаг (учете и переучете на одинаковых условиях);
ü определении арендой платы при лизинговом обслуживании;
ü оценке бескупонных облигаций;
ü определении изменения стоимости денег под влиянием инфляции;
ü дисконтировании денежных сумм за ряд периодов времени в простом проектном анализе.
Исчисление эффективности операций, по которым проценты выплачиваются(не капитализируются), следует вести также по формуле сложного процента исходя из возможности реинвестирования дохода на прежних условиях.
В практике при инвестировании денежных средств в краткосрочные депозиты иногда прибегают к неоднократному последовательному повторению наращения по простым процентам в пределах заданного общего срока, т.е. к реинвестированию полученных на каждом этапе наращения средств. Наращенная сумма для всего срока составит в этом случае
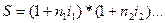
где i – ставки, по которым производится реинвестирование.
Если периоды начисления и ставки не изменяются во времени, то формула имеет вид:
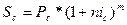 ,
, 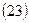
где m – количество реинвестиций.
Пример 10.Смирнов Е.Н. положил 100000 рублей 1 марта на месячный депозит под 20% годовых. Какова наращенная сумма, если операция повторяется три раза?
Решение:
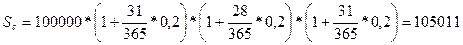 руб.
руб.
Если начисляются точные проценты с точным числом дней
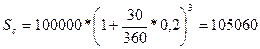 руб.
руб.
Если обыкновенные проценты с приближенным числом дней.
Найдем формулу для расчета наращенной суммы при условии, что проценты начисляются и капитализируются один раз в году (годовые проценты), т.е. применяется сложная годовая ставка наращения. Для записи формулы наращения применим те же обозначения, что и в формуле наращения по простым процентам:
Рс – первоначальный сумма долга (ссуды, кредита и т.д.);
Sс –наращенная сумма;
п – интервал начисления (число лет наращения).
Ставку наращения по сложным процентам обозначим как iс. В тех случаях, когда одновременно речь идет о простых и сложных процентах, для ставки простых процентов будем применять подстрочный индекс «п».
Очевидно, что в конце первого года проценты равны величине Pi, а наращенная сумма составит Р + Pi = Р*(1 + i).
К концу второго года она достигнет величины Р*(1 + i) + Р*(1 + i) = Р(1 + i)2 и т.д.
В конце i-го года наращенная сумма будет равна
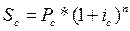
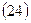
Выражение (1 + iс)n называют коэффициентом (множителем) наращения по сложным процентам. Точность расчета множителя в практических расчетах определяется допустимой степенью округления наращенной суммы (до последней копейки, рубля, тысячи и т.д.).
Пример 11.Какой величины достигнет долг, равный 100000 рублей, через пять лет при росте по сложной ставке 15,5% годовых?
Решение:
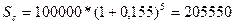 руб.
руб.
Как видим, величина множителя наращения зависит от двух параметров – i и n.Следует отметить, что при большом сроке наращения даже небольшое изменение ставки заметно влияет на величину множителя. В свою очередь очень большой срок приводит к устрашающим результатам даже при небольшой процентной ставке.
Данная формула получена для годовой процентной ставки и срока, измеряемого в годах. Однако ее можно применять и при других периодах начисления. В этих случаях i – ставка за период начисления, n–число таких периодов.
Например, если i – ставка за полугодие, то n – число полугодий и т.д.
Переменные ставки.Формула сложного процента предполагает постоянную ставку на протяжении всего срока начисления процентов. Неустойчивость кредитно-денежного рынка заставляет модернизировать «классическую» схему, например с помощью применения плавающих ставок. Естественно, что расчет на перспективу по таким ставкам весьма условен. Иное дело расчет постфактум. В этом случае, а также тогда, когда значения переменных ставок фиксируются в контракте, общий множитель наращения определяется как произведение частных множителей
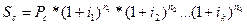 ,
, 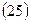
где i1, i2, ik –последовательные во времени значения ставок;
n1, n2, nk–периоды, в течение которых применяются соответствующие ставки.
Пример 12. Срок ссуды – 5 лет, договорная процентная ставка – 12% годовых плюс маржа 0,5% в первые два года и 0,75% – в оставшиеся. Множитель наращения в этом случае составит:
Решение:
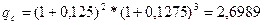
Начисление процентов при дробном числе лет.Часто срок для начисления процентов не является целым числом. В правилах ряда коммерческих банков для некоторых операций в этих случаях проценты начисляются только за целое число лет (или других периодов начисления). В большинстве же случаев учитывается полный срок. При этом применяются два метода. Согласно первому, назовем его общим,расчет ведется непосредственно по формуле 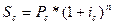 . Второй, смешанный,метод предполагает начисление процентов за целое число лет по формуле сложных процентов и по формуле простых процентов за дробную часть периода:
. Второй, смешанный,метод предполагает начисление процентов за целое число лет по формуле сложных процентов и по формуле простых процентов за дробную часть периода:
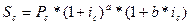 ,
, 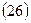
где а + b = n
а – целое число периодов;
b – дробная часть периода.
При выборе метода следует иметь в виду, что множитель наращения по смешанному методу оказывается несколько больше, чем по общему методу, так как для n < 1 справедливо соотношение 1 + n*i > (1 + i)n. Наибольшая разница наблюдается при b=1/2.
Пример 13. Кредит в размере 3 млн. рублей выдан на три года и 160 дней (n = 3, 160/365 = 3,4384 года) под 16,5% сложных годовых. Найти сумму долга:
Решение:
Общий метод:
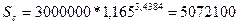 руб.
руб.
Смешанный метод:
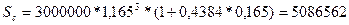 руб.
руб.
Дата добавления: 2017-02-13; просмотров: 3516;










