Основные задачи и понятия сопротивления материалов

12 3

В результате механического взаимодействия с окружающей средой материальный объект (твердое тело) приобретает возможность двигаться или деформироваться (изменять размеры и форму). Движение абсолютно твердых тел и материальных точек нами уже изучено. Теперь будем рассматривать деформирование твердых тел, т. е. изменение расстояний между двумя любыми точками твердого тела. Одним из разделов механики деформируемого твердого тела является сопротивление материалов - наука, в которой изучаются инженерные методы расчетов на прочность, жесткость и устойчивость.

Прочность — это способность конструктивного элемента выдерживать эксплуатационную нагрузку без разрушения.

Жесткость — это способность элемента конструкции выдерживать эксплуатационные нагрузки с незначительными изменениями размеров и формы, не приводящими к нарушению функциональной пригодности изделия.

Устойчивость — это способность элемента конструкции выдерживать эксплуатационную нагрузку с сохранение его первоначальной формы упругого равновесия.

Сопротивление материалов базируется на результатах экспериментальных исследований, абстракциях и допущениям. Расчеты выполняются с использованием методов теоретической механики, математики и других наук.

Способность элемента конструкции деформироваться по понятным причинам будет определяться его геометрической формой, материалом и внешними нагрузками, поэтому основные допущения и абстракции в сопротивлении материалов связаны с этими понятиями.

Элементы конструкций машин и механизмов зачастую имеют довольно сложную форму. Среди всего многообразия геометрических форм объектов, которые подлежат расчету на прочность, жесткость и устойчивость, в той или иной степени приближенности к истине можно выделить три их группы: стержни, оболочки, массивы.

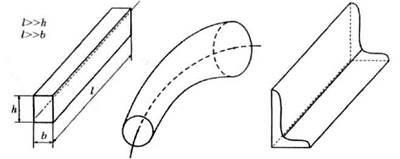
Рисунок 1.

Стержнем называют такое тело, у которого один размер существенно больше двух других. Больший размер называют длиной стержня, меньшие размеры характеризуют поперечное сечение стержня, которое получают в результате сечения плоскостью, перпендикулярной оси стержня. Ось стержня — это геометрическое место точек центров тяжести поперечных сечений. Стержни классифицируют следующим образом: по форме оси — прямолинейные, криволинейные; по форме поперечного сечения — круглые, прямоугольные и др.; по размерам поперечного сечения — стержни постоянного поперечного сечения и стержни переменного поперечного сечения. Различные виды стержней приведены на рисунке 1.

Оболочкой называют такое тело, у которого один размер (толщина) существенно меньше двух других. Оболочка образуется двумя близко расположенными поверхностями. Поверхность, проведенную через середины толщин, называют срединной поверхностью. Оболочки классифицируют так: по форме срединной поверхности — на сферические, конические, цилиндрические, плоские (чаще их называют пластинками); по величине толщины — на оболочки постоянной толщины и оболочки переменной толщины; по форме в плане – на прямоугольные (когда часть произвольной оболочки выделена прямоугольным цилиндром), круглые (когда часть оболочки выделена круговым цилиндром) и дp. Виды оболочек приведены на рисунке 2.

Массивом называют тело, у которого три поперечных размера соизмеримы. Массивы классифицируют по форме (например, параллелепипед, цилиндр и др.)

В курсе технической механики в разделе «Сопротивление материалов» в качестве обьекта будем рассматривать только стержни. Как отмечалось выше, стержни характеризуются длиной, формой оси и поперечным сечением. Поперечное сечение является одним из основных факторов, определяющих способность стержня деформироваться, поэтому сначала изучим основные геометрические характеристики плоских поперечных сечений.

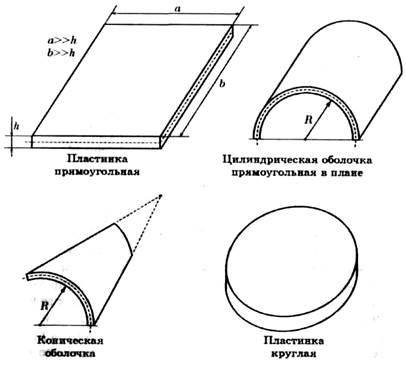
Рисунок 2.

Основные гипотезы (допущения) о материале

Конструктивные элементы машин и механизмов изготавливаются из различных материалов: металлов, сплавов, дерева, полимеров и др. Как правило, материалы имеют неоднородности, несплошности и другие дефекты. Атомистическая теория строения вещества вообще говорит о дискретной структуре. Математическое описание макрообъектов с учетом этих особенностей затруднено. В связи с этим в сопротивлении материалов приняты гипотезы.

Гипотеза о сплошности материала предполагает, что материал заполняет форму тела сплошь, т.е. в любом элементарном объеме, выделенном в пределах тела, содержится вещество.

Гипотеза об однородности материала предполагает, что в любом элементарном объеме, выделенном в пределах тела, содержится одно и тоже вещество, обладающее одинаковыми свойствами. Свойство вещества определяются с использованием макрообъектов.

Гипотеза об изотропности предполагает, что свойство материала в различных направлениях одинаковы. Анизотропные материалы – это материалы, свойства которых зависят от направления. Пример такого материала – дерево: его свойства вдоль волокон отличаются от свойств поперек волокон.

Гипотеза об идеальной упругости предполагает, что изменения размеров и формы тела, которые вызваны внешними силами, исчезают после снятия нагрузки, т. е. тело восстанавливает свою первоначальную форму.

Гипотеза о пропорциональной (линейной) зависимости предполагает, что все изменения размеров и формы тела, вызванные внешней нагрузкой, линейно зависят от величины этой нагрузки.

Тема: «Понятие о центральном растяжении и сжатии»

Растяжение — это такой вид деформирования, когда в поперечном сечении возникает только продольная сила. Растяжение характерно только для прямолинейных стержней (они могут быть и переменного поперечного сечения), которые нагружены силами, приложенными в центрах тяжести поперечных сечении и направленными вдоль продольной оси стержня.

При растяжении (сжатии) прямого бруса в его поперечных сечениях возникает только один внутренний силовой фактор — продольная сила, обозначаемая или .

Прямые брусья, работающие на растяжение или сжатие, часто называют стержнями.

Продольные силы, соответствующие деформации растяжения, условимся считать положительными, а сжатия - отрицательными. При растяжении продольная сила направлена от сечения, а при сжатии — к сечению.

Для того чтобы брус работал на растяжение (сжатие), равнодействующая внешних сил, приложенных во одну сторону от любого поперечного сечения бруса, должна быть направлена вдоль его оси. Только при этом условии все внутренние силовые факторы, кроме продольной силы, будут равны нулю.

Модуль и направление (знак) продольной силы определяются из уравнения равновесия, составленного для отсеченной (оставленной после проведения сечения) части бруса.

Продольная сила в произвольном поперечном сечении бруса численно равна алгебраической сумме проекций на его продольную ось Oz всех внешних сил, приложенных к оставленной части.

Рассмотрим стержень, изображенный на рисунке 1.

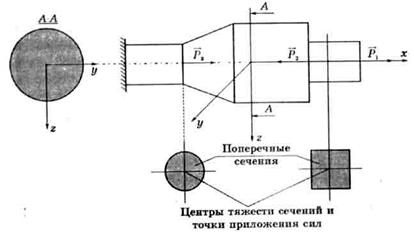
Рисунок 1.

Проведем произвольное сечение А-А. Мысленно отбросим правую часть. В сечении, принадлежащем левой части, введем систему координат xyz (ось x направлена вдоль оси стержня от рассматриваемого сечения; оси y, z – главные центральные оси инерции сечения).

Продольная сила в общем случае не равна нулю, так как внешние силы направлены вдоль оси стержня (с ней совпадает ось х).

Поперечные силы и всегда будут равны нулю, там как оси y и z перпендикулярны продольной оси стержня, вдоль которой направлены внешние силы.

Крутящий момент всегда равен нулю, поскольку внешние силы действуют вдоль оси х и относительно этой оси момента не создают.

Изгибающие моменты и также будут нулевыми из-за того, что линия действия внешних сил (ось х ) пересекается с главными центральными осями инерции.

Таким образом, если прямолинейный стержень нагружен системой сил, действующей вдоль его оси, то из шести возможных внутренних силовых факторов будет возникать один — продольная сила.

Тема: «Продольные силы и нормальные напряжения. Построение эпюр»

Продольной силой в поперечном сечении бруса называется равнодействующая внутренних нормальных сил, возникающих в этом сечении.

В тех случаях, когда продольные силы в различных поперечных сечениях бруса неодинаковы, закон их изменения по длине бруса удобно представить в виде графика, называемого эпюрой продольных сил. Аргументом при построении этого графика является координата поперечного сечения бруса (z), а функцией - продольная сила (N).

Таким образом, эпюра продольных сил - это график функции . Далеко не всегда можно составить выражение указанной функции, справедливое при всех значениях координаты z (для всего бруса). Приходится разбивать брус на участки, для каждого из которых будет свое выражение функции .

Эпюру продольных сил строят в первую очередь для того, чтобы использовать ее при расчете бруса на прочность; она дает возможность найти наибольшие значения продольных сил и положение сечений, в которых они возникают.

При растяжении (сжатии) бруса в его поперечных сечениях возникают только нормальные напряженна. Равнодействующая соответствующих элементарных сил - продольная сила N - может быть найдена с помощью метода сечений. Для того чтобы иметь возможность определить нормальные напряжения при известном значения продольной силы, необходимо установить закон их распределения по поперечному сечению бруса.

Эта задача решается на основе гипотезы плоских сечений (гипотезы Я. Бернулли), которая гласит: сечения бруса, плоские и нормальные к его оси до деформации, остаются плоскими и нормальными к оси и при деформации.

При растяжении бруса (изготовленного, например, для большей наглядности опыта из резины), на поверхности которого нанесена система продольных и поперечных рисок, можно убедиться, что риски остаются прямолинейными и взаимно перпендикулярными, изменяются лишь расстояния: между поперечными рисками несколько увеличиваются, а между продольными - уменьшаются.

Описанный опыт можно рассматривать как подтверждение гипотезы плоских сечений; при этом предполагают, что внутри бруса деформации имеют тот же характер, что и на его поверхности.

Представим себе, что брус состоит из бесконечно большого числа продольных элементов, имеющих бесконечно малые («точечные») поперечные сечения. Эти элементы здесь и в дальнейшем будем, условно называть волокнами.

Из гипотезы Бернулли следует, что все волокна в рассматриваемом случае деформируются одинаково. При однородном материале равным деформациям соответствуют одинаковые напряжения. Таким образом, приходим к заключению, что при растяжении (сжатии) бруса нормальные напряжения распределены по его поперечному сечению равномерно.

Для нормальных напряжений принимают то же правило знаков, что и для продольных сил, т. е. при растяжении считают напряжения положительными.

Фактически распределение напряжений в сечениях бруса, примыкающих к месту приложения внешних сил, зависит от способа приложения нагрузки и может быть неравномерным. Экспериментальные и теоретические исследования показывают, что это нарушение равномерности распределения напряжений идет местный характер. В сечениях бруса, отстоящих от места нагружения на расстоянии, примерно равном наибольшему из поперечных размеров бруса, распределение напряжений можно считать практически равномерным (рисунок 1).

Рассмотренное положение является частным случаем принципа Сен-Венана, который можно сформулировать следующим образом: распределение напряжений существенно зависит от способа приложении внешних сил лишь вблизи мести нагружения.

В частях, достаточно удаленных от места приложения сил, распределение напряжений практически зависит только от статического эквивалента этих сил, а не от способа их приложении.

Таким образом, применяя принцип Сен-Венана и отвлекаясь от вопроса о местных напряжениях, имеем возможность не интересоваться конкретными способами приложения внешних сил.

В местах резкого изменения формы и размеров поперечного сечения бруса также возникают местные напряжения. Это явление называют концентрацией напряжений.

Рисунок 1. Рисунок 2.

В тех случаях, когда нормальные напряжения в различных поперечных сечениях бруса неодинаковы, целесообразно показывать закон их изменения по длине бруса в виде графика - эпюры нормальных напряжений.

При построении эпюр необходимо придерживаться следующих правил:

- ось эпюры всегда проводят параллельно оси стержня;

- значения внутренних силовых факторов откладывают на оси ординат, перпендикулярной оси эпюры в масштабе;

- эпюру заштриховывают линиями, перпендикулярными оси;

- в характерных точках эпюры проставляют численные значения, на поле эпюры в круге ставят знак.

Отметим, что в пределах стержня можно выделить зоны, где внутренние силовые факторы описываются одной и той же закономерностью; которая определяется действующей нагрузкой на отброшенной части. Эти зоны будем называть участками. Границами участков будут служить сечения, в которых происходит изменение закона внешней нагрузки или изменение направления продольной оси.

Эпюры внутренних силовых факторов рекомендуется строить в следующем порядке:

1. Определить все внешние силы. Необходимо помнить, о наличии реакций связей.

2. Разбить стержень на участки.

3. Используя метод сечений, записать аналитические выражения для всех внутренних силовых факторов на всех участках.

4. Построить эпюры внутренних силовых факторов.

5. Выполнить проверку.

Задача.

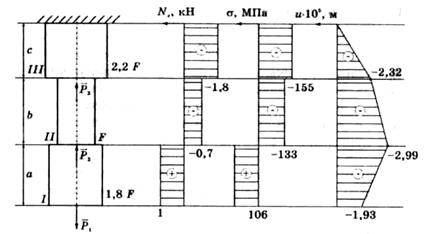
Построить эпюру продольных сил для ступенчатого стержня, нагруженного сосредоточенными силами: Дано: .

Решение.

1. Используя принцип освобождаемости, вместо жесткой заделки прикладываем реакцию R, которую в данной задаче можно не определять.

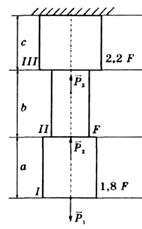
2. Разбиваем стержень на участки: I — часть стержня длиной а; II — часть стержня длиной b; III — часть стержня длиной с.

3. Рассматриваем участок I. В пределах участка проводим произвольное сечение, задаем его координату х (начало отсчета — от начала стержня). Считая мысленно отброшенной нижнюю часть, определяем численное значение продольной силы как величину проекции силы Р₁ на продольную ось х. Значение продольной силы будет со знаком «плюс», так как сила P₁ направлена от рассматриваемого сечения:

Повторив п. 3 для участков II и III, получим

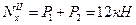
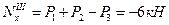
Сила дает отрицательную продольную силу, так как она направлена к сечению.

5. Строим эпюру продольных сил.

6. Выполняем проверку правильности построения эпюры продольных сил по скачкам, величина скачка на эпюре должна быть равна величине сосредоточенной силы, действующей в этом сечении.

Тема: «Напряжения в наклонных сечениях бруса. Деформации при растяжении сжатии»

Через точку можно провести бесчисленное множество различно ориентированных площадок, и, конечно, в общем случае нет никаких оснований предполагать, что возникающие на них напряжения одинаковы.

Совокупность нормальных и касательных напряжений, возникающих на всем бесчисленном множестве площадок, которые можно провести через данную точку, характеризует напряженное состояние в этой точке.

Исследовать напряженное состояние в данной точке - это значит получить зависимости, позволяющие определить напряжения, возникающие в любой проведенной через нее площадке. Для решения этой задачи надо знать напряжения по любым трем взаимно перпендикулярным площадкам, проведенным через исследуемую точку. Эти площадки и возникающие на них напряжения называют исходными. При исследовании напряженного состояния в различных точках прямого бруса в любом случае его, нагружения исходными являются напряжения, возникающие на площадках, соответствующих поперечному и двум продольным сечениям, проходящим через рассматриваемую точку. При растяжении (сжатии) прямого бруса в поперечных сечениях возникают только нормальные напряжения, определяемые по формуле

.

Индекс z показывает, что это напряжение возникает на площадке, нормаль к которой параллельна оси z.

Для исследования напряженного состояния мысленно вырежем вокруг произвольной точки бруса бесконечно малый параллелепипед (рисунок 1). В дальнейшем такие элементарные параллелепипеды будем называть элементами или частицами.

Рисунок 1. Рисунок 2.

В рассматриваемом случае совершенно безразлично, где именно вырезать эту частицу, так как напряженное состояние всех точек бруса одинаково - однородное напряженное состояние. Для того чтобы выделенный элемент находился в равновесии, следует приложить к его граням внутренние силы, заменяющие действие отброшенных частей тела (бруса) на оставленную. Обращаем внимание, что здесь мы поступаем в полном соответствии с требованиями метода сечений, но если ранее при определении продольных сил было достаточно рассечь брус плоскостью, совпадающей с интересующим нас поперечным сечением, то новая задача — исследование напряженного состояния — потребовала иного применения этого метода: элемент вырезан шестью сечениями.

Выделенный элемент (модель напряженной точки) изображен отдельно на рисунке 1, б. На его гранях, совпадающих с плоскостями поперечного сечения бруса, возникают нормальные напряжения, остальные четыре грани от напряжений свободны.

Мысленно разрежем выделенный из бруса элемент плоскостью, нормаль к которой составляет произвольный угол α с осью z. Это наклонное сечение показано на рисунке 2, а. На рисунке 2, б отдельно изображена бесконечно малая трехгранная призма, отсеченная от элементарного параллелепипеда.

На ее наклонной грани возникают напряжения и , подлежащие определению.

Составом уравнения равновесия элементарной призмы. При этом для разделения неизвестных выберем оси проекций, как показано на рисунке 3. Обращаем внимание внимание, что уравнения равновесия составляются для сил, а не для напряжений, т.е. каждое из напряжений следует умножить на площадь грани, на которой оно возникает.

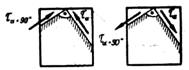
Рисунок 3. Рисунок 4.

Пусть площадь наклонной грани , тогда возникающие на ней силы равны и .

Напряжение возникает на грани, имеющей площадь ; соответствующая сила равна .

Составляем уравнения равновесия;

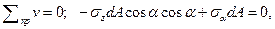
откуда

откуда

или

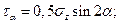
Сделаем некоторые выводы из подученных результатов.

Наибольшее нормальное напряжение возникает в поперечном сечении бруса

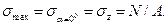
Наибольшее касательное напряжение возникает на площадке, наклоненной под углом 45° к оси бруса, и равно половине нормального напряжения, возникающего в соответствующей точке поперечного сечения:

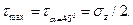
Из формулы вытекает равенство (по абсолютному значению) касательных напряжений, возникающих на взаимно перпендикулярных площадках:

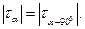
Это равенство носит название закона парности касательных напряжений.

Касательные напряжения, возникающие на взаимно перпендикулярных площадках, направлены всегда оба к ребру или от ребра пересечения этих площадок.

Задача.

Для стержня по заданным силам при известном соотношении площадей по участкам определить размеры поперечного сечения, если известны допускаемые напряжения материала, который по-разному сопротивляется растяжению и сжатию. Построить эпюры напряжений и перемещений. Заданы величины: , ; ;

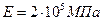
Решение.

Из условия задачи ясно, что необходимо выполнить проектировочный расчет с использованием условия прочности, которое должно быть записано в опасной сечении. Для выбора опасного сечения нужно знать закон распределения по длине стержня продольных сил при заданном соотношении площадей.

1. Строим эпюру продольных сил:

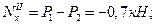
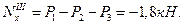
2. Выбираем опасное сечение. Поскольку допускаемые напряжения на растяжение и сжатие различны, будем использовать условия прочности для растянутой и сжатой зон автономно.

Растянутым является только I участок, поэтому для него записываем

откуда находим

Сжатыми являются II и III участки. Записываем для них напряжения по модулю

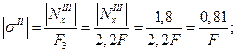
Сравнение этих величий показывает, что напряжение на III участке больше, поэтому условие прочности для сжатой зоны будет иметь вид

Отсюда находим другое значение площади:

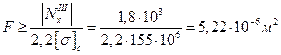
Из двух полученных значений площади F необходимо выбрать большее, т. е. то, которое удовлетворяет и одному, и другому условию. Итак, это .

3. Определяем напряжения по участкам и строим эпюру:

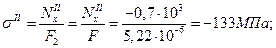
Итак, напряжения на I и II участках меньше допускаемых, а на III участке равны допускаемым, так как именно из условия равенства максимальных напряжений третьего участка допускаемым напряжениям определена площадь поперечного сечения.

4. Строим эпюру перемещений. Ранее мы отметили, что при постоянных по длине стержня площади поперечного сечения и продольной силе, перемещения являются линейной функцией координаты сечения т. е. для построения эпюры перемещений необходимо для каждого участка определить перемещения двух сечений.

Верхнее сечение III участка закреплено, поэтому его перемещение равно нулю.

Определяем перемещение конца III участка (отсчет ведем сверху):

а поскольку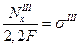

то

Перемещение начала II участка совпадает с перемещением конца III. Находим перемещение конца II участка:

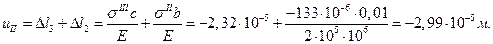
Перемещения конца II и начала I участков одинаковы. Вычисляем перемещение конца I участка:

Строим эпюру перемещений.

Тема: «Закон Гука. Модуль продольной упругости. Коэффициент Пуассона. Испытания материалов»

Продольную и поперечную деформации называют линейными деформациями (общее наименование).

Для подавляющего большинства конструкционных материалов с достаточной для практики точностью можно считать, что в известных пределах нагружения между продольной деформацией и соответствующим (действующим в ее направлении) нормальным напряжением существует прямо пропорциональная (линейная) зависимость.

Это положение носит название закона Гука и записывается в виде

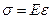
Коэффициент пропорциональности называют модулем предельной упругости (другие названия: модуль нормальной упругости; модуль упругости; модуль упругости 1-го рода; модуль Юнга). Очевидно, имеет ту же размерность, что и напряжение, т. е. выражается в Па или МПа.

Модуль продольной упругости — физическая постоянная данного материала, характеризующая его жесткость. Чем жестче материал, тем меньше он деформируется при данном напряжении. На рисунке 1 дано графическое представление закона Гука для двух материалов, имеющих различные модули продольной упругости.

Рисунок 1.

Пусть по оси ординат графика принят масштаб (Па/мм), а по оси абсцисс — (1/мм).

Значение модуля продольной упругости найдем из выражения:

или по графику:

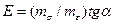
т, е. модуль упругости прямо пропорционален тангенсу угла наклона к оси абсцисс прямой, т. е. графика, изображающего закон Гука.

Опытным путем установлено, что при простом растяжении или сжатии отношение поперечной деформации к продольной - величина постоянная для данного материала. Это отношение, взятое по абсолютному значению, называется коэффициентом поперечной деформации или коэффициентом Пуассона:

.

Значения коэффициента Пуассона для различных материалов находятся в пределах от 0 до 0,5.

Конструктор, выбирая материал для проектируемой детали, а затем рассчитывая ее на прочность (жесткость, устойчивость), должен располагать данными о механических свойствах материала, т. е. его прочности, пластичности и т. п., а также знать значения упругих постоянных — модуля продольной упругости Е и коэффициента Пуассона μ.

Основные механические характеристики, определяемые при испытаниях материалов:

1. Прочность — способность материалу не разрушаясь, воспринимать внешние механические воздействия.

2. Пластичность — способность материала давать значительные остаточные деформации, не разрушаясь.

3. Упругость — способность материала восстанавливать после снятия нагрузок свои первоначальные формы и размеры.

4. Твердость — способность материала сопротивляться проникновению в него другого тела, практически не получающего остаточных деформаций.

Характер нагружения (статическое, динамическое, повторно-переменное) и условия работы деталей машин и инженерных сооружений весьма разнообразны. Располагая сведениями о свойствах материала при определенном виде деформации (например, растяжении) и характере нагружения (например, статическом), судить о его свойствах при других условиях можно лишь весьма приближенно, что в ряде случаев недопустимо. Поэтому механические испытания материалов отличаются большим разнообразием.

По характеру нагружения различают испытания статические, динамические и испытания на усталость (при переменных напряжениях).

По виду деформации различают испытания на растяжение, сжатие, срез, кручение, изгиб. Реже проводят испытания при сложном нагружении, например на совместное действие изгиба и кручения.

Большинство испытаний проводится при нормальной (комнатной) температуре, но для деталей паровых котлов, турбин, реактивных двигателей и т. п. необходимо знать их свойства при высоких температурах.

В некоторых случаях возникает необходимость в испытаниях конструкционных материалов при низких температурах.

Механические испытания проводят на образцах, формы и размеры которых установлены ГОСТами или техническими условиями.

Механические испытания имеют большое значение не только для расчета на прочность, но и для контроля качества материала или выпускаемых изделий. При этом испытаниям могут, подвергаться как специально изготовленные образцы, так и сами изделия (детали или узлы).

Широко применяют механические испытания и в процессе создания новых конструкционных материалов, которые должны, обладать определенными механическими свойствами.

Тема: «Расчеты на срез и смятие заклепочных, штифтовых и шпоночных соединений»

Детали, служащие для соединения отдельных элементов машин или строительных конструкций,— заклепки, штифты, болты и т. п. во многих случаях воспринимают нагрузки, перпендикулярные их продольной оси.

Поперечная нагрузка в указанных деталях возникает, в частности, при растяжении (сжатии) соединяемых элементов. Соответствующие примеры приведены на рисунке 1: а - штифт, б -г заклепка, а — болт, поставленный без зазора; г - шпонка. Такой же характер нагружения соединительных деталей имеет место и при передаче вращающего момента, например в показанном на рисунке 2 соединении шестерни с валом с помощью штифта. Последний при передаче момента от шестерни к валу (или наоборот) несет нагрузку, перпендикулярную его оси.

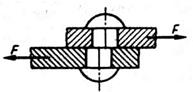
Рисунок 1. Рисунок 2. Рисунок 3

Действительные условия работы рассматриваемых деталей сложны и во многом зависят от технологии изготовления отдельных элементов конструкции и ее сборки.

Практические расчеты этих деталей носят весьма условный характер и базируются на следующих основных допущениях:

1. В поперечном сечении возникает только один внутренний силовой фактор – поперечная сила Q;

2. Касательные напряжения, возникающие в поперечном сечении, распределены по его площади равномерно;

3. В случае если соединение осуществлено несколькими одинаковыми деталями (болтами и т. п.), принимается, что все они нагружены одинаково.

Разрушение соединительных элементов (в случае недостаточной прочности) происходят в результате их перерезывания по плоскости, совпадающей с поверхностью соприкосновенна соединяемых деталей (рисунок 3). Поэтому говорят, что эти элементы работают на срез, и возникающие в их поперечном сечении касательные напряжения также называют напряжениями среза и обозначают .

На основе сформулированных выше допущений получаем следующее условие прочности:

,

где — расчетное напряжение среза, возникающее в поперечном сечения рассчитываемой детали; Q — поперечная сила; при нескольких одинаковых соединительных деталях (F - общая нагрузка соединения, i - число болтов, заклепок и т.п.); А_ср — площадь среза одного болта, заклепки и т. п.; — допускаемое напряжение на срез, зависящее от материала соединительных элементов и условий работы конструкции. В машиностроении при расчете штифтов, болтов, шпонок и т. д. принимают , где - предел текучести материала штифта, болта и др.

Меньшие значения принимают при невысокой точности определения действующих нагрузок и возможности не строго статического нагружения.

Формула является зависимостью для проверочного расчета соединения. В зависимости от постановки задачи она может быть преобразована для определения допускаемой нагрузки или требуемой площади сечения (проектный расчет).

Расчет на срез обеспечивает прочность соединительных элементов, но не гарантирует надежности конструкции (узла) в целом. Если толщина соединяемых элементов недостаточна, то давления, возникающие между стенками их отверстий и соединительными деталями, получаются недопустимо большими. В результате стенки отверстий обминаются и соединение становится ненадежным. В случае если изменение формы, отверстия значительно (при больших давлениях), а расстояние от его центра до края элемента невелико, часть элемента может срезаться (вколоться). Давления, возникающие между поверхностями отверстий и соединительных деталей, принято называть напряжениями смятия и обозначать их . Соответственно расчет, обеспечивающий выбор таких размеров деталей, при которых не будет значительных деформаций стенок отверстий, называют расчетом на смятие. Распределение напряжений смятия на поверхности контакта деталей весьма неопределенно и в значительной степени зависит от зазора (в ненагруженном состоянии) между стенками отверстия и болтом (заклепкой и др.). Расчет на смятие носит условный характер и ведется в предположении, что силы взаимодействия между деталями равномерно распределены по поверхности контакта и во всех точках нормальны к этой поверхности.

Соответствующая расчетная формула имеет вид

Здесь - нагрузка на одну соединительную деталь; - расчетная площадь смятия; - допускаемое напряжение на смятие.

В машиностроении для болтовых, штифтовых и шпоночных соединений принимают: для деталей из малоуглеродистой стали ; для деталей из среднеуглеродистой стали ; для деталей из чугунного литья . Зачастую контактирующие детали изготовлены из различных материалов; в этих случаях при выборе допускаемого напряжения ориентируются на материал той детали, прочность которого меньше.

За расчетную площадь смятия при контакте по плоскости принимают действительную площадь соприкосновения где - размер шпонки в направлении, перпендикулярном плоскости чертежа; при контакте по цилиндрической поверхности принимают площадь проекции поверхности контакта на диаметральную плоскость, т. е. . При различной толщине соединяемых деталей в расчетную формулу следует подставлять .

Неразъемные соединения деталей машин и строительных конструкций имеют две основные разновидности: заклепочные и сварные.

Неразъемные эти соединения называют потому, что для их разборки необходимо разрушить соединительные элементы – заклепки, сварные швы.

Зависимость для проверочных расчетов имеет следующий вид:

а) на срез