Метод, основанный на разложении решения в ряд Тейлора
Отличие этого метода от предыдущих состоит в том, что исходное дифференциальное уравнение не надо представлять в разностном виде. Искомое решение разбивают на ряд участков (число их в пределе должно стремиться к бесконечности), на каждом из которых оно представлено рядом Тейлора. Затем эти участки припасовывают (сшивают).
Алгоритм припасовывания описывается системой линейных алгебраических уравнений, имеющей, как правило, сильно разреженную матрицу. Именно эта матрица определяет пересчет краевых условий для каждого из участков. Решение же самой системы линейных алгебраических уравнений можно проводить методом Гаусса или другими методами, являющимися частными случаями последнего.
По-прежнему будем рассматривать систему линейных алгебраических уравнений с сильно разреженной матрицей, задающую алгоритм пересчета краевых условий от предыдущего участка к последующему в общем виде и представляемую формулой
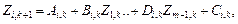
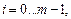
 (7)
(7)
где m — порядок дифференциального уравнения; K — число участков припасовывания или дискретных значений переменных, вводимое для численного решения задачи; i — порядок производной или номер краевого условия; k — номер участка припасовывания.
 — дискретные значения искомого решения, записываемые в матрицу Z. В частном случае, когда заданы все
— дискретные значения искомого решения, записываемые в матрицу Z. В частном случае, когда заданы все 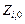 (начальные условия задачи Коши), формула (7) служит для их пересчета (алгоритм пересчета может быть разным) в конечные значения Z(x) на участке припасовывания (или начальные значения последующего участка припасовывания). Вместо начальных условий могут быть заданы краевые условия. Отличие краевых условий от начальных условий состоит в том, что какая-то часть начальных условий задана в начале, а другая — в конце интервала изменения переменных.
(начальные условия задачи Коши), формула (7) служит для их пересчета (алгоритм пересчета может быть разным) в конечные значения Z(x) на участке припасовывания (или начальные значения последующего участка припасовывания). Вместо начальных условий могут быть заданы краевые условия. Отличие краевых условий от начальных условий состоит в том, что какая-то часть начальных условий задана в начале, а другая — в конце интервала изменения переменных.
Описанный ниже алгоритм справедлив для дифференциального уравнения 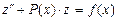 с заданными начальными условиями
с заданными начальными условиями 
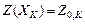 (или
(или 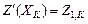 ).
).
Для участка с номером k справедливы следующие соотношения:
 (8)
(8)
 значения
значения 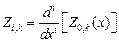 вычислены в точке
вычислены в точке 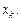
Тогда
 (9)
(9)
где 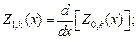
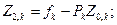
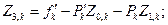 (10)
(10)
 (11)
(11)
Учитывая, что 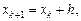
 и подставляя в (8) и (9) выражения (10), (11), получаем
и подставляя в (8) и (9) выражения (10), (11), получаем
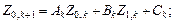
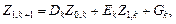 (12)
(12)
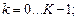
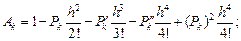
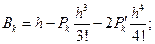
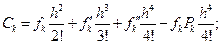
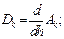
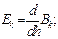
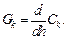
Здесь коэффициенты A, B, C, D, E, G известны, и их значения будут использованы ниже при решении конкретных задач. Будут использованы также формулы (12) как рекуррентные формулы при нахождении решения краевой задачи. Они представляют собой систему линейных алгебраических уравнений в виде четырехдиагональной матрицы.
Решать уравнения (12) можно методом Гаусса, последовательно исключая неизвестные переменные. В первой паре уравнений (12) известным будет 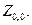 Следовательно, значения
Следовательно, значения 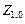 и
и  можно будет выразить через
можно будет выразить через 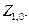 Этот процесс исключения можно продолжить для второй и последующих пар и всякий раз выражать
Этот процесс исключения можно продолжить для второй и последующих пар и всякий раз выражать  через
через 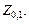 Предположим, что нам удалось сделать это для (k – 1)-й пары уравнений:
Предположим, что нам удалось сделать это для (k – 1)-й пары уравнений:
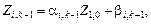
 (13)
(13)
Тогда, подставляя (13) в (12), получаем: 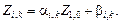 Сравнивая результат подстановки с последним выражением, получим рекуррентные формулы вычисления коэффициентов
Сравнивая результат подстановки с последним выражением, получим рекуррентные формулы вычисления коэффициентов 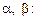
 (13а)
(13а)
Приведемпример решения уравнения 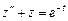 с граничными условиями
с граничными условиями 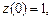
 Точное решение этого уравнения:
Точное решение этого уравнения:
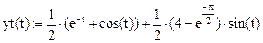

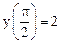
Дано: 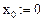


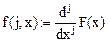
Зададим дискрет по x: 

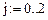
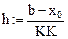
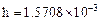
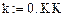
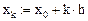
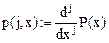
Краевые условия: 
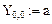

Получим дискретные значения функций 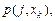
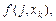 вычисленные в 3(KK + 1) точках.
вычисленные в 3(KK + 1) точках.
Введем дискретные значения коэффициентов, вычисленные в (KK + 1) точках:
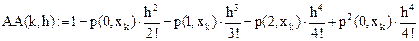
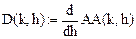
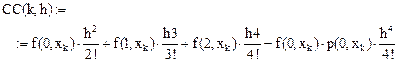
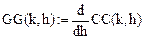
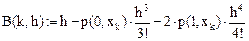

Обозначим (для единообразия): 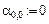


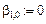 (таким образом, что
(таким образом, что 
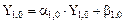 ) и вычислим:
) и вычислим:


Для визуальной проверки выведем на дисплей значения:
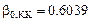
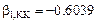

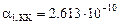
Заметим, что коэффициенты 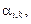
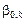 в данном примере не зависят от краевых (граничных) условий. Коэффициент
в данном примере не зависят от краевых (граничных) условий. Коэффициент  зависит от
зависит от  таким образом: при
таким образом: при 
 при
при 
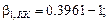 при
при 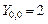
 и т. д.
и т. д.
Напомним граничные условия: 
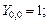
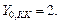
Исходя из (13), если задано 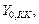 вычисляем:
вычисляем: 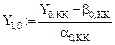
Если же задано  то получаем:
то получаем: 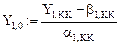
Вычислим далее: 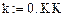
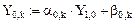
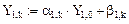
Выведем на дисплей значение: 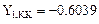
Остальные компоненты представлены в виде разворачиваемой в электронной версии пособия матрицы Y:
| |||||||||
| 1.0022 | 1.0044 | 1.0066 | 1.0088 | 1.011 | 1.0132 | ||||
| 1.3961 | 1.3961 | 1.396 | 1.396 | 1.396 | 1.396 | 1.396 |
Полученные приближенное и точное решения можно сравнить на графике (рис. 18).

Рис. 18
Задание.Привести пример других краевых условий, когда частного решения нет (в качестве примера можно взять граничные условия 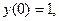
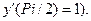
 |
3. Решение задач диффузии
методом конечных разностей
Постановка задачи
Рассмотрим стационарную задачу о нахождении распределения плотности потока нейтронов в одномерном реакторе, все характеристики которого зависят лишь от одной пространственной переменной х, т. е. задачу об определении одномерного нейтронного поля [1].
Пусть среда реактора занимает слой 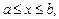 где a, b — границы слоя. Будем считать, что плотность потока нейтронов зависит только от параметра х и удовлетворяет стационарному уравнению диффузии, представляющему собой частный случай уравнения Больцмана:
где a, b — границы слоя. Будем считать, что плотность потока нейтронов зависит только от параметра х и удовлетворяет стационарному уравнению диффузии, представляющему собой частный случай уравнения Больцмана:
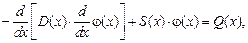
или
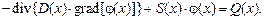
Здесь  — скорость изменения плотности потока нейтронов, или утечка нейтронов, 1/(см3×с);
— скорость изменения плотности потока нейтронов, или утечка нейтронов, 1/(см3×с); 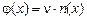 плотность потока нейтронов (1012...1013 1/см2× с); n — средняя скорость движения нейтронов, см/с;
плотность потока нейтронов (1012...1013 1/см2× с); n — средняя скорость движения нейтронов, см/с;  — плотность нейтронов, 1/см3;
— плотность нейтронов, 1/см3; 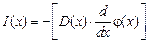 — плотность тока нейтронов, 1/(см2×с);
— плотность тока нейтронов, 1/(см2×с); 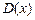 — коэффициент диффузии нейтронов (0,1...5 см);
— коэффициент диффузии нейтронов (0,1...5 см);  — макроскопическое сечение поглощения нейтронов ядрами среды (10–2...10–1 см–1); s — эффективное микроскопическое сечение поглощения нейтронов, см–2;
— макроскопическое сечение поглощения нейтронов ядрами среды (10–2...10–1 см–1); s — эффективное микроскопическое сечение поглощения нейтронов, см–2; 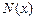 — ядерная плотность среды, см–3;
— ядерная плотность среды, см–3;  — скорость убыли нейтронов за счет поглощения (1010...1012 см–3×с–1);
— скорость убыли нейтронов за счет поглощения (1010...1012 см–3×с–1); 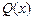 — скорость возрастания плотности нейтронов от внешних источников.
— скорость возрастания плотности нейтронов от внешних источников.
Поставленная задача решается с краевыми условиями третьего рода, которые записываются так:
 при
при 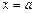 (аналогично при
(аналогично при  ).
).
Функции 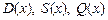 считаются кусочно-постоянными.
считаются кусочно-постоянными.
Для нахождения решения записанное выше уравнение Больцмана преобразуем к конечно-разностному виду (подробнее см. [1]):
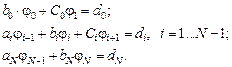
Эту систему конечно-разностных уравнений можно записать в векторно-матричной форме
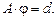 (14)
(14)
3.2. Алгоритм решения задачи в одной из систем
компьютерной математики
Матрица А размером 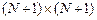 с элементами
с элементами 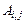 — трехдиагональная, симметричная (
— трехдиагональная, симметричная ( 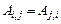 ) является квадратичной формой. Элементы
) является квадратичной формой. Элементы 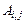 удовлетворяют условиям
удовлетворяют условиям  при
при 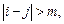 где
где  Матрицы такого типа называются
Матрицы такого типа называются 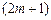 -диагональными. Матрица сильно разреженная. Решение уравнения (14) следует проводить методом прогонки (j, d —
-диагональными. Матрица сильно разреженная. Решение уравнения (14) следует проводить методом прогонки (j, d — 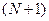 -компонентные векторы) [4].
-компонентные векторы) [4].
Условия зачетной лабораторной работы по коэффициенту диффузии  записаны в матрицу М повариантно:
записаны в матрицу М повариантно:
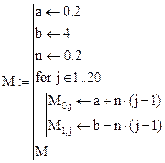
Дано: N — количество точек отсчета ( 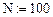 ); m — количество зон в реакторе (
); m — количество зон в реакторе ( 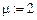 ); h — дискрет по переменной x
); h — дискрет по переменной x 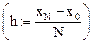 ; L — вектор координат зон реактора; VD — вектор, задающий коэффициент диффузии;
; L — вектор координат зон реактора; VD — вектор, задающий коэффициент диффузии; 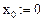

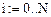
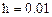
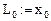
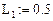
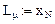
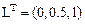
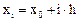
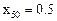


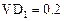
Номер столбца матрицы М является одновременно номером варианта.
Коэффициент диффузии 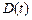 выразим через функцию Хевисайда
выразим через функцию Хевисайда 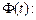
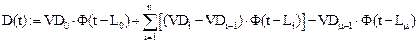
Дадим графическую интерпретацию коэффициента диффузии (рис. 19) и функции Хевисайда (рис. 20).
Переопределим индекс i: 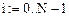
Запишем эффективное значение коэффициента диффузии на отрезке 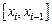 :
: 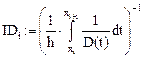
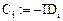
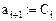
Зададим в каждой зоне вектор скорости возрастания плотности нейтронов от внешних источников 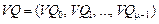 :
:
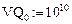
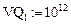

и вектор макроскопических сечений поглощения нейтронов ядрами среды 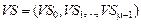 :
:
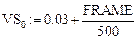

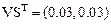
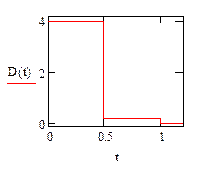
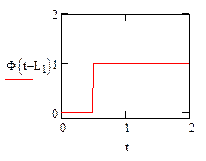
Рис. 19 Рис. 20
Используя функцию Хевисайда, зададим:

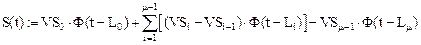
Построим графики этих функций (рис. 21, 22) и определим их средние значения на отрезке 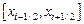 :
: 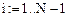
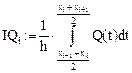

Введем обозначения: 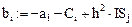
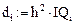
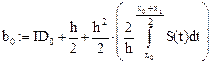
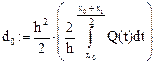
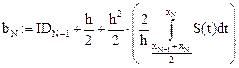
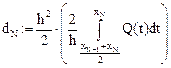
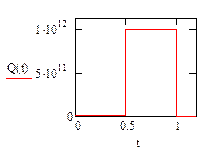

Рис. 21 Рис. 22
Рассмотрим алгоритм решения задачи методом прогонки.
Численное решение представлено вектором 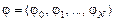 и отыскивается из уравнения
и отыскивается из уравнения 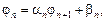

Рекуррентные формулы вычисления коэффициентов при прямом ходе: 


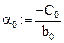
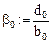
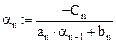

Вычисляя таким образом коэффициенты a и b, дойдем до шага 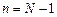 и получим уравнение
и получим уравнение
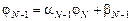 . (15)
. (15)
Но у нас есть еще последнее уравнение, связывающее 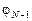 и
и  :
:
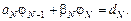 (16)
(16)
Решая уравнения (15) и (16) совместно, найдем
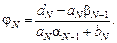
Другой вариант: при 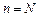 имеем
имеем 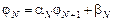 . В этом выражении должно быть:
. В этом выражении должно быть: 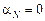 и
и  но
но 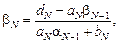 что и требовалось доказать. Таким образом:
что и требовалось доказать. Таким образом:

Получаем первый результат (компонента вектора решений): 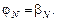 Затем при обратном ходе
Затем при обратном ходе 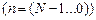 вычисляем все остальные компоненты вектора решений:
вычисляем все остальные компоненты вектора решений:
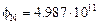
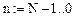
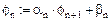
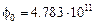
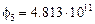

Возможна анимация (по параметру VS): в 35 кадрах записан диапазон изменения коэффициента диффузии 0,03…0,10.
Это позволяет в электронной версии методических указаний получить решение 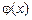 уравнения диффузии в виде клипа, отснятого по параметру VS (рис. 23).
уравнения диффузии в виде клипа, отснятого по параметру VS (рис. 23).
Результаты решения представлены ниже:
| ||||||||
| 4.783·1011 | 4.789·1011 | 4.795·1011 | 4.801 1011 | 4.807·1011 | 4.813·1011 |
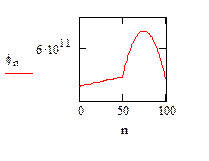
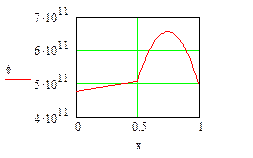
Рис. 23
3.3. Векторно-матричная запись уравнения диффузии
и его решение
Запишем алгоритм формирования матрицы A:

В программе все элементы матрицы формируются согласно условиям задания. Если таковые отсутствуют, то элементам матрицы по умолчанию присваиваются нули.
Зададим параметры:
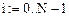

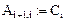

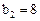
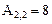
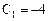

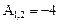
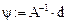
Получим решение:
| ||||||||
| 4.783·1011 | 4.789·1011 | 4.795·1011 | 4.801 1011 | 4.807·1011 | 4.813·1011 |
 Сравнив решения
Сравнив решения 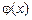 и
и  видим полное совпадение результатов. Время на их получение методом прогонки и при непосредственном решении векторно-матричного уравнения приблизительно одинаковое, если используются достаточно мощные персональные компьютеры. Это же можно сказать и о точности получаемых решений для данной задачи, имеющей сравнительно небольшой объем исходной информации, определяемой в основном матрицей А. Однако при увеличении размерности матрицы А временные затраты на получение решения методом прогонки значительно меньше, чем при решении векторно-матричного уравнения. Число арифметических операций, необходимых для получения решения в последнем случае (их число равно
видим полное совпадение результатов. Время на их получение методом прогонки и при непосредственном решении векторно-матричного уравнения приблизительно одинаковое, если используются достаточно мощные персональные компьютеры. Это же можно сказать и о точности получаемых решений для данной задачи, имеющей сравнительно небольшой объем исходной информации, определяемой в основном матрицей А. Однако при увеличении размерности матрицы А временные затраты на получение решения методом прогонки значительно меньше, чем при решении векторно-матричного уравнения. Число арифметических операций, необходимых для получения решения в последнем случае (их число равно 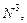 где
где 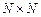 — размерность матрицы А) намного превосходит их число при решении методом прогонки. Это приводит к увеличению времени счета.
— размерность матрицы А) намного превосходит их число при решении методом прогонки. Это приводит к увеличению времени счета.
 |
Список литературы
1. Богомолов Г.И., Красников П.В. Метод конечных разностей в решении задач диффузии: Метод. указания к лаб. работе по курсу «Спецглавы высшей математики». М.: Изд-во МГТУ им. Н.Э. Баумана, 2001.
2. Бахвалов Н.С. Численные методы. М.: Наука, 1975.
3. Титов К.В. Решение одного класса нелинейных дифференциальных уравнений // Современные естественно-научные и гуманитарные проблемы: Сб. тр. М.: Логос, 2005.
4. Титов К.В. Решение задач математической физики в среде MathCAD. М.: Изд-во МГТУ им. Н.Э. Баумана, 2006.
Дата добавления: 2021-02-19; просмотров: 331;










