Метод стрельбы (пристрелки)

Рассмотрим особенности применения этого метода на примере решения уравнения 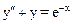с граничными условиями: 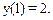Точное решение этого уравнения:

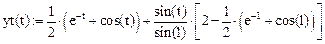
Проверим его граничные значения: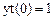

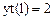
Заметим, что при граничных условиях: 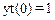данное уравнение решения не имеет.

Приведем алгоритм решения этого уравнения по методу стрельбы.

Дано: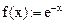

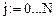
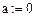
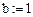
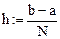
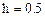
Перейдем к дискретным переменным: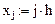

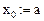
Левое граничное условие: если 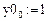, то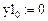

Здесь и далее введены обозначения: 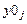— дискретные значения частного решения неоднородного дифференциального уравнения; 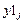— дискретные значения общего решения однородного дифференциального уравнения.

Произвольно задаем: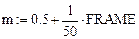

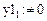
Этих данных достаточно, чтобы определить все остальные значения: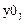

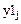
Алгоритм:

Запишем рекуррентные формулы вычисления частного и общего решений соответствующего неоднородного и однородного дифференциальных уравнений, представленных в разностном виде:

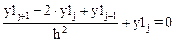
Выразим из этих уравнений:

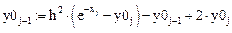
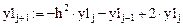
В конце вычислений находим:

Теперь выпишем все значения компонент вектора y: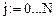

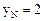
Сравнение полученных решений представлено на рис. 12 (возможна анимация графика только по параметру h, 100 кадров).

Рис. 12

Изменим в этой задаче граничные условияна 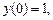и соответственно внесем коррективы в исходные данные: где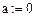

Число точек отсчета: 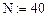; дискрет по х: 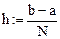, где 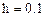. Выберем параметр анимации , знак (+, –): 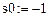, . Зададим дискретные начальные значения частного решения соответственно неоднородного и однородного исходного уравнения: , .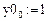

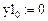Произвольно (как предлагается в [2, с. 549]) задаем: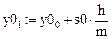

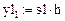
В режиме анимации проанализируем это утверждение.

Дискретные значения независимой переменной:

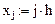
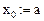
Запишем в разностном виде исходное неоднородное и однородное дифференциальные уравнения и их приближенные решения в дискретных точках:

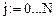
Получим:

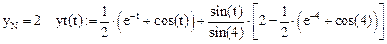
Проверим граничные условия: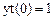

Анимация графика (рис. 13, по параметру h, 40 кадров) подтверждает приведенное в [2, с. 549] высказывание о произвольности выбора 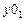и Рис. 14 иллюстрирует возможность задания вторичной оси (возможна анимация графика по параметру h,
40 кадров).

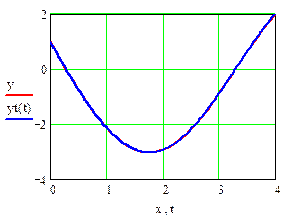
Рис. 13

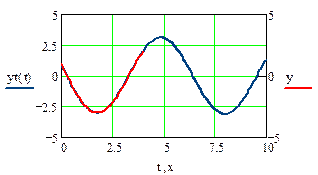
Рис. 14

При граничных условиях 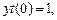данное уравнение решения не имеет. В этом случае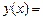
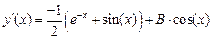и ,

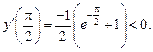
Упражнение 2.1

Решить численно методом стрельбы дифференциальное уравнение 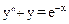с граничными условиями 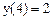. Заменить граничные условия другими и получить решение. Сравнить его с точным решением, построить график, снять анимационный клип.

Решение. Точное решение этого уравнения:

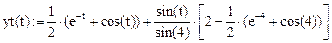
Оно удовлетворяет граничным условиям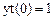

Приведем алгоритм решения этого уравнения по методу стрельбы.

Дано: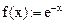

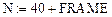
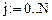
Перейдем к дискретным переменным: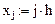

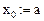
Граничные условия: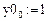

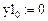
Здесь и далее введены обозначения: 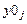— дискретные значения частного решения неоднородного дифференциального уравнения; 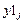— дискретные значения общего решения однородного дифференциального уравнения.

Произвольно задаем: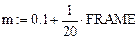

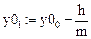
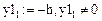
Алгоритм: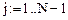

Запишем рекуррентные формулы вычисления частного и общего решений соответствующего неоднородного и однородного дифференциальных уравнений, представленных в разностном виде:

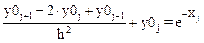
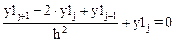
Выразим из этих уравнений:

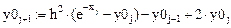
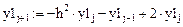
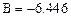
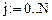
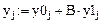
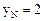
Решение дифференциального уравнения представлено на рис. 15 (возможна анимация графика только по параметру h, 100 кадров).

Рис. 15

Произвольно задаем: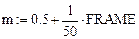

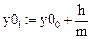
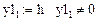
Зададим параметры, необходимые для построения графика
(рис. 16).

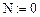
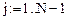
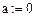
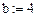
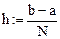
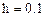
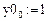
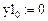
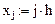
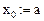
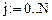
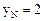
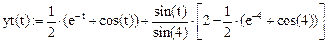
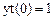
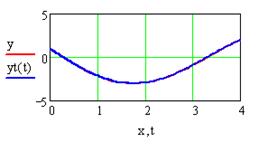
Рис. 16

Полученный график (см. рис. 16, возможна анимация графика,
100 кадров) не отличается от точного решения!

Упражнение 2.2

Решить численно методом стрельбы дифференциальное уравнение 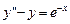с граничными условиями: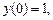 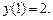Сравнить его решение с точным, построить график, снять анимационный клип.

Метод прогонки

Это один из вариантов метода Гаусса решения системы линейных алгебраических уравнений с сильно разреженной матрицей
[2, с. 552], имеющей вид:

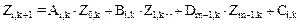
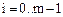
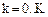
Здесь m — порядок дифференциального уравнения; K — число дискретных точек отсчета; i — порядок производной; 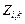— дискретные значения искомого решения, записываемые в матрицу Z.

Иллюстрацию этого метода проведем на решении уравнения: 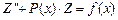с граничными условиями:

Перейдем к дискретным переменным: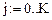

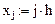
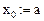
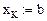
Запишем рекуррентные формулы вычисления решения исходного дифференциального уравнения, представленного в разностном виде:

Найдем из этого уравнения

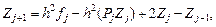
или

(4)

Обозначим: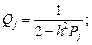

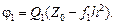
Изменяя 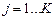и выражая всякий ра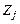з через дойдем, наконец, до уравнения

(5)

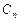где и 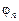— известные коэффициенты.

Подставим (5) в 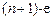уравнение (4). Вновь разрешая его, получим

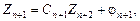
где 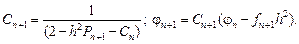(6)

Таким образом, коэффициенты уравнений (5), связывающих последующие значения 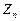и 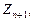можно определять из рекуррентных соотношений (6) при начальных условиях: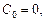 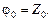Так как 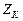известно, после нахождения всех коэффициентов можно последовательно определять 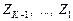из (5). Процесс вычисления коэффициентов принято называть прямым ходом прогонки, а процесс вычисления 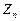— обратным ходом прогонки.

Рассмотрим особенности метода прогонки на примере решения уравнения 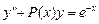с граничными условиями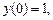 (следует заметить, что не для любых условий Неймана, Дирихле – Неймана краевые задачи имеют решение).

Найдем точное решение этого уравнения (при ):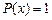

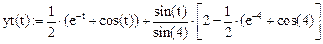
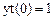
Введем обозначения: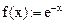

Дано: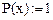

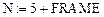
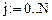
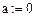
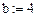
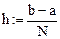
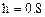
Перейдем к дискретным переменным: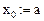

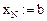
Граничные условия: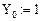

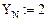
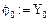
Здесь и далее введены обозначения: 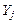— дискретные значения решения дифференциального уравнения; 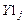— дискретные значения первой производной решения дифференциального уравнения. Согласно формулам (5) и (6), будем иметь:

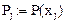
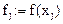
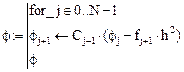
После нахождения всех коэффициентов можно последовательно определять 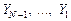таким образом: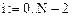 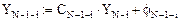. Решение представляется графически (рис. 17, возможна анимация графика по параметру h, 50 кадров).

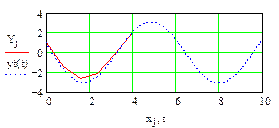
Рис. 17

Задание.Решить численно дифференциальное уравнение (4) для различных функций P(x): 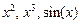и др., а также функций и др.