Метод Рунге – Кутта

Численное решение обыкновенных дифференциальных уравнений

Постановка задачи

Пусть дано дифференциальное уравнение первого порядка:

. (1)

Основная задача, связанная с этим уравнением, известна как задача Коши: найти решение уравнения (1) в виде функции у(х),удовлетворяющей начальному условию

(2)

Геометрически это означает, что требуется найти ин­тегральную кривую у = у(х), проходящую через заданную точку M₀ (x₀, у₀), при выполнении равенства (1). Существование и единственность решения задачи Коши для уравнения (1) обеспечиваются следующей теоремой.

Теорема Пикара. Если функция f(x, у) определена и непрерывна в некоторой плоской области G, определяемой неравенствами ׀х-х₀׀ ≤ а, ׀y-y₀׀ ≤ b, и удовлетворяет в этой области условию Липшица по у: суще­ствует такое положительное число М, что для любых точек (х; у₁) G и (х; у₂) G: |f(x,y₁) - f(x,y₂)| ≤ M·|y₁-y₂|, то на некотором отрезке |х - х₀| ≤ h существует, и притом толь­ко одно, решение у = у(х) урав­нения (1), удовлетворяющее начальному условию у₀= у(x₀).

Число М называется константой Липшица.

Если f(х, у) имеет ограниченную в G производную по у, то . Ве­личина h вычисляется по формул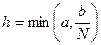е , где .

Существует несколько классов дифференциальных уравнений первого порядка, для которых решение может быть найдено аналитически (уравнения с разделяющимися переменными, одно­родные, линейные, в полных дифференциалах). Даже для таких уравнений решение не всегда удается довести до вида у = у(х), где у(x) — функция, с которой удобно работать дальше. Многие же дифференциальные уравнения, к которым приводят математичес­кие модели реальных процессов, не относятся к указанным клас­сам и аналитически решены быть не могут. Тем более это утверж­дение справедливо для систем дифференциальных уравнений и для уравнений старших порядков. По этой причине разработаны многочисленные методы приближенного решения дифференци­альных уравнений. В зависимости от формы пред­ставления решения, эти методы подразделяются на три основные группы:

- аналитические методы, применение которых дает приближен­ное решение дифференциального уравнения в виде формулы;

- графические методы, дающие приближенное решение в виде графика;

- численные методы, когда искомая функция получается в виде таблицы.

Метод Эйлера

В основе метода ломаных Эйлера лежит идея графического по­строения решения дифференциального уравнения, однако этот метод дает одновременно и способ нахождения искомой функции в численной (табличной) форме.

Пусть дано уравнение (1) с начальным условием (2) (т.е. поставлена задача Коши). Вначале найдем простейшим способом приближенное значение решения в некоторой точке х₁ = x₀ + h, где h достаточно малый шаг. Уравнение (1) совме­стно с начальным условием (2) задают направление касатель­ной к искомой интегральной кривой в точке М₀(х₀,y₀). Двигаясь вдоль этой касательной, получим приближенное значе­ние решения в точке х_1:

y₁ = y₀ + hf (x₀, y₀). (3)

Располагая приближенным решением в точке М₁(х_1, у₁), можно повторить описанную выше процедуру: построить прямую, проходящую через эту точку под углом, определяе­мым условием tgβ = f(x₁, y₁), и по ней найти приближен­ное значение решения в точке х₂ = x₁ + h. Эта прямая не есть касательная к реальной ин­тегральной кривой, поскольку точка М₁ нам недоступна. Одна­ко если h достаточно мало, то получаемые приближения будут близки к точным значениям решения.

Продолжая этот процесс, построим систему равноотстоящих точек x_i = х₀ + ih, где (i = 0,1,2,..., n). Получение таблицы значений иско­мой функции у(х) по методу Эйлера заключается в циклическом применении пары формул:

(4)

,

Геометрическая иллюстрация метода Эйлера приведена на рисунке. Вместо интегральной кривой в реальности получается со­вокупность прямых (так называемая ломаная Эйлера).

Методы численного интегрирования дифференциальных урав­нений, в которых решение получается от одного узла к другому, называются пошаговыми. Метод Эйлера — простейший представи­тель семейства пошаговых методов.

Оценка погрешности метода при таком элемен­тарном рассмотрении невозможна даже на первом шаге. Кроме того, особенностью любого пошагового метода является то, что, начиная со второго шага, исходное значение у_i в формуле (4) само является приближенным, т.е. погрешность на каждом следующем шаге систематически возрастает.

Наиболее используемым эмпирическим методом оценки точ­ности как метода Эйлера, так и других пошаговых методов при­ближенного численного интегрирования обыкновенных диффе­ренциальных уравнений является способ двойного прохождения заданного отрезка — с шагом h и с шагом h/2. Совпадение соот­ветствующих десятичных знаков в полученных двумя способами результатах дает эмпирические основание считать их верными (хотя полной уверенности в этом быть не может).

Метод Рунге – Кутта

Основная идея этого метода такова: вместо использования в рабочих формулах частных производных функции f(х, у) использовать лишь саму эту функцию, но на каж­дом шаге вычислять ее значения в нескольких точках.

Проиллюстрируем это на примере одного из возможных мето­дов второго порядка. Для метода Эйлера путем простейшей право­сторонней аппроксимации производной имеем: .

В это выражение входят значения функции в двух точках. Если взять в правой части уравнения (1) значение f(х, у) в точке с номером i, то придем к методу Эйлера. Однако можно рассудить и иначе: раз для аппроксимации производной взяты две точки, то лучшей аппроксимацией правой части уравнения будет полу­сумма . Тогда для нахождения у_i+1 получим равенство . Поскольку оно представляет собой уравнение для у_i+1, то решать его можно ме­тодом итераций, причем в качестве первого приближения взять то значение y_i+l, которое определяется методом Эйлера. В итоге получим расчетные формулы нового метода, обеспечивающего пошаго­вое интегрирование дифференциального уравнения (1).

(5)

где (6)

Формула (5) - лишь одна из множества возможных формул Рунге - Кутта 2-го порядка. Разные формулы Рунге - Кутта одного и того же порядка будут давать при использовании различные числовые зна­чения, но все они одного порядка точности. Чем выше порядок формул Рунге - Кутта, тем более точные значения они дают. На практике соблюдается некоторый компро­мисс между высоким порядком формул и их громоздкостью, с одной стороны, и объемом вычислений по ним для достижения заданной точности, с другой. Ниже приведена одна из самых по­пулярных формул 4-го порядка, часто называемая просто, без уточнений, формулой Рунге - Кутта:

(7)

где

(8)

причем вначале последовательно вычисляются r₁, r₂, r₃, r₄, а лишь затем y_i+1 - по формуле (7).

Общий недостаток методов Рунге-Кутта — отсутствие про­стых способов оценки погрешности метода. Погрешность на од­ном шаге оценить сравнительно нетрудно, гораздо труднее оце­нить накопление погрешностей на протяжении многих шагов. Широко используемый на практике для этих методов полуэмпи­рический способ контроля точности — двойной счет. Допус­тим, что — точное решение уравнения при х = х₀ + nh. Тог­да для рассмотренного выше метода 4-го порядка , где верхний индекс означает шаг, с которым вычислено при­ближенное значение. Точно так же при решении с шагом :

.

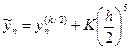Отсюда получаем: .

Следовательно, ошибка при вычислении с шагом есть

(9)

Из формулы (9), в частности, следует, что при достаточно малом h и малых погрешностях вычислений решение уравне­ния (1), полученное методом Рунге-Кутта 4-го порядка по фор­мулам (7) – (8), будет близким к точному.