Яблонский А.А. Курс теоретической механики. Ч 2, «Высшая школа», С-Птб.: 2002 и предшествующие издания.
Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. Ч.1 и 2. М., 1961 и последующие издания
Контрольные задания для СРС – ответить на следующие вопросы: 1). Влияют ли внутренние силы системы на ее количество движения? На движение ее центра масс? 2). При каких условиях центр масс системы находится в покое?
Лекция 15. Теорема об изменении кинетического момента.
Цель лекции - изложить теорему об изменении кинетического момента.
План лекции
1. Момент количества движения материальной точки и механической системы. Кинетический момент вращающегося тела
2. Теорема об изменении кинетического момента.
КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ
Для характеристики движения материальной точки используют еще одну векторную меру движения – момент количества движения, или кинетический момент, относительно центра.
Моментом количества движения материальной точки массой m относительно центра О называют векторную величину, равную векторному произведению радиус-вектора материальной точки, проведенного из этого центра, на количество движения точки:
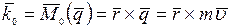
Единица измерения в системе СИ – 1 кг ∙ м2/с.
Главным моментом количества движения, или кинетическим моментом механической системы относительно центра О называют геометрическую сумму векторов моментов количеств движения материальных точек системы относительно этого же центра:
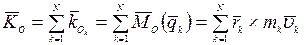
Пусть твердое тело вращается вокруг неподвижной оси Oz с угловой скоростью 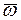 .Определим кинетический момент вращающегося тела относительно оси Oz. Согласно определению,
.Определим кинетический момент вращающегося тела относительно оси Oz. Согласно определению,
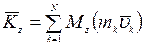 .
.
Проекции скорости точки Ак тела на касательную к траектории движения 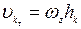 , а момент количества движения точки относительно оси Oz
, а момент количества движения точки относительно оси Oz
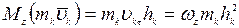 ,
,
где 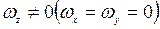 .
.
Подставив 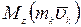 , получим:
, получим: 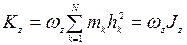 .
.
Здесь 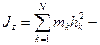 момент инерции тела относительно оси вращения.
момент инерции тела относительно оси вращения.
Окончательно имеем: 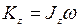 . Знак
. Знак 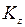 определяется знаком проекции угловой скорости
определяется знаком проекции угловой скорости 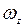 . Формула
. Формула
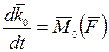
выражает теорему об изменении момента количества движения (кинетического момента) материальной точки: первая производная по времени от момента количества движения точки относительно центра О равна моменту равнодействующей силы относительно этого же центра О.
Для механической системы, состоящей из 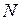 материальных точек, к каждой из которой приложены равнодействующие внешних
материальных точек, к каждой из которой приложены равнодействующие внешних 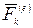 и внутренних сил
и внутренних сил 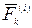 , запишем теорему об изменении кинетического момента относительно неподвижного центра О:
, запишем теорему об изменении кинетического момента относительно неподвижного центра О:
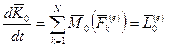 ,
,
где 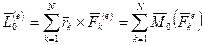 - главный момент внешних сил,
- главный момент внешних сил,
а главный момент внутренних сил 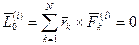 .
.
Последняя формула выражает теорему об изменении главного момента количеств движения (кинетического момента) механической системы: первая производная от главного момента количеств движения механической системы относительно неподвижного центра О равен главному моменту внешних сил, приложенных к точкам системы, относительно этого же центра.
Теорема допускает первый интеграл (закон сохранения кинетического момента), если
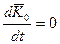 .
.
После интегрирования получим: 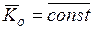 . Это уравнение выражает закон сохранения кинетического момента относительно центра О.
. Это уравнение выражает закон сохранения кинетического момента относительно центра О.
Рекомендуемая литература
Дата добавления: 2016-07-22; просмотров: 2086;










