Определение погрешностей обработки методом математической статистики
Лекция 7. Методы исследования и регулирования точности
7.1 Случайные погрешности обработки.
7.2 Методы исследования и регулирования точности.
Определение погрешностей обработки методом математической статистики
В основу метода положены приемы математической статистики для обработки данных, полученных при измерении контролируемого размера всей партии обработанных деталей. Для построения эмпирических кривых распределения погрешностей необходимо знать промежуток, в котором заключены размеры изучаемой партии деталей. Этот промежуток разбивается на равные по величине интервалы, после чего определяется частость  повторения отклонений размеров в партии
повторения отклонений размеров в партии

где 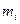 – число деталей, фактические отклонения размеров которых находятся в пределах каждого интервала;
– число деталей, фактические отклонения размеров которых находятся в пределах каждого интервала;
n – общее число деталей в партии.
На графике по оси абсцисс откладываются фактические размеры L детали, а по оси ординат – частость  их повторения. Полученные точки соединяются прямыми. Получается полигон распределения размеров. При увеличении числа деталей в партии и числа интервалов ломаная линия полигона приближается к плавной кривой.
их повторения. Полученные точки соединяются прямыми. Получается полигон распределения размеров. При увеличении числа деталей в партии и числа интервалов ломаная линия полигона приближается к плавной кривой.
Построение и изучение кривых распределения погрешностей позволяет отделить влияние, постоянных систематических погрешностей, от влияния погрешностей случайных, а также в ряде случаев доказать величину случайных погрешностей на основании обследования ранее обработанных партий деталей.
Из центральной предельной теоремы теории вероятностей следует, что при достаточно большом числе независимых случайных величин закон распределения их суммы близок к закону нормального распределения при условии, что ни одна из них не играет преобладающей роли по сравнению со всеми остальными.
Полигон и кривая распределения размеров партии деталей


Рис. 5.1. а) – полигон распределения фактических размеров; б) – теоретическая кривая распределения размеров
Кривые нормального распределения характеризуются двумя основными величинами: средним размером Lср и средним квадратичным отклонением  .
.
Средний размер равен:
 =
=  =
= 
где Li –размер отдельной детали, мм ;
n – число деталей в партии.
Среднее квадратичное отклонение равно:

где xi-отклонение размера этого среднего значения ,мм ;

Разность между наибольшими и наименьшими действительными размерами деталей в партии называют размахом распределения, или полем рассеивания

Кривая нормального распределения погрешностей выражается уравнением:

При проведении исследований, чтобы сопоставить графически определить, насколько полученная кривая рассеивания фактических размеров приближается к теоретической кривой нормального распределения, обе кривые вычерчиваются совмещенно, в одинаковом масштабе с этой целью рассчитывают данные, необходимые для построения кривой нормального распределения. Для сокращения расчетов можно ограничиться определением только трех параметров: максимальной ординаты ymax (при x = 0), ординаты для точек перегиба  (при
(при  ) и величиной поля рассеивания Dp. В целях приведения кривой нормального распределения к тому же масштабу, в котором вычерчена кривая распределения фактических размеров, необходимо ординаты, вычисленные по обычным формулам, умножить на величину интервала размеров (DL) и на величину, равную полному числу деталей в партии (n). С учетом этого обстоятельства расчётные формулы для построения кривой нормального распределения имеют следующий вид:
) и величиной поля рассеивания Dp. В целях приведения кривой нормального распределения к тому же масштабу, в котором вычерчена кривая распределения фактических размеров, необходимо ординаты, вычисленные по обычным формулам, умножить на величину интервала размеров (DL) и на величину, равную полному числу деталей в партии (n). С учетом этого обстоятельства расчётные формулы для построения кривой нормального распределения имеют следующий вид:

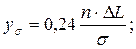
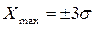
Для определения вероятности совпадения заданного допуска обработки в исследуемой операции на чертеже кривой теоретического распределения отмечаются границы допустимых значений размеров. Часть площади кривой распределения, ограниченная предельными раз-ми, соответствует количеству деталей, размеры которых не выходят за пределы поля допуска. Вероятность получения деталей в пределах поля допуска равняется отношению площади, заключенной у кривой распределения и ординатами, проведенными через концы допуска, ко всей площади кривой распределения.
Для определения величины соответствующих площадей (ограниченными верхним и нижним пределом допуска), расположенных по обе стороны центра распределения, используется приведенная Функция Лапласа при аргументе  :
:
 .
.
Значения аргумента Z для верхнего ( Zb ) и ( Zн ) предельных значений допуска равно:
Zв= (Lв-Lср)/s ; Zн= (Lн-Lср)/s
Вероятность получения брака t (в %) по верхнему пределу допуска равна:

по нижнему пределу допуска:
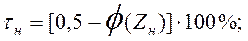
Полная вероятность выхода бракованных изделий равна:

Схема для определения вероятности брака:
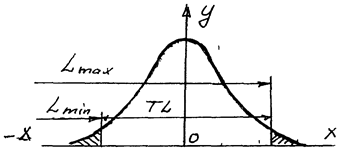
Рис. 5.2.
Дата добавления: 2016-07-05; просмотров: 2140;










