Энергетические уровни вблизи одной из брэгговских плоскостей

Простейшим и наиболее важным примером предыдущего анализа является случай, когда два уровня свободных электронов расположены близко друг к другу (по сравнению с ), но далеко от остальных уровней (также по сравнению с ). Если это так, то уравнения (5.19) сводятся к двум уравнениям

, (5.20)

Поскольку речь идет о двух уровнях, то нет необходимости пользоваться симметричными обозначениями. Введем переменные, удобные для двухуровневой задачи

, (5.21)

и запишем (5.20) в виде

(5.22)

Справедливы следующие соотношения:

при (5.23)

Энергия равна 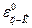для некоторого вектора обратной решетки, только в случае, если выполняется условие . Это означает (рис. 5.2, a), что точка лежит на брэгговской плоскости, которая перпендикулярна отрезку, соединяющему начальную точку в k-пространстве с точкой обратной решетки, и делит этот отрезок пополам.

Рис. 5.2, а рис. 5.2,б

С геометрической точки зрения условие (5.23) означает, что точка должна быть близка к одной брэгговской плоскости (но далека от места пересечения двух и более брэгговских плоскостей). Следовательно, случай двух почти вырожденных уровней относится к электрону, волновой вектор которого почти точно удовлетворяет условию однократного брэгговского рассеяния. Слабый периодический потенциал сильнее всего влияет на почти вырожденные уровни, поэтому главное воздействие слабый периодический потенциал оказывает лишь на те уровни свободного электрона, волновые векторы которых близки к векторам, допускающим брэгговское отражение.

Изучение структуры энергетических уровней, возникающих в слабом потенциале, начнем с рассмотрения случая, когда существенна лишь одна брэгговская плоскость и структура уровней определяется уравнениями (5.22). Эти уравнения имеют решение при выполнении условия

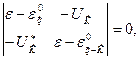(5.24)

из которого следует квадратное уравнение

. (5.25)

Его два корня

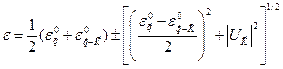(5.26)

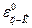Описывают главный результат воздействия периодического потенциала на два уровня и свободных электронов, когда точка близка к брэгговской плоскости, определяемой вектором . Эти решения показаны на рис. 5.3.

Выражение (5.26) приобретает особенно простой вид для точек, лежащих непосредственно на брэгговской плоскости, так как если принадлежит брэгговской плоскости, = 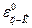. Следовательно,

, (5.27)

если лежит на одной брэгговской плоскости.

Таким образом, для всех точек на брэгговской плоскости один из уровней повышается на величину , а второй понижается на ту же постоянную величину.

Исходя из (5.26) можно также показать, что при = 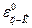выполняется соотношение

(5.28)

т.е. если точка лежит на брэгговской плоскости, то градиент параллелен этой плоскости (рис.5.2, б). Поскольку градиент перпендикулярен изоэнергетическим поверхностям, то эти поверхности перпендикулярны брэгговской плоскости.

Если точка принадлежит одной брэгговской плоскости, то можно также определить вид волновых функций, отвечающих двум решениям . Из (5.22) следует, что если дается выражением (5.27), то два коэффициента 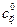и 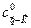удовлетворяют соотношению

. (5.29)

Поскольку два этих коэффициента доминируют в разложении (5.1) по плоским волнам, получим в первом приближении

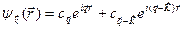. (5.30)

Условие двухкомпонентного представления волновой функции

. (5.31)

Это условие совпадает с известным правилом Вульфа-Брэгга для отражения электронов и рентгеновских лучей. Брэгговское отражение объясняет физический смысл двухкомпонентного приближения: в составлении волновой функции равноправно участвуют падающий и дифрагированный пучки.

При с учетом (5.30)

(5.32)

Это следует из того, что на брэгговской поверхности, где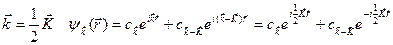

Если то

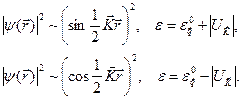(5.33)

Иногда два найденных типа линейных комбинаций называют волновыми функциями «s-типа» и «p-типа» , учитывая их зависимость от координат вблизи точек решетки. Комбинации s-типа, как и для атомных s-уровней, не обращаются в нуль на ионе; в комбинации р-типа плотность заряда для малых расстояний изменяется пропорционально квадрату расстояния от иона и обращается в нуль на ионе, что характерно для атомных р-уровней.