Общий подход к уравнению Шредингера в случае слабого потенциала

Когда периодический потенциал равен нулю, решения уравнения Шредингера представляют собой плоские волны. В случае слабого периодического потенциала волновую функцию блоховского уровня с квазиимпульсом можно записать в форме (4.39)

, (5.1)

где коэффициенты и энергия уровня определяются системой уравнений (4.38):

. (5.2)

Сумма в (5.1) берется по всем векторам обратной решетки; при фиксированном имеется по одному уравнению вида (5.2) для каждого вектора обратной решетки. Бесконечное множество различных решений уравнений (5.2) при заданном нумеруется значениями числа - номера зоны.

В случае свободных электронов все Фурье-компоненты равны нулю. Уравнение (5.2) примет вид

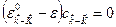, (5.3)

где введено обозначение

. (5.4)

Из уравнения (5.3) следует, что для любого должно выполняться условие = 0 или условие . Последнее может иметь место лишь для одного , кроме случаев, когда имеет одно и то же значение при нескольких различных значениях . Если такое вырождение отсутствует, то получаем обычные решения для свободных электронов:

, . (5.5)

Если, однако, имеется такая группа волновых векторов обратной решетки, для которых

, (5.6)

то при энергии , равной значению (5.6), существует независимых вырожденных решений вида плоской волны. Поскольку любая линейная комбинация вырожденных решений также является решением, остается полная свобода в выборе коэффициентов при .

Эти простые замечания приобретают более глубокое содержание, если значения не равны нулю, но очень малы. Будем по-прежнему проводить анализ для двух случаев, которые соответствуют наличию или отсутствию вырождения для электронов. Только теперь, проводя такое разделение, считаем, что энергия двух и более различных уровней свободных электронов равны друг другу с точностью до членов порядка .

Случай 1. Будем считать вектор фиксированным и рассмотрим такой вектор обратной решетки, для которого выполняется условие

для заданного и всех , (5.7)

т.е. энергия свободного электрона при отличается от его значения при всех других на величину, значительно превышающую (рис. 5.1). Будем рассматривать воздействие потенциала на такой уровень свободного электрона, для которого

(5.8)

Полагая в уравнениях (5.2) и используя обозначение (5.4), находим (штрих у индекса суммирования опускаем)

. (5.9)

Поскольку мы выбрали аддитивную постоянную в потенциальной энергии таким образом, чтобы при = 0, в правой части уравнения (5.9) имеются только члены с . Так как мы рассматриваем решение, для которого обращается в нуль при в пределе → 0, следует ожидать, что члены в правой части уравнения (5.9) будут иметь второй порядок малости по . Это можно проверить непосредственно, записав уравнение (5.2) для в виде

. (5.10)

Мы выделили из суммы (5.10) слагаемое, которое содержит , так как по порядку величины оно превосходит все другие члены, включающие при . Это следует из предположения (5.7), согласно которому уровень не является почти вырожденным по отношению к другим уровням . В противном случае некоторые из знаменателей в (5.10) имели бы малую величину порядка ; в результате множитель в числителе сокращался бы и в сумме в (5.10) возникли бы дополнительные слагаемые, сравнимые по величине со слагаемым, содержащим .

Поэтому в отсутствие приближенного вырождения имеем

(5.11)

Подставляя это выражение в (5.9), находим

(5.12)

Следовательно, возмущенный уровень энергии отличается от значения для свободного электрона на величину порядка . Поэтому, чтобы решить уравнение (5.12) для с такой точностью, достаточно заменить справа в знаменателе на ; в результате получаем следующее выражение для с точностью до второго порядка по :

(5.13)

Уравнение (5.13) показывает, что слабо возмущенные невырожденные зоны отталкивают друг друга: каждый уровень , лежащий ниже , дает вклад в (5.13), повышающий величину , а каждый уровень, расположенный выше , дает вклад, понижающий эту энергию.

Однако наиболее важный качественный вывод, который следует из этого анализа, заключается в том, что сдвиг энергии по сравнению со значением для свободных электронов имеет второй порядок малости по энергии .

В дальнейшем будет показано, что при наличии приблизительного вырождения такой сдвиг энергии может быть линейным по . Следовательно, в слабом периодическом потенциале значительный сдвиг испытывают лишь почти вырожденные уровни свободных электронов. Этому важному случаю и нужно уделить главное внимание.

Случай 2. Пусть величина такова, что имеются векторы обратной решетки, для которых энергии отличаются друг от друга на величину порядка , тогда разность между этими энергиями и энергией велика по сравнению с ,

. (5.14)

В этом случае мы должны рассматривать отдельно те из уравнений системы (5.2), для которых есть одно из значений . Это дает уравнений, соответствующих уравнению (5.9) в невырожденном случае. В получаемых уравнениях выделяем из суммы те члены, которые содержат коэффициенты . Эти члены могут и не быть малыми в пределе стремящегося к нулю взаимодействия в отличие от других членов, которые имеют порядок выше . В результате получим

. (5.15)

Выделяя таким же образом члены в сумме, можно записать уравнение (5.2) для остальных уровней в виде

. (5.16)

Последнее уравнение соответствует уравнению (5.10) в случае отсутствия приблизительного вырождения.

Поскольку при коэффициенты имеют порядок выше , уравнения (5.16) дают

. (5.17)

Подставляя эти выражения в (5.15), получим

. (5.18)

Сравним полученные уравнения с результатом (5.12) для случая, когда приблизительное вырождение отсутствует. Там было получено явное выражение для сдвига энергии с точностью до (система уравнений (5.18) переходит в него при ). Теперь, однако, видно, что с точностью до определение сдвигов для почти вырожденных уровней сводится к решению системы из уравнений для . При этом коэффициенты во второй сумме справа в этих уравнениях имеют более высокий порядок по , чем в первой. Следовательно, чтобы найти основные поправки по величине , можно заменить (5.18) системой гораздо более простых уравнений: