Производная сложной функции
Определение 1. Функция 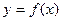 называется дифференцируемой в точке
называется дифференцируемой в точке 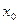 , если ее приращение в этой точке представимо в виде
, если ее приращение в этой точке представимо в виде
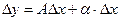 , (2.1)
, (2.1)
где 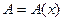 и не зависит от
и не зависит от 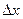 , а
, а 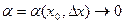 при
при 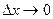 .
.
Теорема 1. Функция 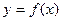 , дифференцируема в точке
, дифференцируема в точке 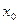 тогда и только тогда, когда она имеет в этой точке конечную производную
тогда и только тогда, когда она имеет в этой точке конечную производную 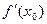 .
.
Доказательство. Необходимость. Пусть функция 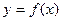 дифференцируема в точке
дифференцируема в точке 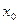 , т.е. имеет место равенство (2.1). Разделив его на
, т.е. имеет место равенство (2.1). Разделив его на 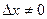 , получим
, получим 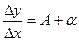 . Переходя к пределу при
. Переходя к пределу при 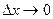 , видим, что
, видим, что 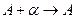 , т.е. предел правой части существует и равен А, значит, существует и предел левой части, т.е.
, т.е. предел правой части существует и равен А, значит, существует и предел левой части, т.е. 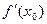 , причем
, причем 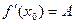 .
.
Достаточность. Пусть существует 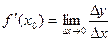 . Тогда по теореме 1 § 16 главы 1
. Тогда по теореме 1 § 16 главы 1 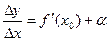 , где
, где 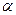 – бесконечно малая функция при
– бесконечно малая функция при 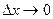 . Отсюда
. Отсюда 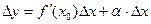 , т.е. функция дифференцируема в точке
, т.е. функция дифференцируема в точке 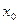 .
.
Теорема доказана.
Замечание. Из теоремы 1 следует, что понятия функции, имеющей конечную производную, и дифференцируемой функции равносильны. Поэтому дифференцируемой можно назвать функцию, имеющую конечную производную, что и делают авторы некоторых учебников.
Как связаны между собой свойства непрерывности и дифференцируемости функций? Имеет место
Теорема 2.Если функция 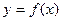 дифференцируема в точке
дифференцируема в точке 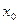 , то она в этой точке непрерывна.
, то она в этой точке непрерывна.
Доказательство. Поскольку в точке 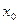
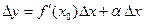 , имеем
, имеем 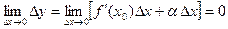 , что и означает непрерывность функции в точке
, что и означает непрерывность функции в точке 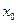 .
.
Теорема доказана.
Обратное неверно, то есть существуют непрерывные функции, которые не дифференцируемы.
Пример 1. Покажем, что функция 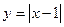 непрерывна, но не дифференцируема в точке
непрерывна, но не дифференцируема в точке 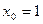 .
.
Решение. Найдем приращение функции в точке 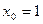 , соответствующее приращению
, соответствующее приращению 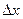 аргумента. Имеем
аргумента. Имеем 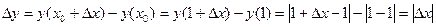 . Поэтому
. Поэтому 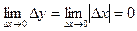 , то есть функция
, то есть функция 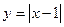 непрерывна в точке
непрерывна в точке 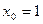 . С другой стороны,
. С другой стороны, 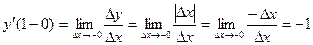 ,
, 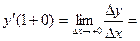
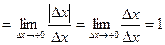 , то есть односторонние производные в точке
, то есть односторонние производные в точке 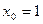 не равны, следовательно, данная функция в этой точке не дифференцируема.
не равны, следовательно, данная функция в этой точке не дифференцируема.
В математическом анализе имеются примеры функций, которые в каждой точке числовой прямой непрерывны, но не дифференцируемы. Они имеют сложную конструкцию.
Теорема 3. Пусть функция 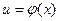 имеет в точке
имеет в точке 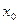 производную
производную 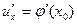 , функция
, функция 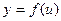 имеет в соответствующей точке
имеет в соответствующей точке 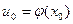 производную
производную 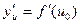 . Тогда сложная функция
. Тогда сложная функция 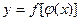 имеет в точке
имеет в точке 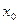 производную
производную
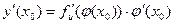 или, короче,
или, короче, 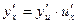 .
.
Доказательство. Дадим значению 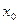 приращение
приращение 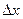 . Тогда получим соответствующее приращение
. Тогда получим соответствующее приращение 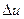 функции
функции 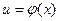 и приращение
и приращение 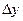 функции
функции 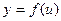 . В силу теоремы 1 имеем
. В силу теоремы 1 имеем
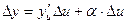 , где
, где 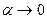 при
при 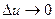 .
.
Отсюда
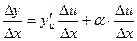 .
.
Заметим, что если 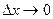 , то и
, то и 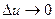 по теореме 2, поэтому и
по теореме 2, поэтому и 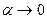 . Следовательно,
. Следовательно, 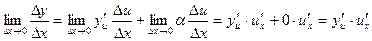 .
.
Поскольку существует предел правой части равенства, то существует и предел левой части и
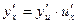 .
.
Теорема доказана.
Замечание. Теорема 3 доказана для случая, когда сложная функция 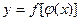 имеет одну промежуточную переменную
имеет одну промежуточную переменную 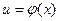 . Если промежуточных переменных несколько, то производная вычисляется аналогично. Например, если
. Если промежуточных переменных несколько, то производная вычисляется аналогично. Например, если 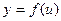 ,
, 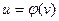 ,
, 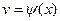 , то
, то 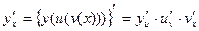 .
.
Дата добавления: 2016-06-09; просмотров: 1330;










