Абсолютная и относительная погрешности функции
При выполнении операций над приближенными числами можно записать оценки для вычисления функций, аргументами которых являются приближенные числа. Общее правило, основанное на вычислении приращения (погрешности) функций при заданных приращениях (погрешностях) аргументов, заключается в следующем:
Пусть в некоторой области 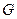
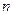 -мерного евклидова пространства задана непрерывно дифференцируемая функция
-мерного евклидова пространства задана непрерывно дифференцируемая функция 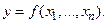 Как правило, в практических задачах известны лишь приближенные значения аргументов
Как правило, в практических задачах известны лишь приближенные значения аргументов 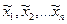 такие, что
такие, что 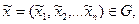 и их абсолютные и относительные погрешности. Вычислим приближенное значение функции по формуле
и их абсолютные и относительные погрешности. Вычислим приближенное значение функции по формуле 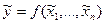 и оценим его абсолютную и относительную погрешности.
и оценим его абсолютную и относительную погрешности.
Если воспользоваться формулой Лагранжа, то, предполагая, что 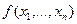 непрерывно дифференцируема и ее первые частные производные незначительно меняются в области
непрерывно дифференцируема и ее первые частные производные незначительно меняются в области 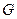 , получаем:
, получаем:
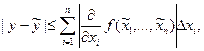
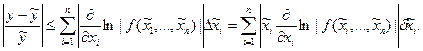
Поэтому, можно положить, что
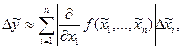 (1.1)
(1.1)
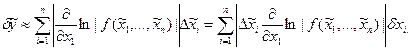 (1.2)
(1.2)
Формулы (1.1), (1.2) позволяют оценить абсолютную и относительную погрешности любого выражения, в том числе суммы, разности, отношения и т.д.
Нередко приходится сталкиваться с ситуацией, когда функция 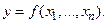 задается не явной формулой, а как решение нелинейного уравнения
задается не явной формулой, а как решение нелинейного уравнения 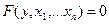 , т.е. неявно. Если для такой неявной функции воспользоваться известными формулами нахождения производных
, т.е. неявно. Если для такой неявной функции воспользоваться известными формулами нахождения производных 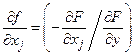 , вычисленными
, вычисленными 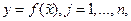 , то исследование погрешностей неявной функции сводится к рассмотренному выше случаю.
, то исследование погрешностей неявной функции сводится к рассмотренному выше случаю.
Определение 4. Задачу вычисления погрешностей функции в случае, когда заданы погрешности аргументов, называют прямой задачей теории погрешностей.
Часто приходится находить такие допустимые неизвестные погрешности аргументов, чтобы погрешность функции не превышала заданного 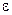 (эпсилон).
(эпсилон).
Определение 5. Задача определения допустимой погрешности аргументов по заданной допустимой погрешности функции называется обратной задачей теории погрешностей.
Для функции одной переменной 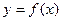 допустимую абсолютную погрешность аргумента, если
допустимую абсолютную погрешность аргумента, если 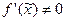 , можно приближенно вычислить по формуле
, можно приближенно вычислить по формуле
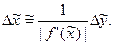
Для функции нескольких переменных 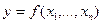 обратная задача теории погрешностей не имеет общего алгоритма решения, а решается только при ряде ограничений. Например, если значения всех аргументов можно одинаково легко определить с любой точностью, то применяют принцип равных влияний, т.е. считают, что все слагаемые в формуле (*) равны между собой. В этом случае допустимые абсолютные погрешности аргументов находят по формулам
обратная задача теории погрешностей не имеет общего алгоритма решения, а решается только при ряде ограничений. Например, если значения всех аргументов можно одинаково легко определить с любой точностью, то применяют принцип равных влияний, т.е. считают, что все слагаемые в формуле (*) равны между собой. В этом случае допустимые абсолютные погрешности аргументов находят по формулам
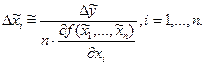
Если значение одного из аргументов значительно труднее измерить или вычислить с той же точностью, что и значения остальных аргументов, то погрешность именно этого аргумента надо согласовать с требуемой погрешностью функции.
Сформулируем правила оценки предельных погрешностей при выполнении операций над приближенными числами.
При сложении или вычитании чисел их абсолютные погрешности складываются. Относительная погрешность суммы заключена между наибольшим и наименьшим значениями относительных погрешностей слагаемых; на практике принимается наибольшее значение.
При умножении или делении чисел друг на друга их относительные погрешности складываются. При возведении в степень приближенного числа его относительная погрешность умножается на показатель степени.
Для случая двух приближенных чисел 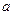 и
и 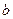 эти правила можно записать в виде формул:
эти правила можно записать в виде формул:
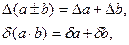
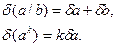
Пример 3. Найти относительную погрешность функции
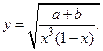
Используя формулы, получаем:
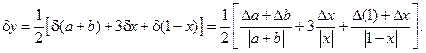
Полученная оценка относительной погрешности содержит в знаменателе выражение 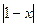 . Ясно, что при
. Ясно, что при 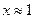 можем получить очень большую погрешность, в этом случае целесообразно раскрыть скобки в знаменателе исходной функции.
можем получить очень большую погрешность, в этом случае целесообразно раскрыть скобки в знаменателе исходной функции.
Ловушки вычислений
Полученная оценка относительной погрешности содержит в знаменателе выражение 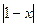 . Ясно, что при
. Ясно, что при 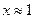 можем получить очень большую погрешность. В связи с этим рассмотрим подробнее случай вычитания близких чисел.
можем получить очень большую погрешность. В связи с этим рассмотрим подробнее случай вычитания близких чисел.
Запишем выражение для относительной погрешности разности двух чисел в виде
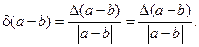
При 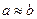 эта погрешность может быть сколь угодно большой.
эта погрешность может быть сколь угодно большой.
Пример 4. Пусть 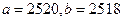 . В этом случае имеем абсолютные погрешности исходных данных
. В этом случае имеем абсолютные погрешности исходных данных 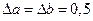 и относительные погрешности
и относительные погрешности 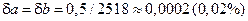 . Относительная погрешность разности равна
. Относительная погрешность разности равна
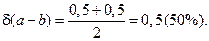
Следовательно, при малых погрешностях в исходных данных мы получили весьма неточный результат. Нетрудно подсчитать, что даже при случайных изменениях 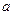 и
и 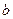 на единицу, в последних разрядах их разность может принимать значения 0, 1, 2, 3, 4. Поэтому, при организации вычислительных алгоритмов следует избегать вычитания близких чисел; при возможности алгоритм нужно видоизменить во избежание потери точности на некотором этапе вычислений.
на единицу, в последних разрядах их разность может принимать значения 0, 1, 2, 3, 4. Поэтому, при организации вычислительных алгоритмов следует избегать вычитания близких чисел; при возможности алгоритм нужно видоизменить во избежание потери точности на некотором этапе вычислений.
Из рассмотренных правил следует, что при сложении или вычитании приближенных чисел желательно, чтобы эти числа обладали одинаковыми абсолютными погрешностями, т. е. одинаковым числом разрядов после десятичной точки. Например, 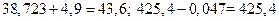 . Учет отброшенных разрядов не повысит точность результатов. При умножении и делении приближенных чисел количество значащих цифр выравнивается по наименьшему из них.
. Учет отброшенных разрядов не повысит точность результатов. При умножении и делении приближенных чисел количество значащих цифр выравнивается по наименьшему из них.
Рассмотрим также некоторые другие случаи, когда можно избежать потери точности правильной организацией вычислений.
Пусть требуется найти сумму пяти четырехразрядных чисел: 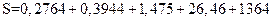 . Складывая все эти числа, а затем, округляя полученный результат до четырех значащих цифр, получаем
. Складывая все эти числа, а затем, округляя полученный результат до четырех значащих цифр, получаем 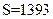 . Однако при вычислении на машине округление происходит после каждого сложения. Предполагая условно сетку четырехразрядной, проследим вычисление на машине суммы чисел от наименьшего к наибольшему, т. е. в порядке их записи: 0,2764+0,3944=0,6708, 0,6708+1,475=2,156, 2,156+26,46=28,62, 28,62+1364=393; получили
. Однако при вычислении на машине округление происходит после каждого сложения. Предполагая условно сетку четырехразрядной, проследим вычисление на машине суммы чисел от наименьшего к наибольшему, т. е. в порядке их записи: 0,2764+0,3944=0,6708, 0,6708+1,475=2,156, 2,156+26,46=28,62, 28,62+1364=393; получили 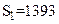 , т. е. верный результат. Изменим теперь порядок вычислений и начнем складывать числа последовательно от последнего к первому: 1364+26,46=1390, 1390+1,475=1391, 1391+0,3944=1391, 1391+0,2764=1391; здесь окончательный результат
, т. е. верный результат. Изменим теперь порядок вычислений и начнем складывать числа последовательно от последнего к первому: 1364+26,46=1390, 1390+1,475=1391, 1391+0,3944=1391, 1391+0,2764=1391; здесь окончательный результат 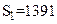 , он менее точный.
, он менее точный.
Анализ процесса вычислений показывает, что потеря точности здесь происходит из-за того, что прибавления к большому числу малых чисел не происходит, поскольку они выходят за рамки разрядной сетки ( 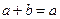 при
при 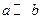 ). Этих малых чисел может быть очень много, но на результат они все равно не повлияют, поскольку прибавляются по одному. Здесь необходимо придерживаться правила, в соответствии с которым сложение чисел нужно проводить по мере их возрастания. В машинной арифметике из-за погрешности округления существен порядок выполнения операций, и известные из алгебры законы коммутативности (и дистрибутивности) здесь не всегда выполняются.
). Этих малых чисел может быть очень много, но на результат они все равно не повлияют, поскольку прибавляются по одному. Здесь необходимо придерживаться правила, в соответствии с которым сложение чисел нужно проводить по мере их возрастания. В машинной арифметике из-за погрешности округления существен порядок выполнения операций, и известные из алгебры законы коммутативности (и дистрибутивности) здесь не всегда выполняются.
Максимальная относительная погрешность при округлении есть 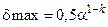 , где
, где 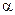 — основание системы счисления,
— основание системы счисления, 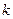 — количество разрядов мантиссы числа. При простом отбрасывании лишних разрядов эта погрешность увеличивается вдвое.
— количество разрядов мантиссы числа. При простом отбрасывании лишних разрядов эта погрешность увеличивается вдвое.
При решении задачи на ЭВМ нужно использовать подобного рода «маленькие хитрости» для улучшения алгоритма и снижения погрешностей результатов. Например, при вычислении на ЭВМ значения 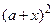 величина
величина 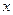 может оказаться такой, что результатом сложения
может оказаться такой, что результатом сложения 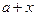 получится
получится 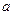 (при
(при 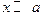 ); в этом случае может помочь замена
); в этом случае может помочь замена 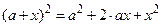 .
.
Рассмотрим еще один важный пример — использование рядов для вычисления значений функций. Запишем, например, разложение функции 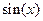 по степеням аргумента:
по степеням аргумента:
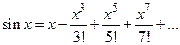
По признаку Лейбница остаток сходящегося знакочередующегося ряда, т. е. погрешность суммы конечного числа членов, не превышает значения первого из отброшенных членов (по абсолютной величине).
Вычислим значение функции 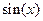 при
при 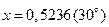 . Члены ряда, меньшие 10-4, не будем учитывать. Вычисления проведем с четырьмя верными знаками. Получим
. Члены ряда, меньшие 10-4, не будем учитывать. Вычисления проведем с четырьмя верными знаками. Получим 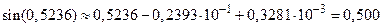 .
.
Это отличный результат в рамках принятой точности. Зная из курса высшей математики, что это разложение синуса справедливо при любом значении аргумента ( 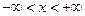 ), используем его для вычисления функции при
), используем его для вычисления функции при 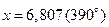 . Опуская вычисления, получаем
. Опуская вычисления, получаем 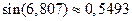 . Относительная погрешность составляет здесь около 10% (вместо ожидаемого значения 0.01% по признаку Лейбница). Это объясняется погрешностями округлений и способом суммирования ряда (слева направо, без учета величины членов).
. Относительная погрешность составляет здесь около 10% (вместо ожидаемого значения 0.01% по признаку Лейбница). Это объясняется погрешностями округлений и способом суммирования ряда (слева направо, без учета величины членов).
Ни всегда помогает и повышенная точность вычислений. В частности, для данного ряда при 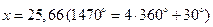 даже при учете членов ряда до 10 и вычислениях с восемью значащими цифрами в результате аналогичных вычислений (суммирование слева направо) получается результат, не имеющий смысла:
даже при учете членов ряда до 10 и вычислениях с восемью значащими цифрами в результате аналогичных вычислений (суммирование слева направо) получается результат, не имеющий смысла: 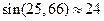 .
.
В программах, использующих степенные ряды для вычисления значений функций, могут быть приняты различные меры по предотвращению подобной потери точности. Так, для тригонометрических функций можно использовать формулы приведения, благодаря чему аргумент будет находиться на отрезке 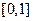 .
.
При вычислении экспоненты аргумент х можно разбить на сумму целой и дробной частей 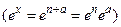 и использовать разложение в ряд только для
и использовать разложение в ряд только для 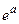 , а
, а 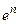 вычислять умножением.
вычислять умножением.
Таким образом, при организации вычислений можно своевременно распознать подобные «подводные камни», когда возможна потеря точности, и попытаться затем исправить положение.
Дата добавления: 2017-09-01; просмотров: 10874;










