Основные свойства векторного произведения
1. 

 = 0, если
= 0, если  и
и  - коллинеарные векторы.
- коллинеарные векторы.
Доказательство. Если векторы  и
и  коллинеарны, то sin j= 0. Следовательно, |
коллинеарны, то sin j= 0. Следовательно, |  ´
´  | = |
| = |  |·|
|·|  | sin j = 0, т. е. длина вектора
| sin j = 0, т. е. длина вектора 

 равна нулю, а значит, и сам вектор
равна нулю, а значит, и сам вектор 

 равен нулю. g
равен нулю. g
2. Длина векторного произведения неколлинеарных векторов  и
и  равна площади параллелограмма ОАВС, построенного на этих векторах
равна площади параллелограмма ОАВС, построенного на этих векторах

Доказательство: Как известно из элементарной геометрии, площадь параллелограмма равна произведению его смежных сторон на синус угла между ними. Отсюда |  |·|
|·|  | sin j = S, т. е. |
| sin j = S, т. е. |  ´
´  | = S.
| = S.
3. 

 = –
= –  ´
´  (свойство антиперестановочности сомножителей).
(свойство антиперестановочности сомножителей).
4. (λ  )
) 
 = λ (
= λ ( 

 ) (свойство сочетательности по отношению к скалярному множителю).
) (свойство сочетательности по отношению к скалярному множителю).
5. (  +
+  )
) 
 =
= 

 +
+ 

 (свойство распределительности относительно суммы векторов).
(свойство распределительности относительно суммы векторов).
6. 

 =
= 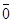 , если два ненулевых вектора коллинеарны и наооборот.
, если два ненулевых вектора коллинеарны и наооборот.
Замечание: Свойство (5) дает право при векторном умножении векторных многочленов выполнять действия почленно, а свойство 3) – объединить числовые коэффициенты векторных множителей. Например,
(2  + 3
+ 3  )
)  (4
(4  + 5
+ 5 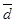 ) = (2
) = (2  + 3
+ 3  )
)  4
4  + (2
+ (2  + 3
+ 3  )
)  5
5 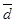 = 2
= 2 
 4
4  + 3
+ 3 
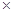 4
4  + 2
+ 2 
 5
5 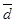 + 3
+ 3 
 5
5 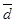 = 8 (
= 8 ( 

 ) + 12 (
) + 12 ( 

 ) + 10 (
) + 10 ( 

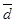 ) + 15(
) + 15(  +
+ 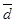 ).
).
Следует, однако, помнить, что порядок сомножителей векторного произведения является существенным и при перестановке сомножителей знак векторного произведения нужно заменить, например,
(  +
+  +
+  )
) 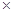 ( 2
( 2  + 3
+ 3  )= 2(
)= 2( 

 ) + 2(
) + 2( 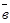

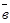 ) + 2(
) + 2( 

 ) + 3(
) + 3( 

 ) + 3(
) + 3( 

 ) + 3(
) + 3( 

 ) = 2(
) = 2( 

 ) - 2(
) - 2( 

 ) + 3(
) + 3( 

 ) +3(
) +3( 

 ) = 2(
) = 2( 

 ) + 3 (
) + 3 ( 

 ) (
) ( 

 ).
).
Замечание 2: Согласно определению и свойству 1 и 2 векторного произведения для базисных векторов  ,
,  ,
,  получаем следующие равенства
получаем следующие равенства  ´
´ 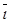 = 0 ;
= 0 ;  ´
´  =
=  ;
;  ´
´  = -
= -  ;
;  ´
´  = -
= -  ;
;  ´
´  = 0 ;
= 0 ;  ´
´  =
=  ;
;
 ´
´  =
=  ;
;  ´
´  = -
= - 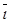 ;
;  ´
´  = 0.
= 0.
4.3. Выражение векторного произведения через координаты векторов 
Теорема: Если векторы  и
и  заданы своими координатами:
заданы своими координатами:  ={Х1 ;У1; Z1 } и
={Х1 ;У1; Z1 } и  ={Х2 ;У2; Z2 }, то векторное произведение вектора
={Х2 ;У2; Z2 }, то векторное произведение вектора  на вектор
на вектор  определяется формулой
определяется формулой
 ´
´  = { ( У1 Z2 – У2 Z1) ; (Х2 Z1 – Х1Z2) ; (Х1 У2 – Х2 У1 ) }.
= { ( У1 Z2 – У2 Z1) ; (Х2 Z1 – Х1Z2) ; (Х1 У2 – Х2 У1 ) }.
Эту формулу с помощью определителей второго порядка можно записать в виде
 ´
´  =
=  ;
;  ;
; 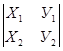
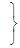 .
.
С помощью определителя третьего порядка эту формулу можно записать так:
 ´
´  =
= 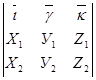 =
=  ( У1 Z2 - Z1У2) +
( У1 Z2 - Z1У2) +  (Х2 Z1 – Z2 Х1) +
(Х2 Z1 – Z2 Х1) +
+  (Х1 У2 – Х 2 У1) .
(Х1 У2 – Х 2 У1) .
Доказательство: Разложим векторы  и
и  по базису
по базису  ;
;  ;
;  ;
;  = Х1
= Х1  + У1
+ У1  + Z1
+ Z1  ,
,  = Х2
= Х2  + У2
+ У2  + Z2
+ Z2  ,
,
 ´
´  = Х1 Х2 (
= Х1 Х2 (  ´
´  ) + Х1У2 (
) + Х1У2 (  ´
´  ) +Х1 Z2 (
) +Х1 Z2 (  ´
´  ) + У1 Х2 (
) + У1 Х2 (  ´
´  ) + У1 У2 (
) + У1 У2 (  ´
´  ) + У1 Z2 (
) + У1 Z2 (  ´
´  ) + Z1 Х2 (
) + Z1 Х2 (  ´
´  ) + Z1У2 (
) + Z1У2 (  ´
´  ) + Z1 Z2 (
) + Z1 Z2 (  ´
´  ) . Отсюда на основании равенства ( 2 ), находим
) . Отсюда на основании равенства ( 2 ), находим
 ´
´  = (У1 Z2 – У2 Z1)
= (У1 Z2 – У2 Z1)  + (Х2 Z1 – Х1Z 2)
+ (Х2 Z1 – Х1Z 2)  + (Х1 У2 – Х2 У1)
+ (Х1 У2 – Х2 У1)  или
или
 ´
´  =
= 
 +
+ 
 +
+ 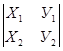
 .
.
Получено разложение вектора  ´
´  по базису
по базису  ;
;  ;
;  ; коэффициенты этого разложения представляют собой координаты вектора
; коэффициенты этого разложения представляют собой координаты вектора  ´
´  . Таким образом,
. Таким образом,  ´
´  = {Х ;У ;Z } , где Х =
= {Х ;У ;Z } , где Х =  , У =
, У =  , Z =
, Z = 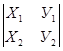 (3) . g
(3) . g
Пример: Даны векторы  = {2 ;5 ;7 }, и
= {2 ;5 ;7 }, и  = {1 ;2 ;4 }. Найти координаты векторного произведения
= {1 ;2 ;4 }. Найти координаты векторного произведения  ´
´  .
.
Решение: По формуле ( 3 ) находим Х =  = 6; У =
= 6; У = 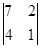 = - 1 ; Z =
= - 1 ; Z =  = – 1 .
= – 1 .
Итак,  ´
´  = {6;– 1 ; – 1}.
= {6;– 1 ; – 1}.
 § 5. Смешанное произведение векторов
§ 5. Смешанное произведение векторов
Дата добавления: 2022-02-05; просмотров: 310;










