Коммутативный закон

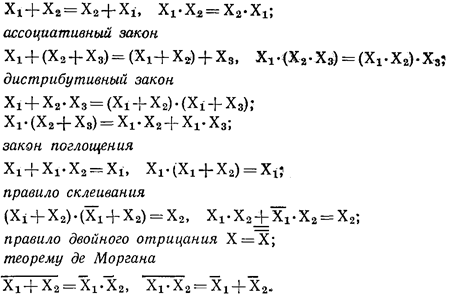
Для сложной функции правило де Моргана выглядит следующим способом:

Инверсия любого сложного выражения, в котором аргументы (или их инверсии) связаны операциями конъюнкции и дизъюнкции, может быть представлено тем же выражением без инверсии с изменением всех знаков конъюнкции на дизъюнкции, знаков дизъюнкции на конъюнкции и инверсии всех аргументов.

Например:

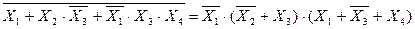
Кроме того, необходимо ставить скобки учитывая порядок действия в первом выражении.

Из правила де Моргана вытекает следствие:

Х₁×Х₂=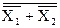

Х₁+Х₂=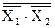

Скобки в логических выражениях определяют порядок действий, как и в обычной алгебре. При отсутствии скобок логические операции выполняются в следующем порядке:

- выполняют отрицание отдельных переменных (НЕ);

- выполняют логическое умножение (И);

- выполняют логическое сложение (ИЛИ);

- выполняют отрицание совокупности логических переменных.

Некоторые из приведённых законов не имеют аналогов в обычной алгебре чисел, например закон поглощения, теорема де Моргана, первая форма записи дистрибутивного закона. Однако, используя основные соотношения, можно доказать их справедливость. Теорема де Моргана является следствием принципа двойственности алгебры логики. Действительно, как было отмечено, если Y=X₁+Х₂, то 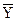= ₁• ₂. Применяя операцию инверсии к первому равенству, получаем 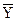= 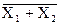. Отсюда следует 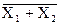= ₁• ₂. Доказательство закона поглощения можно провести с использованием второй формы записи закона дистрибутивности, а также основных соотношений:

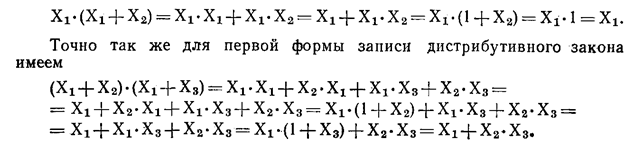
Реализация операций алгебры логики возможна, в общем случае, с помощью элементов, осуществляющих операции НЕ, ИЛИ, И. Такой набор элементов называется функционально полной системой логических элементов или логическим базисом. Однако в соответствии с принципом двойственности число необходимых элементов в такой системе можно уменьшить, исключив из нее элемент ИЛИ либо элемент И. Например, в соответствии с теоремой де Моргана имеем X₁+X₂= 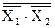. Отсюда следует, что операцию логического сложения X₁+X₂ можно заменить операцией логического умножения ₁• ₂ над инверсными значениями переменных, а затем к результату применить операцию инверсии 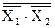и тем самым исключить элемент ИЛИ.

Следовательно, системы, состоящие из двух элементов (ИЛИ, НЕ либо И, НЕ), также являются функционально полными системами и содержат минимальный логический базис.

При схемной реализации функционально полных систем с минимальным логическим базисом идут по пути использования универсальных логических элементов.

Т.о. базис логических элементов И, ИЛИ, НЕ обладает избыточной функциональной полнотой. Для построения любой логической схемы достаточно иметь только два логических элемента: И и НЕ, либо ИЛИ и НЕ.

Такими элементами являются схемы, обеспечивающие выполнение операций ИЛИ-НЕ и И-НЕ. Элемент ИЛИ-НЕ (см. рис. а) осуществляет логическую операцию Y= 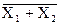, (Y=X₁¯X₂), называемую также стрелкой Пирса. Элемент И-НЕ (рис. б) осуществляет логическую операцию Y= 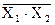(Y=X₁|X₂), называемую штрихом Шеффера.

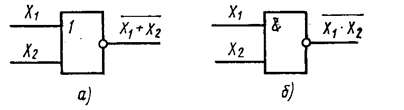
Элемент И-НЕ, так же как и элемент ИЛИ-НЕ, позволяет реализовать все три основные логические операции. Для осуществления операции НЕ с помощью элемента И-НЕ достаточно объединить входы Y= 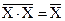(рис. а). Это же относится и к элементу ИЛИ-НЕ (Y= 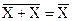). При последовательном соединении двух элементов И-НЕ, у одного из которых объединены входы (инвертор), осуществляется операция логического умножения: Y= 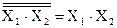(рис. б). Такое же соединение элементов ИЛИ-НЕ реализует операцию логического сложения Y= 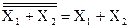. Применение трех элементов И-НЕ, два из которых работают в режиме инвертирования с объединенными входами (рис. в), позволяет реализовать операцию логического сложения Y= 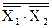=X₁+X₂. Соединение трех элементов ИЛИ-НЕ аналогично (рис. в) обеспечивает реализацию операции логического умножения Y= 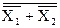=X₁×X₂.

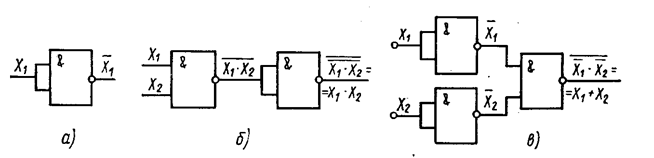
Рис. 2

Здесь следует отметить, что в соответствии с принципом двойственности элемент, осуществляющий операцию ИЛИ-НЕ в положительной логике, реализует операцию И-НЕ в отрицательной логике, и наоборот.

Таким образом, алгебра логики позволяет перейти от описательной формы представления логической функции к алгебраической и, в итоге, к схеме логического устройства.

2. Составление схем логических устройств

Логические схемы, реализованные из соединённых определённым образом между собой логических элементов, называются функциональными. Составление схемы логического устройства обычно происходит по аналитическому выражению переключательной функции, которая должна удовлетворять следующим требованиям:

- быть по возможности минимальным по числу логических операций и числу переменных;

- содержать только те логические операции, которые могут быть реализованы на имеющихся в наличии у конструктора типов ЛЭ.

Таким образом, построение логических схем по заданной функции подразумевает выполнение нескольких этапов несколько этапов:

1. От условий действия устройства, заданных словесным описанием или таблицей истинности, переходят к аналитической записи функ­ции, описывающей работу этого устройства.

2. Используя правила алгебры логики или специальные методы, минимизируют структурную формулу.

3. Приводят минимизированную формулу к форме, содержащей логи­ческие операции только заданного базиса.

4. По полученной формуле составляют функциональную и принципи­альную схемы комбинационного устройства.

В общем случае логическая функция Y может зависеть от нескольких переменных X₁, X₂, ..., Х_n. Говорят, что функция Y определена, если известны ее значения для всех возможных наборов двоичных переменных. Функция Y не определена, когда некоторые сочетания переменных по условию задачи невозможны. В этом случае функцию можно доопределить, приписав ей значение «1» либо «0» по соображениям удобства реализации.

При этом, как отмечалось ранее, функция Y может представляться в виде таблицы истинности.

Однако, определить структуру логического устройства можно, исходя из алгебраической формы записи. Для перехода от таблицы истинности к алгебраической форме записи используют совершенную конъюнктивную нормальную форму(СКНФ) либо совершенную дизъюнктивную нормальную форму(СДНФ).

СДНФ это сумма (дизъюнкция) произведений (конъюнкций) переменных для истинных, т. е. равных единице, значений функции Y.Входящие в СДНФ конъюнкции (произведения) называются минтермами (конъюнктивными термами) или конституентами единицы.

Таким образом, число слагаемых равно количеству строк таблицы истинности, в которых Y==1. Если при составлении произведения какая-либо переменная в рассматриваемой строке равна нулю, то берется ее инверсное значение.

В СДНФ функции Y нет двух одинаковых слагаемых (минтермов), а каждое слагаемое не содержит двух одинаковых множителей (логических переменных). Количество множителей во всех слагаемых одинаково и соответствует числу логических переменных (минтермы максимального ранга).

Поясним сказанное на примере таблицы истинности для трех переменных, в которой Y=1 для трех комбинаций переменных из возможных восьми (табл. 1).

Таблица 1.

В строках, для которых Y=1, значения переменных следующие:

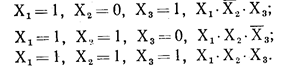
Алгебраическое выражение для функции Y в СДНФ имеет вид

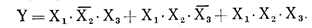(1)

СКНФ это произведение (конъюнкция) сумм (дизъюнкций) переменных для ложных, т. е. Равных нулю, значений функции Y.Входящие в СКНФ логические суммы называются макстермами (дизъюнктивными термами) или конституентами нуля.

Таким образом, порядок записи СКНФ функции Y следующий:

- записываются логические суммы переменных для строк таблицы истинности, в которых функции Y=0. Если значение переменной в строке равно 1, то в сумме записывается отрицание этой переменной;

- записывается логическое произведение составленных логических сумм.

Для получения алгебраического выражения в рассмотренном выше примере функции в СКНФ в таблице истинности выделяют строки, в которых функция Y принимает нулевые значения. Таких строк в табл. 1 пять. Затем по приведенной схеме для этих строк составляется сумма переменных величин:

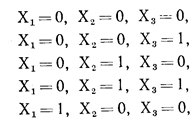
	Х1+Х2+Х3
Х1+Х2+ 3
Х1+ 2+Х3
Х1+ 2+ 3
1+Х2+Х3

Тогда в СКНФ, получаем

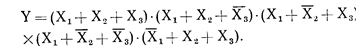(2)

Путем подстановки всех возможных комбинаций переменных нетрудно убедиться в том, что полученные алгебраические формы соответствуют табл. 1.

Соотношения (1), (2) позволяют определить структуру логического устройства, которое осуществляет операции в соответствии с приведенной таблицей истинности. Например, из формулы (1) следует, что в это устройство должны входить два инвертора (НЕ), три схемы логического умножения (И) и одна схема логического сложения (ИЛИ) (см. рис.).

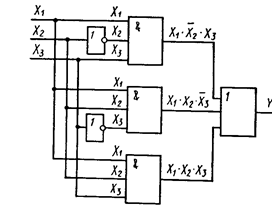
Такая структурная схема не является единственно возможной схемой логического устройства, обеспечивающего обработку информации в соответствии с приведенной таблицей истинности. Более того, она не является и оптимальной с точки зрения числа, логических элементов. Поэтому одним из важнейших этапов синтеза логических схем является минимизация числа элементов структурной схемы, что связано с минимизацией логических функций.

Минимизация осуществляется с использованием основных соотношений, законов и теорем алгебры логики. При этом широко используют следующие приемы:

прибавление одного или нескольких членов, входящих в СДНФ, поскольку Х+Х+Х=Х;

выделение членов, содержащих множитель Х+ =1;

использование правила «склеивания» и др.

При этом, для минимизации логических функций широко используется метод Квайна, который основан на использовании операций склеивания и поглощения. Он может быть применен как в случае, когда исходная формула является СДНФ функцией, так и в случае, когда исходной формулой является СКНФ функцией. Рассмотрим метод Квайна для минимизации логической формулы, заданной в виде СДНФ функции. Одна и та же конституента единицы, входящая в СДНФ, может склеиваться по разным переменным с несколькими другими конституентами единицами. Конъюнкция, получаемая в результате склеивания двух конституент единицы, называется импликантной.

Метод Квайна заключается в выполнении всех операций склеивания и поглощения с целью получения такого наименьшего набора импликант, которые совместно поглощают наибольшее число конституент единицы, входящих в исходную СДНФ функции.

Формула, полученная из СДНФ в результате выполнения всех возможных склеивании и поглощении, называется тупиковой дизъюнктивной формой функции. В общем случае выбор разных тупиковых импликант может привести к получению разных тупиковых форм. Тупиковая дизъюнктивная нормальная форма функции, содержащая наименьшее число переменных называется минимальной дизъюнктивнной нормальной формойфункции.

Например, полученную алгебраическую форму (1) можно минимизировать следующим образом

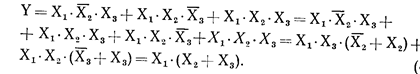3)

В результате получается более простое соотношение, реализация которого может быть осуществлена одним элементом И и одним элементом ИЛИ (см. рис.).

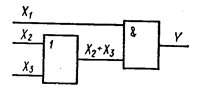
Одним из наиболее трудоемких этапов в методе Квайна является отыскание склеивающихся конституент единицы в СДНФ функции.

Для отыскания склеивающихся конституент единицы нужно первую из конституент, входящих в СДНФ предварительно сравнить со всеми остальными конституентами единицы, далее вторую конституенту единицы сравнить со всеми остальными остальными за исключением первой; третью конституенту – со всеми кроме первой и второй.

Для отыскания склеивающихся конституент единицы могут быть использованы специальные таблицы, называемые картами Карно.

Данный метод, позволяет в известном смысле автоматизировать процесс минимизации алгебраического выражения и применяется в случае небольшого числа переменных (n<6) (табл. 2).

Реализация этого метода осуществляется в несколько этапов. На первом этапе для исходной логической функции составляется карта Карно, представляющая таблицу, в верхней строке и левом столбце которой приводятся все возможные сочетания логических переменных, причем в соседних сочетаниях должна изменяться только одна переменная. Значения функции в клетках таблицы соответствуют данному сочетанию переменных.

Таблица 2

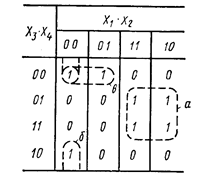
На втором этапе выделяются клетки, содержащие единицы, и осуществляется их объединение. При этом руководствуются следующими правилами: объединяются соседние клетки, в том числе и составляющие полные квадраты, полные столбцы или строки и соседние столбцы или строки. Соседними считаются также верхняя и нижняя клетки одного столбца, левая и правая клетки одной строки. Одна и та же клетка может быть объединена несколько раз: один раз с соседней клеткой в строке и другой раз — с соседней клеткой в столбце.

Следующим этапом является получение минимизированной дизъюнктивной нормальной формы (МДНФ) логической функции. С этой целью для объединенных по указанным правилам клеток составляются логические произведения, в которые входят только переменные, остающиеся неизменными для всех клеток данного объединения. Если какая-либо клетка остается необъединенной, то соответствующее ей логическое произведение содержит все переменные. Число слагаемых в МДНФ оказывается равным числу объединений и числу необъединенных клеток. Таким образом, для представленной карты Карно (табл. 2) МДНФ заданной функции Y=Х₁Х₄+ _{1 2 4}+ _{1 3 4}. Первое слагаемое соответствует объединению четырех клеток (а), второе и третье — объединению двух клеток (б и в).

Карта Карно, соответствующая таблице истинности 1, представлена в табл. 3. В ней можно выделить два объединения.

Таблица 3

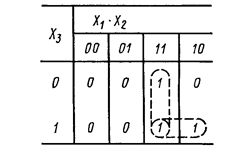
Соответствующая этим объединениям МДНФ Y=X₁X₂+X₁X₃=Х₁(Х₂+Х₃) совпадает с полученной алгебраическим методом минимизированной формой выше рассмотренного примера (3).

При схемной реализации логической функции с использованием универсальных логических элементов И-НЕ или ИЛИ-НЕ минимизированную алгебраическую форму представляют в виде комбинации операций, выполняемых этими элементами. В случае логического устройства на элементах И-НЕ осуществляют двойную инверсию исходной МДНФ и в соответствии с теоремой де Моргана получают алгебраическое выражение, в которое входят только операции И-НЕ. Например, для соотношения (3) преобразованное выражение, в которое входят только операции И-НЕ, имеет вид

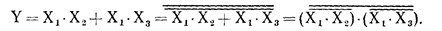
Как видно, такую функцию можно реализовать на трех универсальных элементах И-НЕ.

Таким образом, для построения схемы цифрового устройства необходимо перейти от таблицы истинности к алгебраической форме, минимизировать её и записать полученное выражение в нужном базисе.

Заключение:

1. Благодаря аппарату алгебры Буля возможен переход от описательного алгоритма функционирования цифрового устройства к аналитической форме описывающей его функции.

2. Полученная функция должна быть преобразована до тупиковой формы, после чего синтезируется цифровое устройство. При этом, необходимо обращать внимание на базис, в котором необходимо синтезировать нужное цифровое устройство.