Элементы алгебры-логики

Известно, что теоретической базой построения систем обработки информации, систем на основе ЛЭ является алгебра логики, разработанная Дж. Булем. Переменная величина Х в алгебре логики может принимать два значения: Х=1 (логическая единица) или Х=0 (логический нуль). Результат той или иной операции над одной или несколькими переменными в алгебре логики может быть представлен в виде таблицы истинности. В ней отображаются все возможные сочетания (комбинации) двоичных переменных и значения функции Y, получающиеся в результате той или иной логической операции.

Существуют три основные операции, лежащие в основе алгебры логики: инверсия (логическое отрицание), дизъюнкция (логическое сложение) и конъюнкция (логическое умножение).

Имеет место известная условность в том, какому значению переменной величины поставлен в соответствие уровень лог. «1» и лог. «0». Поэтому существуют две совершенно равнозначные (дуальные) системы с точки зрения возможности выполнения логических операций, работающие либо в положительной логике, либо в отрицательной логике. В положительной логике уровень лог. «1» соответствует высокому значению сигнала (например, напряжения), а уровень «0» — низкому значению сигнала (в частном случае его отсутствию). В отрицательной логике, наоборот, уровни лог. «1» и «0» соответствуют низкому и высокому значениям сигнала.

Имея в виду это обстоятельство, из сравнения таблицы истинности для элементов ИЛИ и И можно сделать важный вывод: операции ИЛИ (Y=X1+X2) в положительной логике соответствует операция И ( 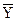= 1• 2) в отрицательной логике, и наоборот. Действительно, заменив «1» и «0» в таблице истинности элемента ИЛИ на лог. «0» и «1», т. е. осуществив инверсию переменных, получим таблицу истинности элемента ИЛИ. В этом заключается принцип двойственности алгебры логики.

Основные соотношения, правила и теоремы.Из определения логических операций инверсии, сложения и умножения вытекают следующие очевидные основные соотношения: