Ускорение жидкой частицы
Рассмотрим в качестве параметра скорость жидкой частицы  .
.
Воспользуемся формулой (4.17) и в результате получим векторную форму записи ускорения жидкой частицы.
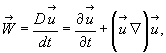 (4.18)
(4.18)
где 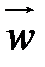 - называется субстанциональным (полным) ускорением;
- называется субстанциональным (полным) ускорением;
 - локальным ускорением;
- локальным ускорением;
( 
 )
)  - конвекторным ускорением.
- конвекторным ускорением.
Замечание:
1. Локальное ускорение определяется изменением вектора скорости в данной точке пространства.
2. Конвективное ускорение возникает вследствие того, что частица жидкости в процессе движения перемещается из данной точки в другую, в которой вектор скорости отличается от первоначального.
Из этого следует, что:
1. Если поле вектора однородно (т.е. вся жидкость перемещается поступательно как твердое тело), то конвективное ускорение равно нулю и все ускорение сводится к локальному, одинаковому во всех точках пространства, занятого движущейся жидкостью.
2. Если движение жидкости является установившимся (т.е. скорость жидкости в каждой точке не меняется с течением времени), то локальное ускорение отсутствует, а имеется лишь конвективное.
Перейдем от векторной формы записи ускорения к координатной. В результате с учетом (3.36) получим:
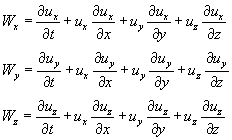 (4.19)
(4.19)
Встречается и другая векторная запись ускорения. Перепишем (4.19), заменив порядок сомножителей.

Используя формулы произведения тензора на вектор (3.4) и (3.7) и выражение дифференциального тензора векторного поля (3.42) и (3.45), можно представить вектор ускорения в следующей компактной форме:
 (4.20)
(4.20)
где
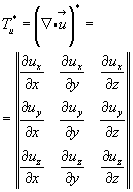
Для исследования (изучения) вихревого движения выражение (4.20) для ускорения следует преобразовать, вводя компоненты вихря.
В соответствии с равенством (3.11) разложим тензор Tu* на симметричную и антисимметричную часть
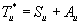 (4.21)
(4.21)
причем, как это следует из (4.8)


из выражения (3.34) следует, что:
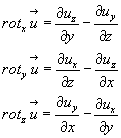
Поэтому тензор Аu можем переписать в следующем виде:
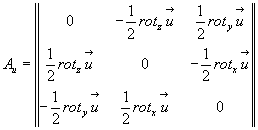 (4.22)
(4.22)
Умножим дифференциальный тензор Tu* поля вектора  на произвольный вектор
на произвольный вектор  с проекциями Nx, Ny, Nz. Очевидно, что
с проекциями Nx, Ny, Nz. Очевидно, что
 (4.23)
(4.23)
Представим произведение Аu  в развернутом виде. В соответствии с (3.3) и (4.22) можем записать:
в развернутом виде. В соответствии с (3.3) и (4.22) можем записать:
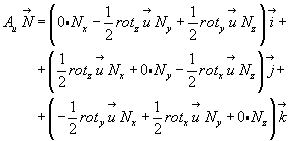 (4.24)
(4.24)
Этот же вектор Аu  представим в другой форме. Для этого запишем (определим) векторное произведение rot
представим в другой форме. Для этого запишем (определим) векторное произведение rot  на
на 
 (4.25)
(4.25)
Сравнивая выражения (4.24) и (4.25), убеждаемся в справедливости тождества
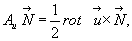 откуда
откуда
прямо следует формула Гельмгольца
 (4.26)
(4.26)
Рассмотрим произведение дифференциального тензора поля вектора  на тот же вектор
на тот же вектор  .
.
Представим в развернутом виде одну из проекций вектора Tu*  , например на ось Оx. В соответствии с (3.46) с (3.33) получим:
, например на ось Оx. В соответствии с (3.46) с (3.33) получим:
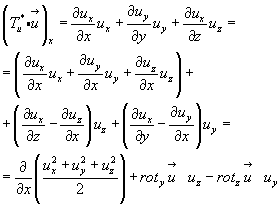 (4.27)
(4.27)
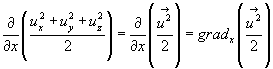
Кроме этого, как видно из формулы (4.25),


следовательно,
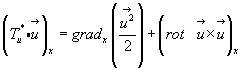 (4.28)
(4.28)
Аналогичные равенства можно записать и для остальных проекций, откуда следует справедливость векторного равенства
 (4.29)
(4.29)
называемого формулой Ламба-Громски
Т.о. из формул (4.29) и (4.20) находим выражение для ускорения в форме Ламба-Громски, которое широко используется при анализе уравнений гидродинамики
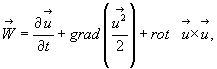 (4.30)
(4.30)
Замечание:
Такая форма записи ускорения указывает на наличие или отсутствие вихрей и позволяет установить различие в особенностях вихревого и безвихревого движений жидкости.
Дата добавления: 2019-12-09; просмотров: 719;