Архимедовская расположенность полукольца натуральных чисел.
Теорема 11. Полукольцо натуральных чисел является архимедовски расположенным, т.е. выполняются следующее условие (аксиома Архимеда): для любых натуральных чисел a,b a<nb для некоторого натурального n.
Доказательство.
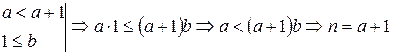 .
.
что и требовалось доказать.
Теорема 12. Полукольцо натуральных чисел не является всюду плотным.
Доказательство.
Для доказательства этого утверждения достаточно показать, что натуральные числа 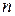 и
и 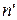 являются соседними. Предположим обратное: пусть
являются соседними. Предположим обратное: пусть 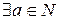 такое, что
такое, что 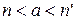 . Тогда
. Тогда 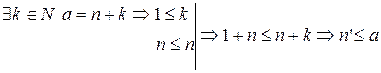 . Последнее противоречит условию
. Последнее противоречит условию 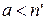 . Следовательно, предположение неверно.
. Следовательно, предположение неверно.
что и требовалось доказать.
Лекции 3-4.
Построение множества целых чисел.
Рассмотрим множество 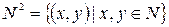 (декартов квадрат множества натуральных чисел).
(декартов квадрат множества натуральных чисел).
На множестве 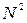 введем отношение ~ по следующему правилу:
введем отношение ~ по следующему правилу:
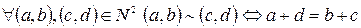 .
.
Теорема 1. Отношение ~ на множестве 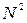 есть отношение эквивалентности (рефлексивно, симметрично, транзитивно).
есть отношение эквивалентности (рефлексивно, симметрично, транзитивно).
Доказательство.
Отношение ~ рефлексивно (?)
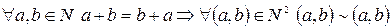 .
.
Отношение ~ симметрично (?)
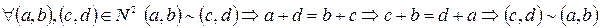 .
.
Отношение ~ транзитивно (?)
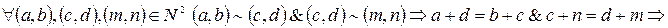
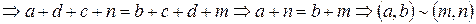 .
.
что и требовалось доказать.
Поскольку отношение ~ является отношением эквивалентности, имеют место классы эквивалентности:
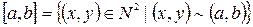 .
.
Определение. Целыми числами назовем элементы фактормножества 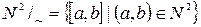 .
.
Дата добавления: 2022-04-12; просмотров: 233;