Упругая система станка
С точки зрения динамики реальная упругая система станка ‑ это сложная колебательная система с распределенными инерционными и упругими параметрами, имеющая большое число степеней свободы и соответственно большое множество собственных частот колебаний. Характеристики УС определяются следующими основными параметрами: массами и моментами инерции узлов и деталей; жесткостью упругих элементов; силами неупругого сопротивления (демпфирования); связями между перемещениями масс в системе со многими степенями свободы.
Массы и моменты инерции узлов и деталей станка определяются как расчетом (по чертежам), так и экспериментально. Методы их определения приведены в соответствующей справочной литературе.
Жесткости различных конструктивных элементов определяются известными методами механики. Жесткость стыка зависит от величины предварительного натяга в соединении и действующих нагрузок, поэтому ее следует рассматривать в рабочем и относительно узком диапазоне нагружения стыка. Методы определения жесткости конструктивных элементов и стыков металлорежущих станков приведены в специальной литературе.
Силы неупругого сопротивления или силы демпфирования в элементах станка определяются рассеиванием энергии в деформируемом материале и трением в стыках деталей.
В многомассовых колебательных системах перемещения отдельных масс связаны друг с другом. Связи могут быть статическими (упругими), скоростными и инерционными. Статические связи вызывают деформацию элемента системы по координатам. Скоростные связи создают зависимые перемещения узла по координатам. Инерционная связь получается при действии сил инерции в направлении жесткости системы.
При расчете динамических характеристик реальную УС станка заменяют расчетной схемой, т.е. системой с конечным числом степеней свободы. Расчетная схема должна быть, с одной стороны, эквивалентна реальной системе станка с достаточной для практики точностью, с другой – максимально проста и сведена к минимальному количеству сосредоточенных масс.
Расчетная схема упругой системыстанка представляется в виде некоторого количества сосредоточенных масс, соединенных упругими и диссипативными (рассеивающими энергию колебаний) элементами, обычно с линейными характеристиками. Такое представление системы станка основано на том, что большинство корпусных деталей - тяжелые и относительно жесткие тела, а деформации сосредоточены в основном в стыках. Разумеется, там, где нельзя пренебречь распределенностью параметров, например, при расчете шпиндельного узла, это учитывают в виде упругих элементов (стержней, пластин и т.д.) с сосредоточенными инерционными параметрами.
Разработку расчетной схемы УС можно проводить на основе чертежей станка или экспериментальных данных, полученных для базового варианта станка, что позволяет при разработке расчетной схемы сделать ряд обоснованных упрощений и существенно сократить в дальнейшем объем расчетных работ.
В качестве примера рассмотрим построение расчетной схемы УС вертикально-сверлильного станка (рис. 3) по связи с процессом резания.
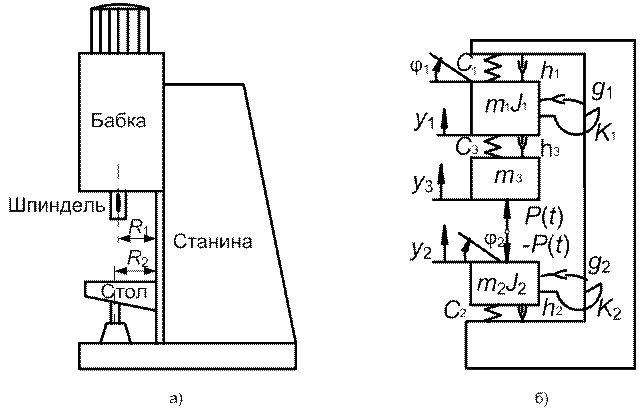
Рис. 3. Пример компоновки (а) и расчетной схемы (б) станка.
Предварительные эксперименты по определению форм колебаний УС показали слабую взаимосвязь колебаний станка по различным координатным осям и дают основание рассматривать его упругую систему как плоскую, состоящую из двух ветвей: шпиндель – шпиндельная бабка – стойка – основание и стол – основание. Собственные деформации корпусных деталей существенно ниже деформации стыков, поэтому их можно рассматривать как абсолютно жесткие тела.
Массивы представляются в виде сосредоточенных масс mi и моментов инерции Ji, жесткость площадок контакта определяет линейную Сi и изгибную (угловую) Ki жесткость стыка. Диссипативные связи, определяющие демпфирование колебаний УС, представлены как линейные hi или изгибные (угловые) gi в зависимости от формы колебаний.
Таким образом, в данном примере расчетная схема УС вертикально-сверлильного станка содержит пять сосредоточенных масс и моментов инерции, соединенных упругими и диссипативными связями. Нас интересуют колебания в направлении оси Y, т.е. в направлении изменения толщины срезаемого слоя.
На основании расчетной схемы составляется динамическая (математическая) модель компоновки. Модель может быть получена известными из теоретической механики методами, например, с использованием принципа Д’Аламбера, и представляет собой систему дифференциальных уравнений:
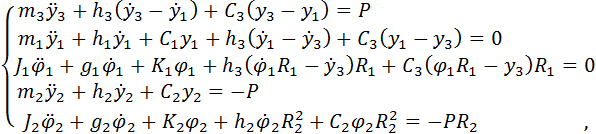
|
где 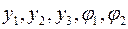 – линейные и угловые деформации элементов компоновки;
– линейные и угловые деформации элементов компоновки; 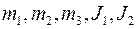 – массы и моменты инерции узлов;
– массы и моменты инерции узлов; 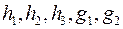 – линейные и угловые диссипативные связи (демпфирование);
– линейные и угловые диссипативные связи (демпфирование); 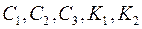 – линейные и угловые жесткости стыков;
– линейные и угловые жесткости стыков; 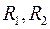 – плечи действия сил на элементы компоновки относительно стыков "шпиндельная бабка – стойка" и "стол – стойка";
– плечи действия сил на элементы компоновки относительно стыков "шпиндельная бабка – стойка" и "стол – стойка"; 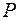 – внешняя сила, действующая на станок.
– внешняя сила, действующая на станок.
Полученная математическая модель может быть решена известными в математике способами или с использованием методики теории автоматического управления, в частности, методы с использованием частотных характеристик и переходных процессов.
Частотные характеристики упругой системы. Для определения частотных характеристик системы следует сделать с уравнениями преобразование Лапласа и, сгруппировав коэффициенты относительно переменных, получим систему уравнений в операторной форме записи:

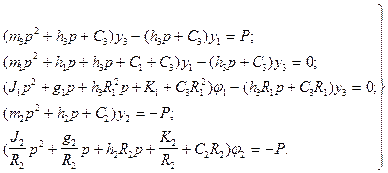
Деформация УС в зоне резания определяется алгебраической разностью деформаций шпиндельного узла 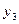 и стола с обрабатываемой деталью
и стола с обрабатываемой деталью 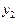 :
:
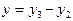 ,
,
которые можно определить, используя теорему Крамера. С этой целью уравнения записываются в полном виде и в каждом содержатся все переменные в одинаковой последовательности, при этом некоторые переменные, которые не входили в систему математической модели, будут иметь коэффициент равный 0.
Интересующие нас определители формируются следующим образом. Главный определитель 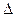 формируется из коэффициентов левых частей полной системы уравнений, частные определители
формируется из коэффициентов левых частей полной системы уравнений, частные определители 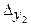 и по координатам
и по координатам 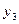 и
и 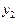 составляются из главного заменой коэффициентов в главном определителе на свободные члены уравнений (правая часть уравнений).
составляются из главного заменой коэффициентов в главном определителе на свободные члены уравнений (правая часть уравнений).
Перемещения 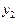 и
и 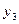 определяются отношением соответствующих определителей
определяются отношением соответствующих определителей
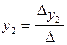 и
и 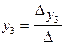
Вычислив определители известным способом, можно получить передаточную функцию УС:
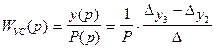
Приравняв в этом выражении оператор 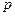 =0, получим выражение статической характеристики (податливости) упругой системы
=0, получим выражение статической характеристики (податливости) упругой системы 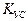 .
.
Частотные характеристики УС определяются из передаточной функции Wyс(р) заменой оператора р на комплексную переменную jω. Выделив известными методами в полученном выражении вещественную и мнимую части, получим комплексную частотную характеристику
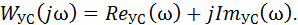
При необходимости можно получить математические выражения для амплитудной Aус(ω) и фазовой φус(ω) частотных характеристик,:
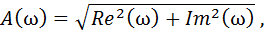
| |
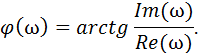
|
Используя эти характеристики можно построить АФЧХ упругой системы.
На рис. 4 показаны примеры АЧХ и АФЧХ упругой системы станка в рабочем диапазоне частот, т.е. в частотном диапазоне действующих на УС нагрузок.
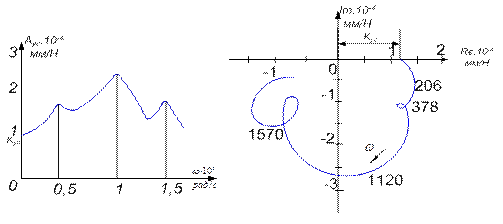
Рис. 4. Амплитудная и комплексная частотные характеристики УС станка
Отрезки, расположенные на оси ординат АЧХ и на положительной ветви вещественной оси АФЧХ для частоты ω = 0, соответствуют значению статической характеристики Kус, представляющей собой суммарную податливость упругой системы станка. Значение статической характеристики можно получить из выражения передаточной функции УС, приравняв к нулю комплексную переменную р=0:
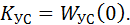
Частотные характеристики УС полезны для определения собственных частот колебаний станка и управления спектром частот при отстройке системы от резонансных явлений. Однако основное, для чего необходимы частотные характеристики УС, это определение устойчивости работы станка на том или ином режиме т.е. в процессе резания, позиционирования рабочего органа и т.д.
Определение рациональных путей улучшения характеристик упругой системы возможно лишь при рассмотрении ее в совокупности с рабочими процессами станка.
Процесс резания
Процесс резания представляет собой элемент динамической системы станка, входным параметром которого является относительное смещение инструмента и заготовки, а выходным – сила резания, действующая на УС. Существенное влияние на изменение силы резания оказывают изменения сечения срезаемого слоя и геометрии резания, что наблюдается при смещении инструмента и заготовки по оси Y. Кроме того, деформация УС в этом направлении приводит к снижению точности обработки (например, относительное смещение резца и заготовки по оси Y приводит к изменению диаметра обрабатываемой поверхности на токарном станке). Эти обстоятельства обуславливают определение характеристик элемента ПР по связи с деформацией УС в направлении оси Y.
Силу резания Р можно выразить известной в теории резания зависимостью
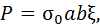
|
где σ0 – коэффициент, учитывающий механические свойства обрабатываемого материала, МПа; а и b – толщина и ширина срезаемого слоя соответственно, мм; ξ – коэффициент усадки стружки. Коэффициент σ0 зависит от временного сопротивления обрабатываемого материала σв. Для малых передних углов резца условное напряжение σ0 принимают равным
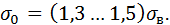
Учитывая малые смещения УС при колебаниях, можно принять в приращениях Δа = у и выражение для силы резания записать в виде
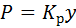 ,
,
где Кр – коэффициент резания (статическая характеристика ПР), Н/мм; у – деформация УС по нормали к поверхности резания, мм.
Коэффициент резания Кр (или коэффициент «жесткости» резания) представляет собой практически стабильную величину для конкретных условий обработки:
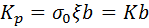 .
.
Коэффициент K – удельная сила резания, зависящая от обрабатываемого материала: для литейных чугунов К = 0,8 кН/мм2; для конструкционных сталей К = 2,0 кН/мм2; для легированных сталей К = 2,5...3,0 кН/мм2.
Опираясь на современное учение о резании металлов, можно показать, что физические явления, возникающие в процессе стружкообразования, приводят к смещению во времени изменения силы резания по отношению к вызвавшему это изменение фактору. Это отставание во времени наглядно прослеживается при ступенчатом изменении толщины срезаемого слоя. На рис. 5 схематично показаны последовательные стадии положения резца при его врезании в заготовку и формирование стружки, а также соответствующие этим положениям значения силы резания Р.
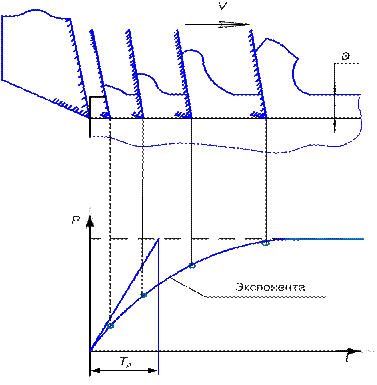
Рис. 5. Формирование стружки и силы резания при врезании
С достаточной для практических целей точностью можно принять закон изменения силы резания при ступенчатом изменении толщины срезаемого слоя экспоненциальным, т.е. инерционность, которая определяется ограниченностью скорости нагружения деформируемого объема металла, характеризуется постоянной времени стружкообразования ТР. Представив ПР инерционным элементом динамической системы станка (используя метод идентификации), можно записать уравнение, описывающее поведение этого элемента:
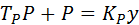
или в операторной форме записи
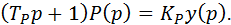
|
Постоянная времени стружкообразования ТP зависит от геометрии инструмента, обрабатываемого материала, толщины срезаемого слоя и скорости резания:
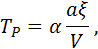
где α – коэффициент пропорциональности, зависящий от обрабатываемого материала и условий резания; V – скорость резания, мм/с.
Физический смысл произведения αaξ = lP – «длина пути стружкообразования», т.е. расстояние, проходимое резцом относительно обрабатываемой поверхности для формирования стружки и, следовательно, силы резания.
Передаточная функция элемента WP(p) ПP определяется на основе приведенных выражений отношением силы резания Р(р) к деформации УС у(р)
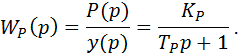
|
Комплексная частотная характеристика получается заменой в выражении передаточной функции комплексной переменной р на её значение jω (1.3):
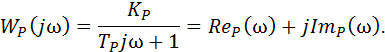
Имея эти выражения, можно при необходимости построить амплитудную и фазовую частотные характеристики ПР. На риc. 6 показана комплексная частотная характеристика ПР для стационарного режима обработки при значении параметров: КP = 700 Н/мм, ТP = 0,3∙10-4 с.
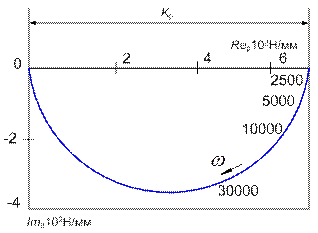
Рис. 6. АФЧХ процесса резания
Как видно из графика, АФЧХ процесса резания расположена в одном квадранте.
Процесс трения
При нормальной эксплуатации металлорежущих станков перемещение узлов в зависимости от типа направляющих протекает в режиме трения скольжения (смешанного или жидкостного) или трения качения. Неустойчивость движения ползуна (фрикционные автоколебания) наблюдается на направляющих скольжения смешанного трения. Жидкостное трение и трение качения обычно не вызывают скачкообразного движения узла в силу их низкого и относительно стабильного коэффициента трения.
Процесс трения характеризуется коэффициентом трения μ - отношение силы трения F к нормальной нагрузке N. Значения коэффициентов трения скольжения для различных фрикционных пар приведены в соответствующей справочной литературе.
В статической форме сила трения определяется законом Кулона
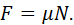
Выразив нормальную нагрузку через деформацию контактирующих поверхностей, получим уравнение для силы трения в отклонениях
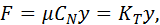
где СN – коэффициент жесткости контактирующих поверхностей по нормали к поверхности трения, Н/мм; у – контактная деформация, мм.
Коэффициент пропорциональности Кт между силой трения и контактной деформацией УС называется статической характеристикой процесса трения
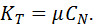
При соприкосновении поверхностей под нагрузкой происходит вдавливание контактирующих неровностей друг в друга. Тангенциальное смещение формирует в зоне контакта напряженное состояние, перед выступом образуется волна, препятствующая движению (рис. 7).
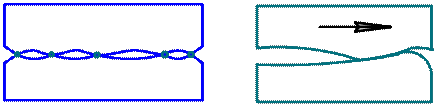
Рис. 7. Схемы реального контактирования поверхностей трения
и деформирования поверхностного слоя
Высота волны зависит от глубины внедрения выступа в сопрягаемое тело, т.е. от величины нормальной нагрузки, формы выступа и твердости фрикционных поверхностей. В процессе смещения волна растет, вместе с ней растет сила сопротивления движению (сила трения) до тех пор, пока «вспученный» металл не начнет продавливаться под выступ (упругое оттеснение).
В процессе предварительного смещения, пока не началось скольжение, имеем стык, обладающий определенной тангенциальной жесткостью. Это обстоятельство в совокупности с образованием волны определяет отставание во времени формирования силы трения от изменения нормальной силы. Если ступенчато изменить нормальную силу N, приложенную к ползуну (рис. 8, а), сила трения изменяется по закону, близкому к экспоненциальному (рис. 8, в).
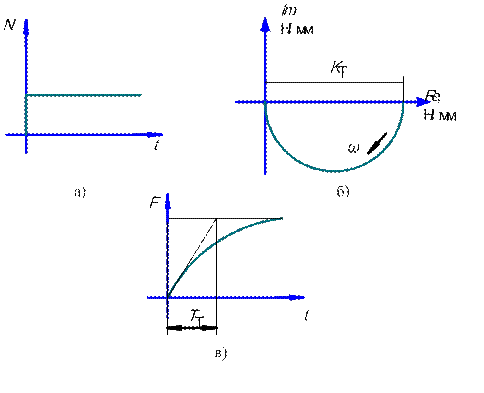
Рис. 8. Изменение силы трения при ступенчатом изменении нормальной
силы и комплексная характеристика процесса трения
По аналогии с процессом резания передаточную функцию WT(p) процесса трения как инерционного звена системы можно представить в виде
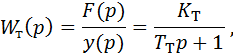
где F(p) и у(р) – лапласовы изображения силы трения и нормального смещения ползуна; Тт – постоянная времени предварительного смещения, с.
Постоянная времени может быть представлена как отношение некоторой части предварительного смещения lT к скорости скольжения V, которая предполагается постоянной (среднее значение)
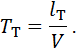
Постоянная времени предварительного смещения может составлять величину от сотых долей секунды до целых секунд в зависимости от материалов фрикционных пар, нормальной нагрузки, типа смазки и т.д. Например, для фрикционной пары чугун-чугун и смазки индустриальным маслом при скорости скольжения 0,1 мм/с постоянная времени составляет примерно 0,001 с. Достоверные значения этого параметра получают экспериментально.
Амплитудно-фазовая частотная характеристика ПТ показана на рис. 8, б и имеет выражение
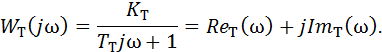
Приведенные зависимости статической и динамических характеристик процесса трения справедливы в линейной постановке задачи, когда скорость возможных колебаний ползуна по координате движения не будет превышать значение скорости скольжения, т.е. сформировавшееся при предварительном смещении напряженное и деформационное состояние поверхностей трения изменяется незначительно. Если это условие не выполняется, то движение ползуна происходит с остановками (релаксационные автоколебания) и сила трения будет изменяться от значения трения скольжения до нуля или даже принимать отрицательное значение. Эти изменения происходят по форме гистерезиса, т.е. в нелинейном виде.
Дата добавления: 2020-10-14; просмотров: 632;