ЗАКОНОМІРНОСТІ ВІЛЬНОГО РУХУ ТІЛ У СЕРЕДОВИЩІ
Вільним називається падіння окремих ізольованих одна від одної частинок у необмеженому об’ємі середовища.
Швидкість вільного падіння тіл у середовищах визначається взаємодією сил:
- гравітаційної
F1 = πd3 (δ – Δ) g / 6, Н, (2.1)
- гідродинамічного опору
F2 = ψV2d2Δ , Н, (2.2)
де d – еквівалентний діаметр кулі рівновеликої за об’ємом реальному тілу, м; δ – густина тіла, кг/м3; Δ–густина середовища, кг/м3; g – прискорення вільного падіння, м/с2; ψ–коефіцієнт гідродинамічного опору середовища рухомому тілу; V- швидкість тіла в середовищі, м/с.
Сила опору середовища рухомому в ньому тілу залежить від режиму руху – ламінарного або турбулентного. Режим руху характеризується безрозмірним параметром – числом Рейнольдса:
Re = VdΔ /μ , (2.3)
де μ – динамічний коефіцієнт в’язкості, Па • с.
Ламінарний режим обтікання відбувається при невеликих швидкостях руху (Re <1) частинок малої крупності (d < 0,1 мм). У цьому випадку сила в’язкісного опору середовища обумовлюється силами тертя і описується законом Стокса:
F2• = 3πμVd.(2.4)
Якщо динамічний коефіцієнт в'язкості μ представити з використанням формули (2.3), то рівняння (2.4) можна перетворити в такий спосіб:
F2• = 3πV2d2Δ / Re . (2.5)
Турбулентний режим обтікання характерний для високих швидкостей руху (Re >1000) великих частинок (d > 2 мм). Турбулентне обтікання супроводжується утворенням вихорів за рухомим тілом, інерційний опір середовища рухомому тілу описується законом Ньютона-Ріттінгера:
F2•• = πV2d2Δ / 16. (2.6)
Тіло випробовує одночасно вплив двох опорів, але в різному ступені. При параметрах Рейнольдса Re <1 переважає дія сил в'язкості, при параметрах Рейнольдса Re >1000 переважає дія сил інерції.
Для проміжної області значень параметра Рейнольдса 1 ≤ Re ≤ 1000, що відповідають швидкостям руху частинок крупністю 0,1 ≤ d ≤ 2 мм, Аллен запропонував визначати опір тілу за формулою:
F2•••= 5πV2d2Δ / (8 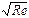 ) . (2.7)
) . (2.7)
При цьому коефіцієнт гідродинамічного опору середовища залежно від режиму руху приймає значення:
ψ = π / 16– рух у турбулентній області; (2.8)
ψ = 5π / (8 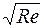 ) – рух у проміжній області; (2.9)
) – рух у проміжній області; (2.9)
ψ = 3π / Re – рух у ламінарній області. (2.10)
 У результаті узагальнення експериментальних даних Релеєм була отримана діаграма ψ = f (Re) для різних режимів руху кулястих тіл у різних середовищах (рис. 2.1), але для практичних цілей застосувати діаграму Релея досить складно.
У результаті узагальнення експериментальних даних Релеєм була отримана діаграма ψ = f (Re) для різних режимів руху кулястих тіл у різних середовищах (рис. 2.1), але для практичних цілей застосувати діаграму Релея досить складно.
Аналітичний вираз для визначення швидкості руху тіла в середовищі з урахуванням основних сил – гравітаційної (2.1) і опору (2.2), може бути отриманий з рівняння:
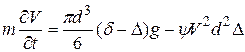 . (2.12)
. (2.12)
При m = πd3δ/6 прискорення падаючого в середовищі тіла складає:
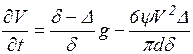 , м/с2 . (2.13)
, м/с2 . (2.13)
Спочатку (протягом часу t0) тіло рухається в середовищі прискорено:
t0 = 2,5 V0 / g0 , с, (2.14)
де V0– кінцева швидкість руху тіла, м/с; g0 – початкове прискорення, м/с2:
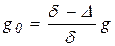 , м/с2 . (2.15)
, м/с2 . (2.15)
За час t0 тіло проходить шляхL0:
L0 = 1,8 V02 / g0 ,м . (2.16)
Після закінчення проміжку часу t0 настає рівновага сил, прискорення тіла дорівнює нулю і тіло рухається рівномірно зі швидкістю V0 = const, що називається кінцевою швидкістю вільного падіння:
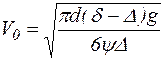 , м/с. (2.17)
, м/с. (2.17)
З урахуванням коефіцієнта опору ψ (2.8) – (2.10) можуть бути отримані вирази для визначення швидкості руху тіл у різних режимах.
Дата добавления: 2016-07-22; просмотров: 1484;