Изменение скорости и направления ветра под влиянием силы трения

Влияние силы трения сказывается на отклонении скорости и направления ветра от их градиентных значений. В прилегающем к земной поверхности слое атмосферы толщиной в несколько десятков метров (в приземном слое) турбулентный обмен количеством движения настолько велик, что направление ветра с высотой практически остается неизменным. В этом слое сила турбулентного трения с высотой не изменяется, что является физическим определением приземного слоя. Это равнозначно пренебрежению всеми силами, кроме силы трения.

Естественно, что движение в этом слое происходит не за счет воздействия пассивной силы, однако его закономерность определяется ею. Воздух в этом слое перемещается под влиянием барического градиента, действующего в вышележащих слоях. Воздух, движущийся внизу, как бы тащится вышележащим потоком, отставая от него.

Ориентируя ось х по направлению ветра, напишем формулу (13, 17) в следующем виде:

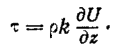
Будем считать, что в пределах приземного слоя атмосферы р = const, т. е. не зависит от высоты. Кроме этого, примем, что коэффициент турбулентности к (z) линейно возрастает с высотой, т. е.

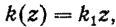
где k₁ — коэффициент турбулентности, относящийся к фиксированному уровню, например высоте в 1 л над поверхностью Земли.

После этого формулу (13, 17) можно написать в следующем виде:

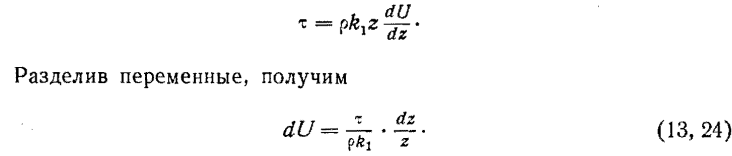
Примем следующие граничные условия: U = 0 на высоте z₀. Это значит, что существует такой тонкий слой атмосферы, в котором в результате трения о земную поверхность средняя скорость ветра равна нулю (воздух прилипает к земной поверхности). Непосредственную проверку этой гипотезы осуществить очень трудно, однако дальнейшие выводы с принятием этой гипотезы дают результаты, соответствующие опыту. Косвенные экспериментальные, данные показывают, что величина z₀ не превышает нескольких сантиметров.

Проинтегрируем уравнение (13, 24) с учетом принятых граничных условий

Таким образом, средняя скорость ветра в приземном (приводном) слое атмосферы увеличивается с высотой пропорционально логарифму последней. Мгновенные же значения скорости ветра под влиянием турбулентности будут испытывать беспорядочные, случайные колебания, аналогичные колебаниям температуры воздуха, описанным в гл. 10.

Формула (13, 25) справедлива для условий однородной атмосферы, когда турбулентность образуется лишь за счет сил трения. В действительности на развитие турбулентности большое влияние оказывают гидростатические силы, которые мы оцениваем по устойчивости стратификации атмосферы. С учетом действия этих сил изменение ветра с высотой, по данным последних исследований, выражается следующей формулой:

Таким образом, учет влияния гидростатических сил в формуле (13, 26) производится с помощью масштаба длины, который является функцией потока тепла, т. е. количества тепла, протекающего через единичную горизонтальную площадку в единицу времени.

При устойчивой стратификации поток тепла направлен вниз (р < 0), L > 0. При неустойчивой стратификации поток тепла направлен вверх (р > 0), L < 0.

Из этой формулы после интегрирования получим тот же логарифмический закон ветра, выведенный ранее иным способом. Над морями в приводном слое атмосферы изменение ветра с высотой выражается формулой

Здесь U_n — скорость ветра на фиксированном уровне, высотой n метров.

Производная от скорости ветра по логарифму высоты (логарифмический вертикальный градиент) является переменной величиной, зависящей от динамической и термической турбулентности. Динамическая турбулентность определяется средней скоростью ветра. При установившемся волнении моря ею же определяется и шероховатость морской поверхности. Термическая турбулентность определяется стратификацией воздушной массы, а последняя в приводном слое атмосферы зависит в основном от разности температур воды и воздуха.

Таким образом, производная скорости ветра по логарифму высоты определяется средней скоростью ветра и разностью температур между водой и воздухом. График такой зависимости приведен на рис. 116.

Из этого графика видно, что с увеличением разности температур воды и воздуха от -5° до +5° вертикальный градиент ветра уменьшается в 2,2 раза, а при изменении скорости ветра на 6 м/сек он изменяется в 1,6 раза. Отсюда следует, что вклады термического и динамического факторов в развитие турбулентности имеют величины одного порядка.

Как и следовало ожидать, при отрицательных разностях температур вода — воздух турбулентность ослаблена, поэтому ветер с высотой изменяется быстро, при положительных разностях турбулентность развита сильнее и ветер падает медленно.

Несколько неожиданны зависимости вертикальных градиентов скорости ветра от среднего значения скорости ветра по данным нашего графика. При отрицательных значениях разности температур вода — воздух с увеличением скорости ветра до 8 м/сек вертикальный градиент скорости ветра уменьшается, что указывает на увеличение турбулентности, а с дальнейшим увеличением скорости ветра его вертикальные градиенты увеличиваются, следовательно, турбулентность уменьшается.

При положительных значениях разности температур воды и воздуха градиенты скорости ветра увеличиваются с увеличением средней скорости ветра, что указывает на уменьшение турбулентности. Эти положения вытекают и из обработки данных по вертикальному распределению влажности воздуха, а также и самих коэффициентов турбулентности. Наиболее вероятным объяснением такой закономерности является то обстоятельство, что над морем из-за подвижности подстилающей поверхности вследствие морских течений и волнения мы имеем дело с относительной скоростью ветра, являющейся разностью между скоростью движения воздуха и воды.

Изложенные здесь закономерности вертикального распределения скорости ветра в приземном слое атмосферы справедливы для тех случаев, когда вертикальное распределение ветра и температуры воздуха описывается плавными кривыми, т. е. приземный слой квазистационарен. В действительности это бывает не всегда. На границах теплых и холодных течений плавность хода кривых может отмечаться лишь в очень тонком слое порядка нескольких метров, а далее кривые претерпевают разрыв. Такое же положение наблюдается при смене направления ветра, резком изменении его скорости во времени или при наличии упорядоченных вертикальных движений воздуха. В таких случаях приземный слой нельзя считать установившимся и все приведенные формулы пригодны лишь до уровня, где имеется плавный ход метеорологических элементов по высоте.

Влияние сил турбулентного трения распространяется и за пределы приземного (приводного) слоя атмосферы. Однако с высотой оно уменьшается, поэтому наряду с силой трения начинают действовать и другие силы и прежде всего отклоняющая сила вращения Земли. В связи с действием силы Кориолиса над приземным слоем атмосферы с увеличением высоты изменяется не только скорость, но и направление ветра.

Данные наблюдений показывают, что наземный ветер отклоняется от градиентного в сторону градиента давления на величину порядка 20—30°. Как и следовало ожидать, это отклонение над гладкой, например морской поверхностью, меньше, чем над неровной. По мере увеличения высоты истинный ветер, усиливаясь, по направлению приближается к градиентному. При этом характерно, что истинный ветер в нижних слоях по скорости приближается к градиентному раньше (ниже), чем по направлению. Изменение ветра с высотой зависит от кривизны изобар: в циклоне истинный ветер приближается к градиентному на более низком уровне, чем в антициклоне. Это согласуется с тем, что у земной поверхности в циклоне истинный ветер отклонен от градиентного меньше (15—20°), чем в антициклоне (30—35°).

Слой атмосферы, в котором из-за трения ветер отклоняется от градиентного, называется пограничным слоем. Исходя из профиля ветра, академиком Н. Е. Кочиным предложен следующий критерий для определения высоты пограничного слоя атмосферы:

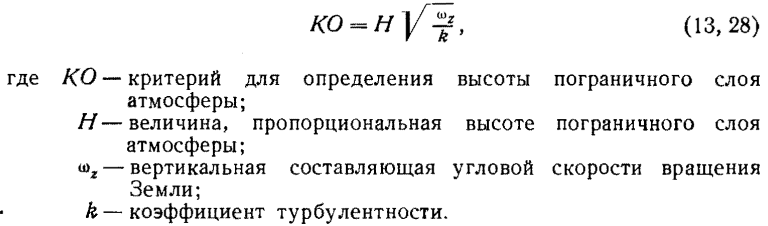
В том случае, когда КО в несколько раз превосходит единицу и ветер приближается к градиентному, действием турбулентных сил трения можно пренебрегать.

Вычисления по формуле (13, 28) показывают, что пограничный слой распространяется до высот 500—1000 м. Однако при этом не учитывается действие гидростатических сил, которые либо повышают, либо понижают высоту пограничного слоя атмосферы.

Из формулы (13, 28) следует, что высота пограничного слоя увеличивается с увеличением турбулентности, т. е. над морем летом она меньше, чем зимой, а над континентом летом больше, чем зимой.

К настоящему времени имеется много попыток математического решения уравнений движения для пограничного слоя атмосферы. Во всех случаях уравнения типа (13, 18) решаются при условии, что движение считается установившимся. Наиболее характерным различием этих решений является выбор математической модели для изменения коэффициента турбулентности с высотой. Наиболее распространенной моделью является линейно-ломаный профиль коэффициента турбулентности. Сущность этой модели сводится к тому, что в пределах приземного слоя атмосферы k = k₁z, а за пределами этого слоя высотой h k = k₁h, т. е. коэффициент турбулентности остается неизменным.

Если направление оси х подобрать совпадающим с направлением градиентного ветра U_g, а направление оси у совпадающим с направлением горизонтального градиента давления, то решения уравнений (13, 18) получаются в следующем виде:

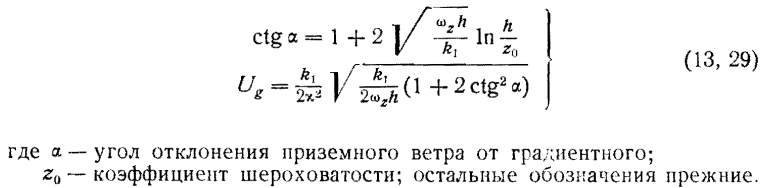
Из формулы (13,29) следует, что ветер отклоняется от градиентного тем больше, чем больше коэффициент турбулентности и коэффициент шероховатости. Кроме этого, большим высотам приземного слоя атмосферы соответствуют малые значения углов отклонения ветра от градиентного.

Изменение вектора ветра с высотой в пограничном слое атмосферы в северном полушарии, вычисленное по формуле (13, 29), представлено на рис. 117. На этом рисунке по оси абсцисс отложены составляющие скорости ветра вдоль изобар, а по оси ординат — составляющие скорости ветра, перпендикулярные к изобарам.

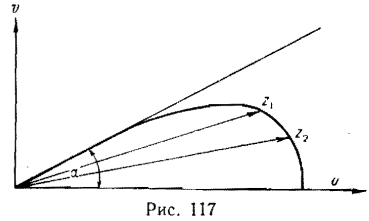
Стрелками показано изменение направления ветра относительно геострофического. Из рисунка видно, что с удалением от земной поверхности ветер поворачивает вправо и усиливается до совпадения с градиентным на верхней границе пограничного слоя атмосферы. В южном полушарии вращение ветра с высотой в пограничном слое атмосферы происходит влево. Поскольку зимой над морем турбулентность больше, чем летом, то и отклонение ветра от градиентного зимой больше, чем летом. Над континентом наблюдается обратное соотношение.

Суточный ход ветра. С воздействием сил трения связаны суточные и годовые колебания ветра. В пограничном слое атмосферы суточный ход скорости и направления ветра над сушей выражен довольно отчетливо и зависит от суточного хода турбулентного обмена. Наиболее ясно он выражен при устойчивой хорошей погоде.

В дневное время с усилением турбулентного обмена скорость ветра в слое от 0 до 100—150 м возрастает, а выше (от 100—150 м до 1000—1500 м) убывает по сравнению со скоростью ветра в ночное время. Эти изменения в суточном ходе ветра в средних широтах составляют 3—5 м/сек. Угол отклонения ветра в нижнем слое меньше днем, чем ночью, а в верхнем — наоборот.

Такой ход ветра в течение суток над сушей объясняется следующим. К ночи с прекращением конвекции и уменьшением турбулентного обмена в нижнем слое скорость ветра быстро уменьшается, а в верхнем ввиду ослабления тормозящего влияния нижних слоев скорость ветра ночью возрастает до своего максимального значения, определяемого величиной барического градиента на соответствующем уровне.

Будучи связан с ходом температуры, суточный ход скорости ветра летом больше, чем зимой; он больше в ясные дни, чем в пасмурные. Над океанами суточный ход ветра почти незаметен.

Годовой ход ветра определяется как климатическими особенностями района, так и местными условиями. В умеренной зоне северного полушария наибольшие скорости наблюдаются зимой, наименьшие — летом, что объясняется изменением горизонтальных градиентов температуры от зимы к лету (зимой они больше). Внутри континентов, где зимой находятся стационарные антициклоны, скорость ветра, наоборот, зимой меньше, а летом больше.

Сведения об авторах и источниках:

Автор: Н. И. Егоров, И. М. Безуглый, В. А. Мнежинский, и др.

Источник: Морская гидрометеорология

Данные публикации будут полезны для курсантав морских учебных заведений и капитанаов/штурманов гражданского флота, интересующимся глубоким пониманием гидрометеорологии