Барический градиент и силы ветра: физика атмосферы

Барический градиент. Из гидродинамики известно, что барический градиент есть сила, действующая на единицу объема, равная

где р — плотность;
n — направление нормали к изобарической поверхности;
U — вектор скорости ветра.

В метеорологии принято рассчитывать барический градиент, действующий на единицу массы

Составляющие этой силы на координатные оси будут

Оценка величин показывает, что горизонтальные составляющие ускорений барического градиента на два порядка выше вертикальных, несмотря на то, что горизонтальные составляющие градиента давления на 4—5 порядков меньше вертикальных. Вертикальные составляющие барического градиента уравновешиваются силой тяжести, поэтому мы можем записать

Следовательно, третье уравнение последней системы сводится к основному уравнению статики

Отсюда мы заключаем, что основной причиной атмосферного движения является горизонтальная составляющая барического градиента, которая всегда направлена в сторону убывания давления. Если бы на движущийся воздух действовала только эта сила, то направление ветра совпадало бы с ее направлением.

Сила Кориолиса. При вращении Земли восточная часть горизонта все время опускается, а западная — поднимается; в результате этого вертикальная составляющая силы Кориолиса обусловливает отклонение вверх тел, движущихся к востоку, и вниз — движущихся к западу. Вертикальная составляющая силы Кориолиса накладывается на силу тяжести, несколько увеличивая или уменьшая ее. Горизонтальная составляющая силы Кориолиса, обусловленная вращением плоскости горизонта, вызывает в северном полушарии отклонение тел вправо от направления их движения, а в южном — влево.

В метеорологии существенное значение имеет лишь горизонтальная составляющая силы Кориолиса, так как ее вертикальная составляющая лишь несколько изменяет силу тяжести; формула для горизонтальной составляющей имеет вид:

Сила Кориолиса не оказывает влияния на скорость движения частицы, а лишь изменяет направление ее движения. Эта сила оказывает влияние на движение всех тел на земной поверхности, в атмосфере и гидросфере.

Сила трения. В связи с тем, что между молекулами газа действуют силы молекулярной вязкости, при движении воздуха образуется особая сила — сила трения. Физический смысл этой силы элементарно можно представить себе следующим образом.

Непосредственно на поверхности Земли в слое, измеряемом миллиметрами, из-за торможения потока подстилающей поверхностью скорость ветра всегда равна нулю. Однако это не значит, что молекулярного обмена между этим спокойным слоем и вышележащими не существует. Вследствие теплового движения молекул, последние проникают и в движущиеся слои, а из движущихся — в неподвижный.

Естественно, что молекулы движущихся слоев обладают большим количеством движения, чем молекулы неподвижных слоев, поэтому обмен молекулами между этими слоями приводит к тому, что от поверхности Земли до некоторой высоты скорость ветра возрастает более или менее равномерно.

Изменение количества движения, изложенное выше, можно рассматривать как результат действия некоторой силы — силы трения. Эта сила выражается следующей формулой:

При неравномерном изменении ветра по высоте при определенных условиях возникают завихрения и развивается турбулентность. С развитием турбулентности, коэффициент которой намного больше коэффициента молекулярной вязкости, в обмене количеством движения уже участвуют объемы, намного превышающие размеры молекул. Это приводит к тому, что влияние сил трения распространяется на высоты до 1—2 км.

Поскольку на развитие турбулентности большое влияние оказывает шероховатость поверхности, скорость потока и степень устойчивости стратификации атмосферы, слой трения в разных условиях имеет различную высоту.

По аналогии с силами молекулярного трения можно записать и силы турбулентного трения τ_t в виде

где А — коэффициент турбулентного обмена.

В этом случае под вектором скорости потока уже понимают некоторое его среднее значение (по времени или по пространству), так как истинная скорость из-за турбулентности будет испытывать мгновенные колебания.

Известно, что при движении твердого тела в жидкости сила трения прямо пропорциональна плотности жидкости и скорости потока и направлена в сторону, противоположную движению. Таким образом, здесь сила трения приводит только к уменьшению скорости движения. В случае движения воздуха дело обстоит сложнее. Поскольку , вышележащие слои отличаются от нижележащих по направлению и скорости потока вследствие обмена количеством движения, то между направлением движения воздуха и силой трения образуется угол около 15—30°.

Центробежная сила. В том случае, когда изобары имеют круговую форму (циклоны или антициклоны), ко всем рассмотренным силам добавляется центробежная сила Е. Отнесенная к единице массы она равна

Уравнения движения в атмосфере. Теперь запишем уравнение движения в атмосфере. В векторной форме оно имеет следующий вид:

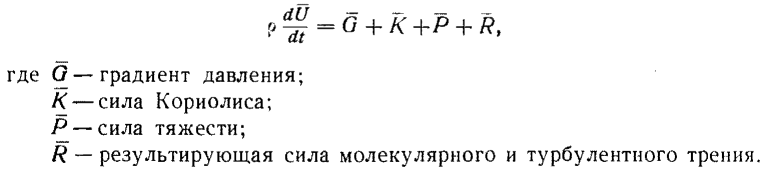
В координатной форме это уравнение в метеорологии используется в следующем виде:

где U_x и U_y составляющие скоростей ветра пo осям X и Y; вертикальной составляющей U_z обычно пренебрегают.

Решение уравнений (13, 18) в общем виде представляет большие трудности главным образом из-за того, что составляющие скоростей по осям являются неизвестными функциями высоты U_x(z), U_y(z), U_z(z), а также вследствие того, что коэффициент турбулентного обмена А, или коэффициент турбулентности k = A/p, является переменным, т. е. сложной функцией пространства и времени. В связи с этим уравнения движения в метеорологии решаются с различными степенями приближения. Наиболее часто они решаются в предположении стационарности движения

Тогда, задаваясь различными теоретическими моделями для к, находят решения для скорости потока. Простейшими случаями являются модели градиентного и геострофического ветра, к рассмотрению которых мы и перейдем.

Если при установившемся движении пренебречь силой трения, то на движущийся воздух будут действовать только три силы: барический градиент, сила Кориолиса и центробежная сила.

Установившийся ветер, не зависящий от трения, называется градиентным ветром. Частным его случаем, когда движение прямолинейно, является геострофический ветер. Поскольку влияние трения наиболее сильно проявляется в пограничном слое, то в свободной атмосфере истинный ветер близок к градиентному.

Сведения об авторах и источниках:

Автор: Н. И. Егоров, И. М. Безуглый, В. А. Мнежинский, и др.

Источник: Морская гидрометеорология

Данные публикации будут полезны для курсантав морских учебных заведений и капитанаов/штурманов гражданского флота, интересующимся глубоким пониманием гидрометеорологии