ГЛАВА 6. ДИСПЕРСИЯ И ПОГЛОЩЕНИЕ СВЕТА
Дисперсия света
1. Дисперсия света (от лат. dispersio - рассеивание) - это зависимость показателя преломления вещества от длины волны света. Первым изучать дисперсию стал Ньютон в 1666 году. Пропустив узкий пучок солнечного света, входящий через отверстие в ставне, через трехгранную стеклянную призму, он получил на экране удлиненное окрашенное пятно, которое назвал спектр (от лат. spectrum - система элементов) (рис.179).
 Ньютон объяснил появление спектра тем, что лучи разного цвета по – разному преломляются. В результате пучок белого света расщепляется с помощью призмы на семь отдельных цветов - красный, оранжевый, желтый, голубой, синий, фиолетовый. Более всего отклоняются фиолетовые лучи, менее всего - красные.
Ньютон объяснил появление спектра тем, что лучи разного цвета по – разному преломляются. В результате пучок белого света расщепляется с помощью призмы на семь отдельных цветов - красный, оранжевый, желтый, голубой, синий, фиолетовый. Более всего отклоняются фиолетовые лучи, менее всего - красные.
Поскольку цвет луча определяется длиной волны l, а угол преломления луча на границе определяется показателем преломления по отношению к этому лучу, то дисперсия света сводится к зависимости показателя преломления среды n от длины волны света l, то есть n=n(l). В настоящее время понятие дисперсии применимо к любой физической величине, зависящей от l. Говорят, например, о дисперсии удельной оптической активности, о дисперсии постоянной магнитного вращения Верде, дисперсии постоянной Керра и др.
2. Дисперсионная способность разных веществ различна. То есть совершенно одинаковые призмы, изготовленные из разных веществ, дают спектр одного и того же пучка разной длины. Чем сильнее растянут спектр, тем выше считается дисперсионная способность. Мерой дисперсионной способности является коэффициент дисперсии или число Аббе n. n = (nD – 1)ç(nF – nC). Число Аббе (21.1)
Здесь nD - показатель преломления вещества для D - линии натрия (l = 589,3 нм), nF - то же для F - линии водорода (l = 486,1 нм), nC - то же для С - линии водорода (l = 656,3 нм). Чем больше дисперсионная способность вещества, тем меньше число Аббе.
| Таблица 21.1 | |||
| Название | Марка | 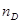
| n |
| Борсилик. крон | С – 20 | 1.5100 | 63.4 |
| Силикатный крон | С – 7 | 1.5147 | 60.6 |
| Крон | С – 12 | 1.5181 | 58.9 |
| Крон – Флинт | С – 49 | 1.5262 | 51.0 |
| Баритовый крон | С – 17 | 1.5399 | 59.7 |
| Легкий флинт | С – 16 | 1.5783 | 41.7 |
| Флинт | С – 8 | 1.6129 | 36.9 |
| Флинт | С – 3 | 1.6242 | 35.9 |
| Тяжелый флинт | С – 18 | 1.7550 | 27.5 |
 Как видно из таблицы 21.1, где приведены значения коэффициента дисперсии n оптических стекол, наибольшая дисперсия у тяжелых сортов стекол, для которых n »30. Сравнивать дисперсионную способность разных веществ удобно методом скрещенных призм Ньютона. Суть метода в том, что пучок света пропускается через две призмы, преломляющие ребра которых ориентированы перпендикулярно друг к другу (рис.180). Если дисперсии обеих призм одинаковы, то спектр вытягивается в прямую линию, если разные, то спектр искривляется. По характеру и величине искривления можно судить, какое вещество обладает большей дисперсией.
Как видно из таблицы 21.1, где приведены значения коэффициента дисперсии n оптических стекол, наибольшая дисперсия у тяжелых сортов стекол, для которых n »30. Сравнивать дисперсионную способность разных веществ удобно методом скрещенных призм Ньютона. Суть метода в том, что пучок света пропускается через две призмы, преломляющие ребра которых ориентированы перпендикулярно друг к другу (рис.180). Если дисперсии обеих призм одинаковы, то спектр вытягивается в прямую линию, если разные, то спектр искривляется. По характеру и величине искривления можно судить, какое вещество обладает большей дисперсией.
3. Формула Коши. Поскольку дисперсия отражает механизм взаимодействия света с веществом, то для ее объяснения помимо модели света нужна еще модель вещества. В 30 –х годах 19 века Огюстен Коши, опираясь на идеи Френеля о взаимодействии частиц упругого эфира с частицами вещества (молекулами), получил формулу, выражающую зависимость показателя преломления n от длины волны l:
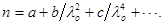 Формула Коши (21.2)
Формула Коши (21.2)
Здесь lо – длина волны в вакууме, а, b, с – постоянные, определяемые из опыта для каждого вещества. Формула Коши хорошо согласуется с экспериментом для ряда веществ.
4. Аномальная дисперсия. В 1862 году француз Ле Ру, наблюдая преломление белого света в призме, наполненной парами йода, установил, что синие лучи преломляются меньше, чем красные. Этот противоречащий дисперсии случай Ле Ру назвал аномальной дисперсией. После него обычную дисперсию, соответствующую формуле Коши, стали называть нормальной дисперсией.
При нормальной дисперсии показатель преломления вещества уменьшается с ростом длины волны, а при аномальной дисперсии – растет с увеличением длины волны.
 В 1870 – 71 г.г. немец Август Кундт пришел к выводу, что аномальная дисперсия присуща, по-видимому, всем веществам. Она представляет собой определенные участки кривой нормальной дисперсии. Кроме того оказалось, что в области аномальной дисперсии наблюдается сильное поглощение света веществом.
В 1870 – 71 г.г. немец Август Кундт пришел к выводу, что аномальная дисперсия присуща, по-видимому, всем веществам. Она представляет собой определенные участки кривой нормальной дисперсии. Кроме того оказалось, что в области аномальной дисперсии наблюдается сильное поглощение света веществом.
На рис.181-а показан спектр, полученный двумя скрещенными призмами из одинакового стекла. Этот спектр соответствует нормальной дисперсии, с уменьшением длины волны l показатель преломления n увеличивается.
На рис.181 б показан спектр, получающийся, когда одна из призм имеет участок аномальной дисперсии. Здесь та, что разворачивает спектр по вертикали. На сплошных участках ход дисперсии нормальный, но на краях разрыва наблюдается аномалия. Лучи, соответствующие точке М, имеют большую длину волны и отклоняются сильнее, чем лучи, соответствующие точке N, длина волны которых меньше.
У Ле Ру область поглощения занимала почти весь спектр. Он видел только красный и фиолетовый цвета. На нашем рисунке точка М уходит к концу Кр, а точка N – к концу Ф. Фиолетовый конец спектра у Ле Ру находился по нашему рисунку выше, чем красный.
Позднее выяснилось, что у многих веществ имеются несколько таких областей сильного поглощения и аномального хода дисперсии.
5. Электронная теория дисперсии Лоренца. К 1892 году Гендрик Лоренц сформулировал основные положения всеобщей электронной теории вещества. В ее рамках объяснялась большая группа явлений – теплопроводность, электропроводность, дисперсия, поглощение света и др. Основные положения электронной теории дисперсии состоят в следующем.
Свет есть электромагнитная волна, распространяющаяся в пространстве. Взаимодействующее со светом вещество моделируется системой квазиупругих резонаторов. То есть полагается, что каждый атом содержит один или несколько внешних электронов, способных испытывать вынужденные колебания под действием переменного электрического поля волны. Эти периферийные электроны называют оптическими.
Остальные электроны являются внутренними. Считается, что их взаимодействие с электрическим полем световой волны незначительно, и им можно пренебречь.
Лоренц предположил, что сила, удерживающая электрон в атоме, в пределах малых отклонений пропорциональна величине смещений электрона от положения равновесия. Рассмотрим вначале случай, когда вещество состоит из одинаковых атомов, каждый из которых имеет один оптический электрон.
а. Атомы вещества одинаковы и имеют по одному оптическому электрону. Полагаем, что на оптический электрон в электрическом поле световой волны действует три силы: квазиупругая сила 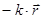 , диссипативная сила, подобная силе вязкого трения
, диссипативная сила, подобная силе вязкого трения 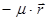 и вынуждающая сила со стороны электрического поля волны
и вынуждающая сила со стороны электрического поля волны 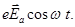
В проекции на радиус-вектор 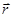 уравнение движения электрона принимает вид:
уравнение движения электрона принимает вид:
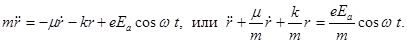 (21.3)
(21.3)
Это известный в механике случай вынужденных колебаний в системе с затуханием. Здесь m, e – масса и заряд электрона, r – смещение электрона от положения равновесия, 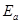 – амплитуда напряженности электрического поля световой волны, w – ее частота.
– амплитуда напряженности электрического поля световой волны, w – ее частота.
Конечно, никаких квазиупругих сил и вязкого трения в молекулах и атомах нет. Строгая теория дисперсии может быть построена лишь в рамках квантовой физики. В классической теории дисперсии параметры m, k – формально введенные коэффициенты. Однако классическая электронная теория позволяет построить достаточно простую модель диспергирующей среды. А результаты, полученные в рамках такой классической модели, совпадают с результатами квантовой теории.
Вынужденные колебания электрона в системе с затуханием есть сумма затухающих собственных колебаний электрона и вынужденных. Резонно допустить, что время затухания t внутриатомных колебаний очень мало. Тогда спустя время t, оптический электрон будет совершать только вынужденные колебания по закону: 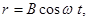 где (21.4)
где (21.4)
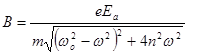 – амплитуда вынужденных колебаний. (21.5)
– амплитуда вынужденных колебаний. (21.5)
Здесь 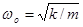 – частота собственных колебаний электрона,
– частота собственных колебаний электрона, 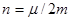 . Упростим задачу. Допустим, что затухания нет, n = 0, а собственные колебания электрона пренебрежимо малы. Тогда амплитуда вынужденных колебаний:
. Упростим задачу. Допустим, что затухания нет, n = 0, а собственные колебания электрона пренебрежимо малы. Тогда амплитуда вынужденных колебаний: 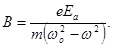 (21.6)
(21.6)
Найдем связь показателя преломления n с частотой света w. Под влиянием электрического поля световой волны все оптические электроны синхронно смещаются. В результате каждый атом превращается в диполь с электрическим моментом p = er.
 Если в единице объема среды N атомов, то электрический момент единичного объема (вектор поляризации) равен:
Если в единице объема среды N атомов, то электрический момент единичного объема (вектор поляризации) равен: 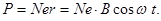 (21.7)
(21.7)
Так как 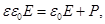 (22.8)
(22.8)
то, выразив отсюда e = n2 и подставив P из формулы (21.7), получаем: 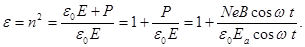 (21.9)
(21.9)
Сократив дробь на 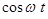 и подставив B из формулы (21.6), получаем зависимость показателя преломления вещества n от частоты света w.
и подставив B из формулы (21.6), получаем зависимость показателя преломления вещества n от частоты света w. 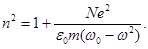 (21.10)
(21.10)
На рисунке 182 видно, что в области частот w < w0 показатель преломления n > 1 и растет с увеличением частоты света w (нормальная дисперсия). В области частот w > w0 n <1 и тоже растет с увеличением частоты света w (нормальная дисперсия).
При w ® w0 происходит резонансное поглощение света, 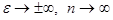 . Обращение e и n в бесконечность не имеет физического смысла и получилось в результате упрощенного предположения об отсутствии затухания в атомных резонаторах. В этих условиях амплитуда вынужденных колебаний резонаторов должна неограниченно возрастать, а резонаторы – разрушаться.
. Обращение e и n в бесконечность не имеет физического смысла и получилось в результате упрощенного предположения об отсутствии затухания в атомных резонаторах. В этих условиях амплитуда вынужденных колебаний резонаторов должна неограниченно возрастать, а резонаторы – разрушаться.
В реальных опытах не наблюдается столь катастрофических изменений. Следовательно, резонаторы диссипативны. Благодаря рассеянию энергии резонаторов амплитуда их вынужденных колебаний ограничена, поэтому кривая зависимости n = n(w) не имеет разрыва (рис.183).
 Области аномальной дисперсии соответствует участок кривой MN, проходящий через резонансную частоту wо. Кривая х - зависимость поглощения света от частоты w.
Области аномальной дисперсии соответствует участок кривой MN, проходящий через резонансную частоту wо. Кривая х - зависимость поглощения света от частоты w.
б. Атомы вещества различны и имеют по несколько оптических электронов. Формула (21.9) усложняется, поскольку поляризация вещества будет определяться суммой вкладов в поляризацию каждой группы резонаторов. Вещество должно иметь в этом случае столько собственных частот колебаний резонаторов w 01, w 02 ,…, сколько в нем типов оптических электронов.
 Опыт показал, что большинство веществ действительно имеют по несколько участков аномальной дисперсии, соответствующих определенным резонансным частотам w 01, w 02… . Все частоты отчетливо подразделяются на две группы. Одна группа находится в инфракрасной области спектра, другая – в видимой и ультрафиолетовой (рис.184).
Опыт показал, что большинство веществ действительно имеют по несколько участков аномальной дисперсии, соответствующих определенным резонансным частотам w 01, w 02… . Все частоты отчетливо подразделяются на две группы. Одна группа находится в инфракрасной области спектра, другая – в видимой и ультрафиолетовой (рис.184).
Сделанные по значениям резонансных частот оценки удельного заряда колеблющихся частиц показали, что поглощение в видимой и УФ области обусловлено оптическими электронами, а в ИК области – ионами.
6. Удельная рефракция. Приведенные в предыдущем пункте рассуждения относятся к изолированным атомам, электрические поля которых не возмущают друг друга. Поэтому лучше всего они применимы к газам. В конденсированных средах электрические поля атомов существенно влияют друг на друга. Поэтому действующее на резонатор поле представляет собой сумму двух полей – световой волны и поляризованных молекул. Решение уравнения вынужденных колебаний резонаторов с учетом этих эффектов приводит к выявлению важной оптической характеристики вещества, слабо зависящей от его агрегатного состояния. 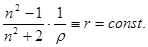 Формула Лоренц – Лоренца (21.11)
Формула Лоренц – Лоренца (21.11)
Величину r называют удельной рефракцией вещества, r – плотность вещества. Формулу (21.11) получили в 1880 году независимо Гендрик Лоренц и датский физик Людвиг Лоренц.
Для многих веществ эта формула очень хорошо подтверждается экспериментом. Например, для воды и кислорода при переходе из газообразного в жидкое состояние, когда плотность r увеличивается на три порядка, удельная рефракция r изменяется лишь на 2 – 3%.
Дата добавления: 2020-05-20; просмотров: 606;