Теорема 3 (следствие из формулы Грина).
Если в односвязной области  определены непрерывные функции
определены непрерывные функции  ;
;  с непрерывными частными производными, и точки
с непрерывными частными производными, и точки  , то интеграл не зависит от формы пути интегрирования тогда и только тогда, когда
, то интеграл не зависит от формы пути интегрирования тогда и только тогда, когда

Пример:
Показать, что интеграл J не зависит от формы пути и вычислить его (рис. 7.9)



 , т.е. выполнены условия теоремы 3.
, т.е. выполнены условия теоремы 3.

(на пути AC  ; на пути CB
; на пути CB  )
)

Рис. 7.9
7.4. Приложение криволинейных интегралов
С помощью криволинейных интегралов I-го рода можно вычислять координаты центра масс материальной линии 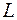 с переменной плотностью
с переменной плотностью  по формулам.
по формулам.

Здесь  – масса.
– масса.
Криволинейный интеграл I рода вида
 , где
, где  – расстояние точки
– расстояние точки  до некоторой оси, а
до некоторой оси, а  – плотность в точке M, задает так называемый момент инерции материальной линии
– плотность в точке M, задает так называемый момент инерции материальной линии 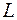 относительно некоторой оси.
относительно некоторой оси.
Момент инерции относительно начала координат также можно вычислить с помощью криволинейного интеграла I рода:

Здесь выражение  задает расстояние от точки
задает расстояние от точки  до начала координат.
до начала координат.
Как уже говорилось, с помощью криволинейного интеграла по координатам вычисляется работа A переменной силы  на пути
на пути 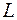 :
:
 , где – вектор-функция, определяющая кривую
, где – вектор-функция, определяющая кривую 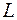 .
.
Если кривая – замкнутая, то такая работа называется циркуляцией:
 .
.
7. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
8.1. Вычисление площади поверхности

Рис. 8.1
Рассмотрим поверхность  (см. рис. 8.1).
(см. рис. 8.1).
 : а) однозначна;
: а) однозначна;
б)  обладает непрерывной частной производной;
обладает непрерывной частной производной;
в) проектируется в область  .
.
Задача: Найти площадь поверхности  –
– 
Разобьем о.о.ф.  , область
, область  , на куски
, на куски  ; тогда на
; тогда на  получим соответствующее разбиение
получим соответствующее разбиение 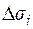 .
.

Рис. 8.2
В каждой  произвольно выберем
произвольно выберем  и
и  . В каждой точке
. В каждой точке  проведем касательную плоскость (см. рис. 8.2). Найдем площадь того куска касательной плоскости, который проектируется (вместе с
проведем касательную плоскость (см. рис. 8.2). Найдем площадь того куска касательной плоскости, который проектируется (вместе с 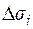 ) в
) в  . Уравнение касательной плоскости в точке
. Уравнение касательной плоскости в точке  имеет вид:
имеет вид:

А вектор  – вектор нормали к поверхности в точке
– вектор нормали к поверхности в точке  . Через
. Через  обозначим угол между касательной плоскостью и плоскостью
обозначим угол между касательной плоскостью и плоскостью  . Он равен углу между
. Он равен углу между  и единичным вектором
и единичным вектором  оси
оси  . Тогда
. Тогда 
Площадь куска касательной плоскости примерно равна площади куска поверхности 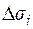 , который проектируется в
, который проектируется в  . Тогда
. Тогда
 .
.
Это равенство следует из прямоугольного треугольника (см. рис. 8.3).

Рис. 8.3
Составим интегральную сумму:
 .
.
Обозначим  ,
,
где  – элемент поверхности
– элемент поверхности  , при условии, что предел существует и не зависит от разбиения.
, при условии, что предел существует и не зависит от разбиения.

Рис. 8.4
Пример:
Вывести формулу для вычисления площади поверхности сферы радиуса R.
Поверхность сферы задается уравнением  . Отсюда уравнение верхней полусферы
. Отсюда уравнение верхней полусферы  , проекцией полусферы на
, проекцией полусферы на  является область
является область  , представляющая собой круг:
, представляющая собой круг:  (см. рис. 8.4).
(см. рис. 8.4).





8.2. Поверхностные интегралы I-го рода
8.2.1. Определение поверхностного интеграла I-го рода.
Мерой фигуры  (поверхности в пространстве) назовем ее площадь
(поверхности в пространстве) назовем ее площадь  .Поверхность будем предполагать гладкой, т.е. такой, что в любой ее точке существует касательная плоскость к поверхности. На поверхности
.Поверхность будем предполагать гладкой, т.е. такой, что в любой ее точке существует касательная плоскость к поверхности. На поверхности  зададим функцию
зададим функцию  , определенную в каждой точке
, определенную в каждой точке  . Разобьем
. Разобьем  на произвольные части
на произвольные части  , на каждом из кусков поверхности
, на каждом из кусков поверхности  произвольно выберем точку
произвольно выберем точку  , вычислим значение функции в этих точках
, вычислим значение функции в этих точках  и составим интегральную сумму следующего вида:
и составим интегральную сумму следующего вида:  .
.
Обозначим  . Тогда предел, при условии, что он существует и не зависит от разбиения, равный
. Тогда предел, при условии, что он существует и не зависит от разбиения, равный
 – называется поверхностным интегралом от функции
– называется поверхностным интегралом от функции  по площади поверхности
по площади поверхности  или поверхностным интегралом I-го рода, где
или поверхностным интегралом I-го рода, где  – элемент поверхности.
– элемент поверхности.
Поверхностный интеграл I-го рода является частным случаем интеграла по фигуре. Следовательно, для него верны свойства: линейность, аддитивность, теорема об оценке, теорема о среднем, при  равен
равен  .
.
8.2.2. Вычисление поверхностного интеграла.
Пусть гладкая поверхность  однозначно проектируется на какую-либо координатную плоскость. Например, пусть
однозначно проектируется на какую-либо координатную плоскость. Например, пусть  задана уравнением
задана уравнением  и проектируется в область
и проектируется в область  плоскости
плоскости  . Элемент поверхности
. Элемент поверхности  проектируется на площадку
проектируется на площадку  области
области  , и если
, и если  – угол между осью Oz и нормалью к
– угол между осью Oz и нормалью к  , то
, то
 и
и

Пример:


Рис. 8.5
Вычислить  , где
, где  – поверхность треугольника, образованного пересечением плоскости
– поверхность треугольника, образованного пересечением плоскости 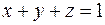 с координатными плоскостями (см. рис. 8.5).
с координатными плоскостями (см. рис. 8.5).

Пример:
Вычислить площадь части поверхности  , заключенную внутри цилиндрической поверхности Ц (см. рис. 8.6).
, заключенную внутри цилиндрической поверхности Ц (см. рис. 8.6).


Рис. 8.6

 – уравнение направляющей цилиндра.
– уравнение направляющей цилиндра.

8. СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ПОЛЯ
9.1. Скалярные поля. Основные понятия.
Определение скалярного поля.
В области 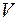 пространства задано скалярное поле, если любой точке
пространства задано скалярное поле, если любой точке  поставлен в соответствие скаляр
поставлен в соответствие скаляр 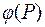

В декартовой системе координат задание скалярного поля 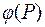 соответствует заданию в области
соответствует заданию в области 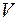 функции трех переменных
функции трех переменных 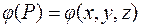 .
.

Примеры скалярных полей:
Поле температур  , поле освещенности
, поле освещенности  , поле электрических зарядов
, поле электрических зарядов  , поле плотности распределения масс
, поле плотности распределения масс  .
.
Будем предполагать, что 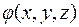 – непрерывная, с непрерывными частными производными.
– непрерывная, с непрерывными частными производными.
Поверхностью уровня скалярного поля 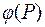 называется геометрическое место точек, в которых значение поля равны одной и той же постоянной величине
называется геометрическое место точек, в которых значение поля равны одной и той же постоянной величине 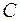 , т.е.
, т.е.

Примеры:
Найти поверхности уровня скалярных полей
1) 
 – концентрические сферы
– концентрические сферы
2)  ;
;
 – гиперболический цилиндр
– гиперболический цилиндр
Эти поверхности изображены на рисунке 9.1.


Рис. 9.1
Дата добавления: 2020-03-21; просмотров: 388;