Уравнение прямой с угловым коэффициентом.
Прямая на плоскости и её уравнения. Угол между двумя прямыми. Взаимное положение прямых на плоскости.
1) Уравнение прямой на плоскости.
Уравнением линии на плоскости называется уравнение относительно переменных (x,y), которому удовлетворяют координаты любой точки линии и только они.
Общий вид уравнения линии в декартовой системе координат: 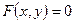 .
.
Это уравнение определяет линию как некоторое геометрическое место точек, т.е. совокупность точек, обладающих некоторым свойством, исключительно им присущим.
Чтобы составить уравнение линии как некоторого геометрического места точек, необходимо:
a. взять произвольную точку с текущими координатами x и у;
b. записать общее свойство точек данного геометрического места в виде тождества;
c. преобразовать полученное тождество в уравнение.
Точки пересечения двух линий 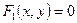 и
и 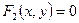 находят из системы уравнений
находят из системы уравнений 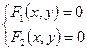 . Если система совместна, то линии пересекаются. Число точек пересечения равно числу решений системы.
. Если система совместна, то линии пересекаются. Число точек пересечения равно числу решений системы.
2) Прямая на плоскости.
Уравнение прямой с угловым коэффициентом.
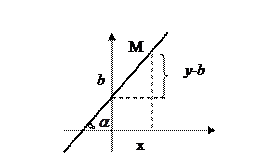
Дано: т. 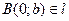
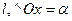
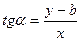
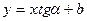 ,
, 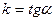 ,
, 
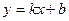 /
/
Дата добавления: 2020-02-05; просмотров: 383;