Преобразования Лоренца и 4-пространство (мир Минковского).

Если система декартовых координат 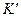с текущим временем 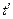движется относительно декартовой системы координат 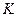с текущим временем 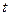с постоянной скоростью 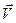, причём часы в обеих системах координат синхронизированы тем условием, что в начальные моменты времени начала координат обеих систем совпадали, преобразования Лоренца имеют вид:

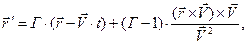
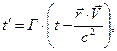
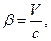
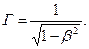(1)

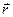Здесь и 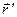- радиус-вектор точки наблюдения в системе координат 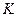и радиус-вектор той же точки наблюдения в системе 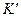. Но произвольные декартовы системы координат всегда можно ориентировать (т.е. преобразовать) так, чтобы скорость относительного движения систем 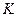и 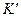была направлена вдоль координаты 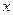и 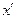, а остальные координатные направления совпадали (для простоты мы рассматриваем «правые» координатные системы). В этом случае преобразования Лоренца значительно упрощаются:

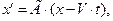
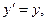
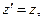
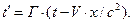(2)

Интервал между событиями с «координатами» {x₁,y_1,z₁,t₁} и {x₂,y_2,z₂,t₂} в пространстве-времени (мир Минковского) по определению равен

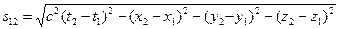. (3)

Для двух событий, происходящих в бесконечно близких точках пространства через бесконечно малый промежуток времени, квадрат этого выражения приобретает форму:

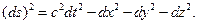(4)

Напомним, что интервал (3) между двумя «близкими» событиями в СТО является инвариантом по отношению к преобразованиям Лоренца. В этом смысле он подобен расстоянию между двумя близкими точками трёхмерного евклидова пространства, которое тоже является инвариантным относительно преобразований поворота и сдвига декартовых систем координат:

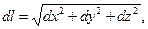(5)

с его помощью определяется метрика евклидова пространства. Сравнивая между собой выражения (4) и (5), убеждаемся, что метрические свойства пространства-времени Г. Минковского и трехмерного евклидова пространства существенно различны и это различие проявляется не только в увеличении размерности пространства.

В СТО можно использовать симметричные обозначения основных переменных:

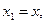
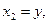
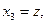
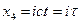(6)

для «мнимого времени» и

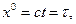
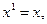
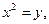
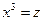(7)

для «действительного времени». В общей теории относительности использование координат (7) предпочтительнее, а при изложении закономерностей электродинамики удобнее использование координат (6): как это увидим ниже, в этом представлении можно не делать разницы между контра- и ковариантными величинами.

Квадрат интервала между близкими событиями (4) при использовании набора координат (6) четырёхмерного пространства можно использовать в виде:

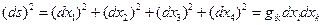, (8)

где в объекте 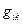отличны от нуля элементы 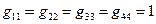. Поскольку матрица, обратная по отношению к единичной, совпадает с исходной, ковариантные и контравариантные величины в системе координат (6) совпадают друг с другом. Это очень удобно при рассмотрении законов электродинамики.

Аналогичное выражение для квадрата интервала между близкими событиями в представлении (7) имеет вид

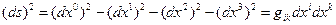, (9)

где в объекте 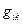отличны от нуля элементы .

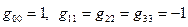Квадрат модуля 4-вектора определяется либо по схеме (8), либо по схеме (9):

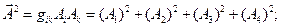(10)

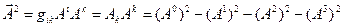. (11)

Преобразования Лоренца (2) с использованием симметричных координат тоже принимают различную форму, а компоненты 4-векторов преобразуются при переходе из системы координат К в систему координат К^/ по закону:

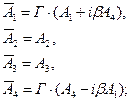(a) 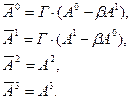(б) (12) Матрицы преобразования Лоренца для случая а) и для случая б) имеют вид

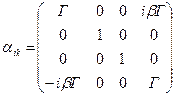, a) 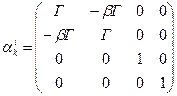б) (13)

Матрицы обратного преобразования Лоренца – это матрицы, обратные по отношению к исходным, они могут быть получены просто изменением знака параметра 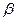. Заметим, что матрица с элементами смешанного строения описывает преобразование Лоренца контравариантных величин (набор координат (7) и соответствующее представление векторов и тензоров), для ковариантных составляющих вектора необходимо пользоваться обратной матрицей 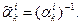В представлении а) – набор координат (6) - всё значительно проще: матрица обратного преобразования Лоренца является матрицей, транспонированной относительно исходной.

Целесообразность такого подробного анализа геометрических свойств 4-пространства Минковского и различия между контра- и ковариантными объектами при преобразованиях Лоренца обусловлена тем, что любое преобразование Лоренца с параметром 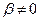исходные взаимно перпендикулярные координатные направления 4-пространства превращает в косоугольные, вынуждая нас задумываться, с какими объектами мы будем работать. Проще всего в электродинамике работать с набором координат (6).