Преобразования координат.

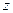Правилапреобразования контравариантных и ковариантных координат можно уяснить,рассматривая поворот против часовой стрелки исходной косоугольной двумерной (плоской) системы координат на заданный угол околоначала координат вокруг оси , перпендикулярной этой плоскости. Ниже нам понадобится аналогичное правило преобразования декартовых координат точки А, расположенной в плоскости 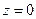. Рассмотрим рисунок 1.

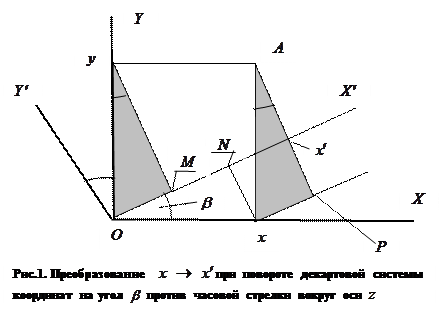
В исходной (опорной, условно «старой») системе декартовых координат 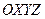положение точки А определено координатами 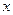, 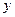и координатой 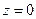. Эти координаты описывают соответствующие проекци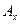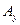и , и 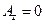радиус-вектора 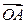. Преобразованная система декартовых координат 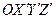( 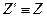), будем называть её «новой», повёрнута на заданный угол 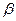околоначала координат вокруг оси 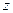. По построению отрезок 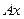является перпендикуляром к направлению 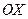, а отрезок 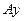- перпендикуляром к направлению 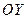. Из точки (x,0) плоскости z=0 проведём прямую линию, параллельную координатному направлению 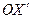. Отрезок 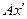и его продолжение – отрезок 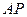- перпендикулярны и координатному направлению 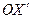, и прямой линии хР. Построим отрезок 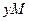, параллельный отрезку 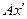и перпендикулярный координатному направлению 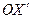. Таким же образом построим отрезок 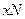. Пометим дугами равные между собой углы 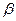. На этом построение можно считать законченным.

Рассматривая построенный рисунок, замечаем, что координата 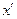определяется величиной отрезка 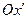: 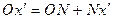. Величина отрезка 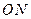равна проекции отрезка 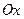на координатное направление 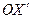: 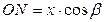. По построению отрезок 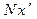равен отрезку 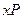. Треугольник 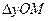, очевидно, равен треугольнику 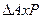, поэтому отрезок 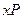равен отрезку 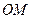. Длина отрезка 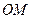определяется координатой у и величиной угла 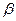: 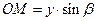. В итоге оказывается справедливым зависимость:

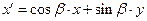. (1)

Рассмотрим проекцию радиус-вектора 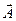на координатное направление 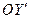(рисунок 2). Взаимная ориентация «старой» и «новой» декартовых систем координат на рис.2 полностью соответствует ориентации этих систем координат на рисунке 1. Из точки А опустим перпендикуляр на координатное направление 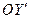и получим положение точки 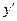. Из точки х опустим перпендикуляр на координатное направление 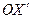и получим положение точки 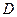. Из точки 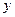проведём отрезок ,

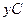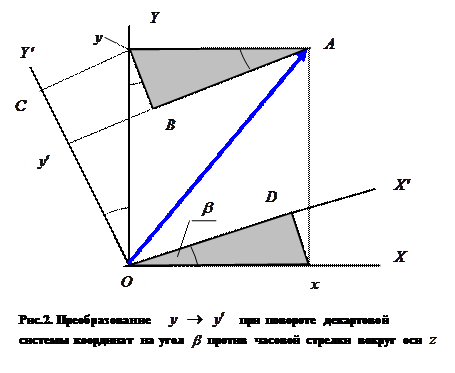
параллельный координатному направлению 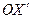и перпендикулярный координатному направлению 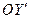. Из той же точки 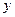опустим перпендикуляр на отрезок 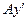и получим положение точки В. Так же как на рисунке 1, дугами пометим равные между собой углы 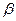. Треугольник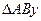и и 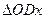, очевидно, равны друг другу. В этом случае длина отрезка 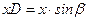равна длине отрезка 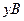. По построению отрезок 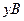равен отрезку 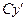. Из рисунка 2 следует: 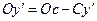. В силу этого справедлива зависимость:

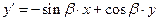. (2)

Учитывая очевидное для рассматриваемого случая соотношение

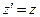, (3)

зависимости (1)-(3) запишем в векторно-матричной форме:

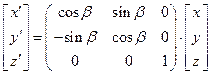. (4)

В символической форме записи соотношения (4) приобретают компактный вид:

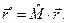(5)

В координатной форме записи имеем:

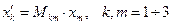. (6)

В соотношениях (5)-(6) 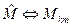- матрица «прямого» преобразования декартовых

координат 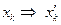в соответствии с зависимостью (6). Но зависимость (6) можно рассматривать и как систему линейных алгебраических уравнений для определения величин 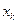по величинам 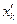, рассматриваемым как известные величины:

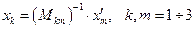. (7)

В зависимости (7) («обратное» преобразование декартовых координат) матрица 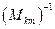является обратной матрицей по отношению к исходной матрице 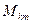. Для рассматриваемого случая имеем:

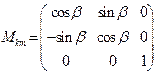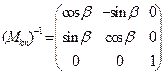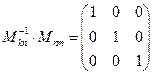, , , (8)

в общем случае матрица обратного преобразования декартовых координат является обратной матрицей (она совпадает с транспонированной) матрицей по отношению к матрице прямого преобразования

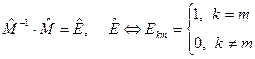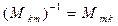, . (9)

Заметим также, что определитель матрицы 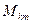равен единице, из правой координатной системы выполнялось преобразование в правую систему координат.

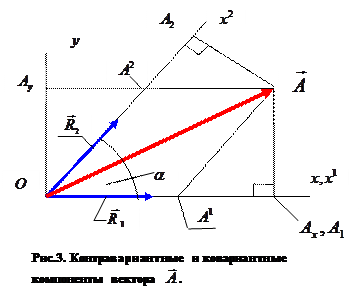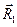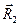Рассмотрим косоугольную систему координат (рис.3), координатные направления которой (контравариантный базис) заданы безразмерными ортами (единичными векторами) и , орт 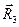совпадает с направлением оси z исходной системы декартовых координат (на рисунке не показан). Пусть направляющий вектор 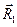исходной косоугольной системы координат совпадает по направлению с осью 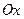исходной декартовой системы координат, пусть направляющий вектор 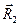исходной косоугольной системы координат составляет угол 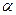с направлением оси 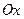исходной декартовой системы координат, а направляющий вектор 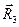исходной косоугольной системы координат направлен по оси z исходной декартовой системы координат. Проекции рассматриваемых направляющих векторов на оси координат исходной декартовой системы координат

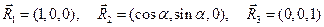(10)

позволяют вычислить направляющие векторы взаимной системы координат (ковариантный базис)

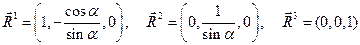(11)

и ковариантный и контравариантный метрические тензоры исходной косоугольной системы координат

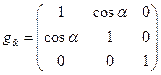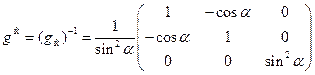, (12)

в соответствии с соотношениями разделов 13.1.3 и 13.1.4.

Контравариантные компоненты вектора 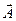, определённые выше зависимостями 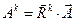(скалярное произведение), имеют вид:

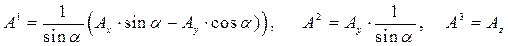. (13)

В векторно-матричной форме записи эти зависимости таковы:

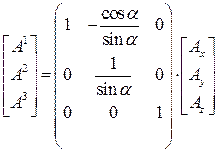. (14)

Соотношениями (14) определена матрица 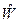преобразования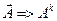

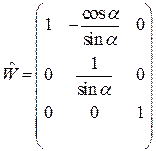, (15)

эта матрица не является особенной, что позволяет вычислить обратную матрицу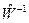

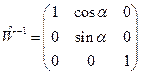. (16)

Используя полученный результат, можно записать совокупность зависимостей:

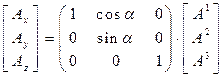. (17)

До сих пор мы делали формальные алгебраические выкладки. Обратимся к рисунку 3 и увидим, что показанные на нём контравариантные компоненты вектора 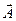и его декартовы проекции действительно подчиняются зависимостям (14).

Ковариантные компоненты вектора 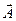определены соотношениями 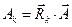, с учётом соотношений (10) это позволяет получить конкретные зависимости для рассматриваемого случая:

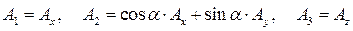. (18)

Запишем соотношения (17) в векторно-матричной форме:

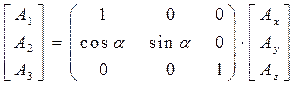. (19)

Соотношениями (19) определена неособенная матрица 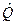преобразования :

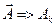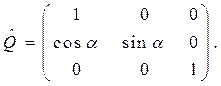
Её обратная матрица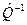

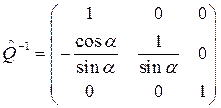(20)

позволяет восстановить величины проекций вектора 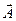на оси исходной декартовой системы координат по известным ковариантным координатам вектора :

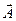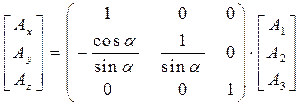. (21)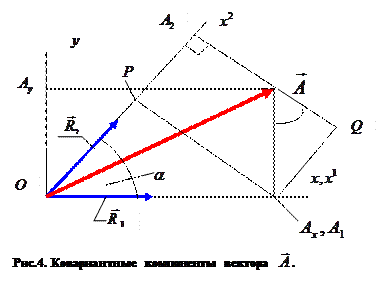

Выяснение геометрического смысла ковариантных компонент вектора 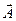и проверку правильности проведённых вычислений можно провести с помощью рис.4. На этом рисунке отрезок 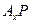по построению является перпендикуляром к координатному направлению 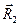, отрезок 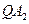параллелен отрезку 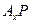, а отрезок 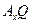перпендикулярен отрезку 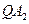. Легко видеть, что 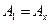, 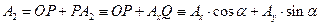. В результате мы убеждаемся в справедливости соотношений (19).

Матрицы 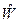и 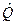функционально связаны между собой:

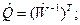
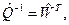
где индексом Т отмечена операция транспонирования.

Интересно отметить, что левые части соотношений (17) и (21) тождественно равны друг другу, значит, равны и их правые части. Приравнивая правые части соотношений (17) и (21), получаем новое соотношение, которое можно рассматривать либо как уравнение для определения ковариантных компонент вектора по его контравариантным компонентам, либо как уравнение для определения контравариантных компонент вектора по его ковариантным компонентам. Результаты решения этих уравнений, естественно, совпадают с результатами операций опускания или поднимания индекса с помощью соответствующего метрического тензора.

Рассмотрим «новую» косоугольную систему координат, полученную из «старой» косоугольной системы координат поворотом на угол 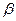вокруг оси Оz исходной декартовой системы координат против часовой стрелки. Ниже будем использовать алгебраический метод, он более компактен по сравнению с геометрическими построениями, а предыдущие построения позволяют надеяться, что у читателя при необходимости не возникнет серьёзных затруднений, как с получением необходимых результатов, так и с геометрической интерпретацией последних.

Направляющие векторы (контравариантный базис) новой косоугольной системы координат обозначим 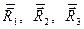. Аналитические выражения для этих векторов можно получить с помощью матрицы 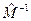(4)-(5):

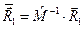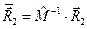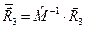, , . (22)

Здесь важно отметить, что с помощью матрицы 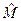рассчитывались декартовые компоненты того же самого вектора в «новой» системе координат. В соотношениях (22) нами получены проекции «нового» вектора в исходной (опорной) декартовой системе координат. В рассматриваемом случае имеем:

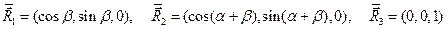. (23)

Правильность соотношений (23) легко проверяется непосредственным вычислением.

Далее необходимо повторить последовательность выкладок (11) => (21), исходя из определения «новых» направляющих векторов (контравариантный базис) повёрнутой косоугольной системы координат. Таким образом, получаем:

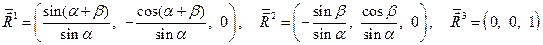(24)

- выражения для направляющих векторов взаимной системы косоугольных координат (ковариантный базис), повёрнутой относительно исходной системы косоугольных координат описанным образом. Вспоминая определения 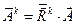и 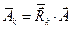, запишем выражения для контравариантных и ковариантных компонент вектора 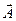в новой косоугольной системе координат:

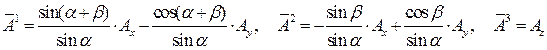, (25)

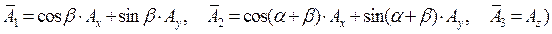. (26)

Соотношениями (25) и (26) определены матрицы перехода от проекций вектора 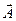на оси исходной декартовой системы координат к контравариантным и ковариантным проекциям вектора 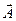в новой косоугольной системе координат:

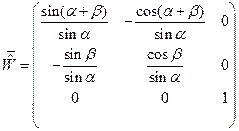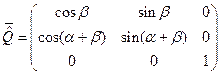, . (27)

Обе матрицы (27) являются неособенными, для каждой из них можно вычислить обратную матрицу:

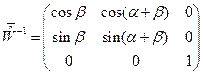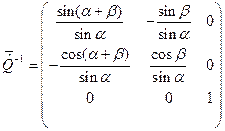, . (28)

Интересно отметить, что матрица 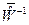является транспонированной матрицей по отношению к матрице 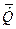, а матрица 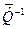- транспонированной матрицей по отношению к матрице .

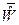С помощью матриц 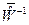и 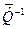устанавливаются зависимости декартовых компонент (проекций) вектора 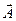от контравариантных и ковариантных компонент вектора 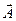в новой косоугольной системе координат:

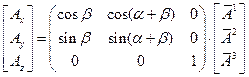, (29)

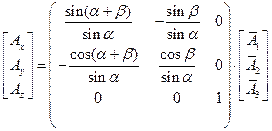. (30) Обратим внимание читателя на то, что левая часть соотношения (29) совпадает с левой частью соотношения (17). Это даёт нам право записать уравнение:

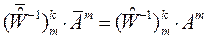. (31)

Умножим обе части уравнения (31) на матрицу 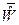слева:

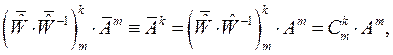(32)

в итоге получаем правило преобразования контравариантных компонент вектора при повороте исходной косоугольной системы координат:

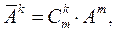
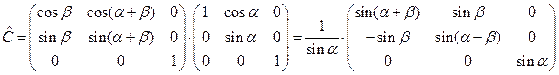. (33)

Обратное преобразование осуществляется с помощью соответствующей обратной матрицы:

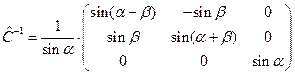. (34)

Аналогичным образом получаем правило преобразования ковариантных компонент вектора:

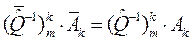, (35)

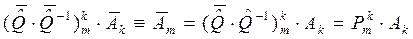, (36)

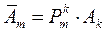, (37)

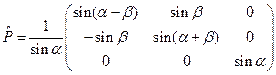. (38)

Обратное преобразование ковариантных компонент вектора можно осуществить с помощью матрицы:

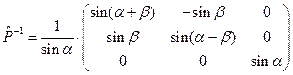. (39)

Обратим внимание читателя на два обстоятельства.

- Соотношения (33)-(34) и (38)-(39) полностью определены геометрией исходной косоугольной системы и углом поворота исходной системы в новое положение, исходная декартовая система координат сослужила нам службу и может быть отложена.

- Матрица преобразования ковариантных компонент вектора совпадает (это можно проверить непосредственным вычислением) с обратной и транспонированной матрицей преобразования контравариантных компонент вектора. Матрица преобразования контравариантных компонент вектора совпадает (это тоже можно проверить непосредственным вычислением) с обратной и транспонированной матрицей преобразования ковариантных компонент вектора.

Вектор и тензор.

Закономерности преобразованиякоординат точки пространства при переходе от одной координатной системы к другой легли в основу определения понятия «вектор»:

контравариантным (ковариантным) вектором называют одноиндексный объект, элементы которого при переходе от одной системы координат к другой преобразуются как контравариантные (ковариантные) координаты точки.

Формулы преобразования проекций вектора имеют вид:

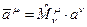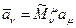, . (1)

Тензор представляет собой объект более сложного строения, он может иметь несколько индексов. В частности, для двухиндексного объекта возможно контравариантное представление 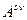, ковариантное представление 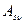и смешанное 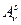. Законы преобразования тензоров второго ранга (второго порядка) имеют вид:

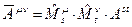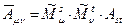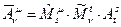, , . (2)