Проблема разложения вектора на составляющие.

Системы координат. Скалярные, векторные и тензорные величины. Преобразования Лоренца.

Положение точки на некоторой кривой линии, на поверхности или в объёме описывают с помощью «координат», полный набор которых единственным образом определяет рассматриваемое местонахождение точки. Множество положений точки является многообразием. Многообразие превращается в метрическое пространство, если задано правило определения расстояния между точками многообразия, если определена «метрика» пространства. Поскольку положение точки определяется набором координат, понятно, что метрические свойства пространства проявляются в определенных соотношениях между координатами точек. До сих пор мы пользовались, в основном, декартовыми координатами в трёхмерном пространстве, вскользь упоминая о цилиндрических и сферических координатах, каждый раз подчеркивая, что в разных системах координат одни и те же по физическому смыслу уравнения электростатики, например, имеют разную форму записи. Достаточно вспомнить выражения для градиента скалярного поля, дивергенции или ротора векторного поля и лапласиана. Освоение основных понятий и результатов специальной теории относительности невозможно без привлечения таких понятий как контравариантные и ковариантные координаты, контравариантные и ковариантные составляющие вектора и тензора. Преодоление трудности освоения новых понятий с лихвой окупается эстетическим удовольствием от совершенства картины открывающегося перед исследователем мира физических явлений. Нобелевский лауреат, известный физик-теоретик прошлого столетия Поль Дирак 3-его октября 1956 г. на доске кабинета кафедры теоретической физики МГУ им. М.В. Ломоносова написал фразу: “Physical law should have mathematical beauty” (физический закон должен быть математически изящным). Но дело не только в эстетике. Часто «сухая» абстрактная математическая форма помогает выявить физический смысл результата.

Проблема разложения вектора на составляющие.

Известно правило сложения векторных величин – правило параллелограмма.

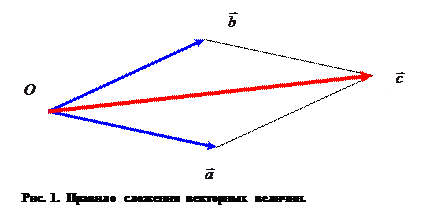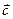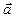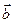Определение вектора как суммы векторов и с общим началом сводится к нахождению точки пересечения двух прямых линий, каждая из которых исходит из конца исходного вектора параллельно второму слагаемому. Это построение выполняется в плоскости, однозначно определяемой исходными векторам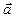и и 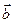. Результирующий вектор 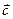является направленным отрезком, начало которого совпадает с началами исходных векторов, а конец определяется положением точки пересечения описанных прямых. Обратная задача состоит в разложении вектора 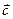на составляющие вдоль двух направлений, заданных направляющими векторам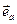и и .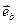

Обратная задача естественным образом связана с правилом сложения векторов. Её решение осуществляется с помощью метода параллельного проектирования. Для построения вектора 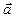из конца вектора 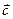проводится прямая, параллельная направляющему вектору 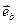, до пересечения с прямой, определяемой направляющим вектором 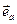.Описанная точка пересечения является концом вектора 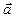. Аналогичным образом строится вектор 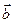как составляющая вектора 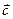по направлению 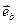. 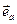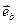Эти построения выполняются в плоскости, определяемой ориентацией направляющих векторов и с общим началом.

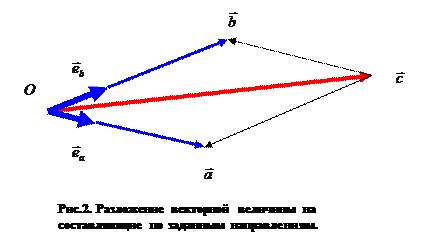
Сложение трёх векторов последовательным выполнением операции сложения двух векторов сводится к рассмотренному случаю. Разложение исходного вектора на составляющие по трём заданным некомпланарным направлениям геометрически решается с помощью метода параллельного проектирования. Рассмотрим рис. 3. Допустим, что вектор 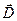необходимо разложить по трём направлениям, которые определяются векторам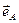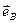и , и 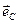. По условию указанные векторы не лежат в одной плоскости. Составляющую вектора 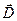по направлению 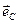построим следующим образом. Из конца вектора 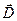проведём прямую линию, параллельную заданному вектору 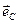, до пересечения с плоскостью, в которой расположены векторы 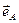и 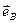. Пусть рассматриваемой точкой

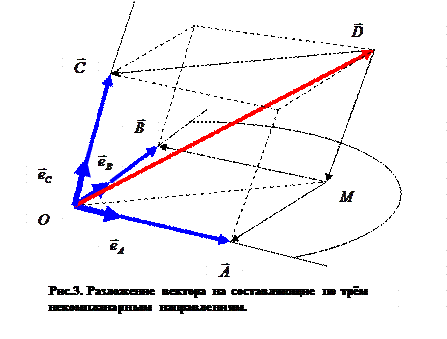
пересечения будет точка М. Соединим начало вектора 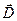- точку О - с точкой М и проведём прямую линию, параллельную отрезку ОМ через конец вектора 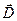до пересечения с направлением 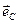. Составляющая вектора 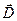по направлению 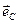- вектор 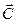- построена. Мы получили бы аналогичный результат, если бы через конец вектора 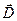провели проектирующую плоскость, параллельную плоскости, в которой расположены векторы 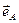и 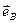, а конец вектора 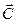определили бы как точку пересечения направления 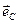с проектирующей плоскостью.

Формально вектор 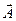можно построить с помощью проектирующей плоскости, параллельной плоскости, в которой лежат заданные векторы 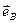и 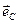, а вектор 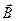- с помощью проектирующей плоскости, параллельной плоскости, в которой лежат векторы 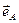и 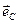. Привлекая к рассмотрению правило сложения векторов, убеждаемся, что разложение выполнено правильно.