Предельный переход под знаком интеграла Лебега
Особенно заметны преимущества интеграла Лебега над интегралом Римана, когда мы имеем дело с предельным переходом. В случае интеграла Римана перемена порядка операций интегрирования и перехода к пределу требует установить факт равномерной сходимости последовательности подынтегральных функций. В случае интеграла Лебега подобных трудностей нет. Это вытекает из трёх следующих результатов, играющих центральную роль в теории интегрирования.
Теорема(Лебега о мажорированной сходимости).
Пусть (X,S,m) – пространство с мерой, 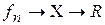 и
и 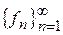 – последовательность измеримых функций, сходящаяся почти всюду к
– последовательность измеримых функций, сходящаяся почти всюду к 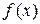 . Если существует интегрируемая функция
. Если существует интегрируемая функция 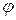 такая, что
такая, что 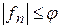 (для всех
(для всех 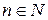 ), то f – интегрируема и
), то f – интегрируема и
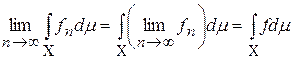 .
.
Теорема (Беппо-Леви о монотонной сходимости).
Пусть (X,S,m) – пространство с мерой и 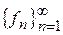 ,
, 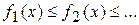 – монотонно возрастающая последовательность интегрируемых функций и пусть существует
– монотонно возрастающая последовательность интегрируемых функций и пусть существует 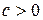 , что
, что 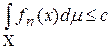 для всех
для всех 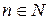 . Тогда почти всюду существует конечный предел
. Тогда почти всюду существует конечный предел 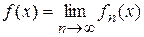 , функция f интегрируема и
, функция f интегрируема и 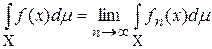 .
.
Следствие 1.Пусть 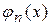 – последовательность неотрицательных интегрируемых функций и пусть числовой ряд
– последовательность неотрицательных интегрируемых функций и пусть числовой ряд 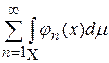 сходится. Тогда почти всюду сходится ряд
сходится. Тогда почти всюду сходится ряд 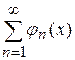 и
и
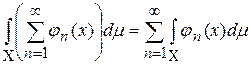 .
.
Следствие 2.Пусть 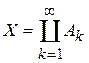 и пусть f – измеримая функция такая, что
и пусть f – измеримая функция такая, что 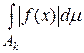 существует и ряд
существует и ряд 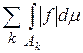 сходится. Тогда f интегрируема и
сходится. Тогда f интегрируема и 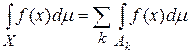 .
.
Теорема (Фату). Пусть (X,S,m) – пространство с мерой и 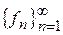 – последовательность неотрицательных интегрируемых функций,
– последовательность неотрицательных интегрируемых функций,  , обладающая свойствами:
, обладающая свойствами:
1) 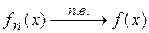 на X,
на X,
2) 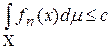 для всех n.
для всех n.
Тогда функция 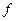 интегрируема и
интегрируема и 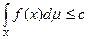 .
.
Дата добавления: 2021-07-22; просмотров: 141;










