Численное интегрирование
Основные вопросы, рассматриваемые на лекции:
1. Постановка задачи численного интегрирования
2. Квадратурные формулы Ньютона-Котеса
3. Формулы прямоугольников
4. Формула трапеций
5. Формула Симпсона
6. Квадратурные формулы Гаусса
7. Метод Монте-Карло
1. Постановка задачи численного интегрирования
Требуется вычислить определённый интеграл вида 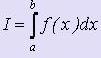 , причём функция может быть задана как в виде формулы, так и в виде таблицы.
, причём функция может быть задана как в виде формулы, так и в виде таблицы.
· Квадратурные формулы Ньютона-Котеса
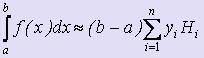 ,
,
где 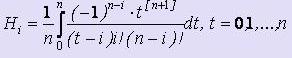 - коэффициенты Котеса.
- коэффициенты Котеса.
Эти формулы дают на одном участке интегрирования различные представления для различного числа n отрезков разбиения.
· Формулы прямоугольников
Пусть требуется вычислить интеграл 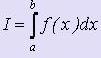 .
.
Если отрезок интегрирования [a; b] достаточно велик, то нужно разбить его на более мелкие отрезки равной длины 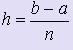 , где n - число отрезков, и заменяя на каждом из отрезков криволинейную трапецию прямоугольником, вычислить площади этих прямоугольников. Затем полученные площади нужно сложить, эта сумма и будет принята за приближённое значение искомого интеграла.
, где n - число отрезков, и заменяя на каждом из отрезков криволинейную трапецию прямоугольником, вычислить площади этих прямоугольников. Затем полученные площади нужно сложить, эта сумма и будет принята за приближённое значение искомого интеграла.
Что касается построения прямоугольников, то их можно строить по-разному: можно проводить перпендикуляр до пересечения с кривой f (x) из правого конца каждого отрезка (Рис. 1), можно - из левого конца (Рис. 2)
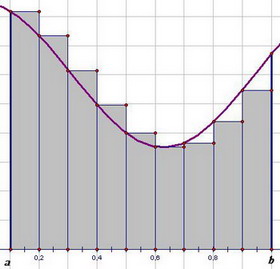 Рис. 1 Рис. 1
| 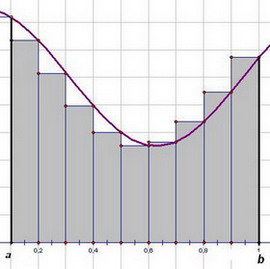 Рис. 2 Рис. 2
|
В зависимости от этого формулы для вычисления несколько различны и носят название формулы прямоугольников с правыми или левыми ординатами соотвественно:
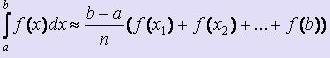
(формула "правых" прямоугольников)
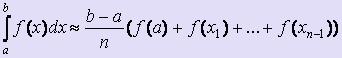
(формула "левых" прямоугольников)
Существует ещё формула "средних" прямоугольников: 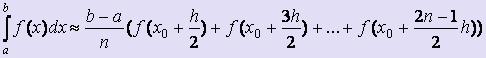 , для которой построение прямоугольников осуществляется через середины каждого из отрезков разбиения:
, для которой построение прямоугольников осуществляется через середины каждого из отрезков разбиения:
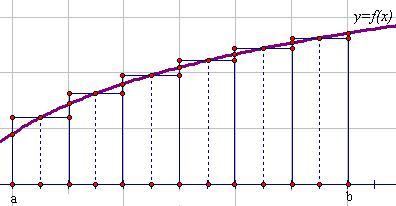
· Формула трапеций
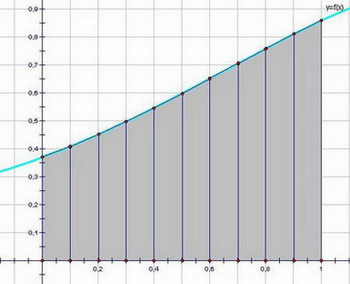
Идея метода аналогична той, что представлена в методе прямоугольников. Отличие заключается в том, что на каждом отрезке разбиения криволинейная трапеция заменяется на обычную трапецию, площадь которой вычисляется по формуле 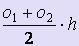 , где o1 и o2 - основания трапеции. Вычисляя и суммируя площади всех трапеций, получаем приближённое значение искомого интеграла: , где o1 и o2 - основания трапеции. Вычисляя и суммируя площади всех трапеций, получаем приближённое значение искомого интеграла:
| 
|
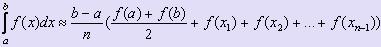
· Формула Симпсона
Заменяя на каждом отрезке разбиения часть кривой y = f (x) на параболическую кривую, вычисляя площади получившихся фигур и суммируя их, получим формулу Симпсона:
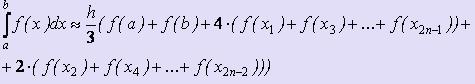 ·
·
· Квадратурные формулы Гаусса
Традиционно при получении квадратурных формул Гаусса в исходном интеграле выполняется замена переменной, переводящая интеграл по отрезку [a; b] в интеграл по отрезку [-1; 1]:
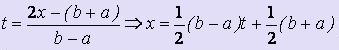 .
.
Тогда 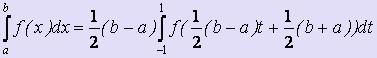 .
.
Будем использовать линейную интерполяцию подынтегральной функции.
Если вместо отрезка [-1; 1] взять в качестве узлов интерполяции подвижные узлы t1, t2, то нужно выбрать эти значения так, чтобы площадь трапеции, ограниченнной сверху прямой, проходящей через точки A1 (t1, φ(t1) ) и A2 (t2, φ(t2) ) была равной интегралу от любого многочлена некоторой наивысшей степени.
Полагая, что это многочлен третьей степени, вычислим t1, t2, которые получаются равными 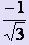 и
и 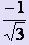 , отличаясь лишь нумерацией значений.
, отличаясь лишь нумерацией значений.
Далее разбивая отрезок интегрирования на n частей, применяя к каждому из них описанную выше идею, можно получить формулу Гаусса: 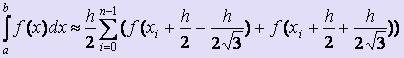
· Метод Монте-Карло
Идея метода:
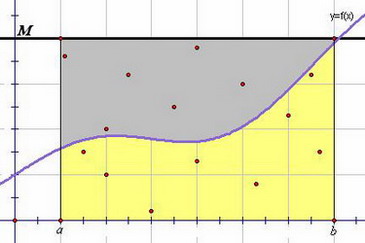
Пусть f (x) > 0 (для простоты рассуждений). Возьмём число M, такое чтоf (x)  M для любого x из отрезка [a; b]. На графике - это прямая y = M. Используя счётчик случайных чисел можно получить точки, случайно и равномерно распределённые в прямоугольнике, образованном: M для любого x из отрезка [a; b]. На графике - это прямая y = M. Используя счётчик случайных чисел можно получить точки, случайно и равномерно распределённые в прямоугольнике, образованном:
| 
|
- отрезком [a; b] оси Ох
- отрезком, принадлежащим прямой y = M длины b-a
- отрезками, принадлежащими прямым х = a и x = b, заключёнными между осью Ох и прямой y = M.
Координаты таких точек вычисляются по формулам: 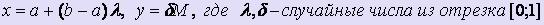 .
.
Если найдено таким образом n точек и k из них принадлежит криволинейной трапеции, ограниченной кривой y = f (x), прямыми x = a, x = b и осью Ох, то, с учётом того, что при больших n распределение точек по прямоугольнику близко к равномерному, то отношение k / nприближённо равно отношению площади криволинейноё трапеции к площади прямоугольника: 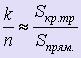
При этом
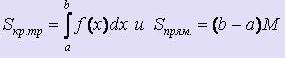
Подставляя значения площадей и выражая интеграл, получаем: 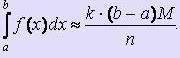
Дата добавления: 2017-05-02; просмотров: 2563;










