Схема метода ветвей и границ для общей задачи дискретного программирования.
Поиск с возвратами
Широко распространенным приемом, используемым для построения эффективных алгоритмов решения оптимизационных задач ДО является поиск с возвратами (backtracking)[1].
Метод поиска с возвратами постоянно пытается расширить частичное решение с помощью присвоения значений переменным. Если расширение текущего частичного решения невозможно, то возвращаются к более короткому частичному решению и пытаются снова его продолжить.
В общем случае полагаем, что решение задачи состоит из вектора 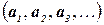 конечной, но неопределенной длины, удовлетворяющего некоторым ограничениям. Каждое
конечной, но неопределенной длины, удовлетворяющего некоторым ограничениям. Каждое 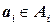 , где
, где 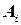 ‑ конечное линейно упорядоченное множество. Таким образом, при исчерпывающем поиске должны рассматриваться элементы множества
‑ конечное линейно упорядоченное множество. Таким образом, при исчерпывающем поиске должны рассматриваться элементы множества 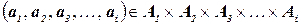 для
для 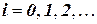 в качестве возможных решений. В качестве исходного частичного решения примем пустой вектор
в качестве возможных решений. В качестве исходного частичного решения примем пустой вектор 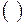 и на основании имеющихся ограничений выясним, какие элементы из
и на основании имеющихся ограничений выясним, какие элементы из 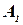 являются кандидатами в
являются кандидатами в 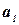 . Обозначим это подмножество кандидатов через
. Обозначим это подмножество кандидатов через 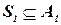 . В результате имеем частичное решение
. В результате имеем частичное решение 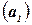 . В общем случае для расширения частичного решения от
. В общем случае для расширения частичного решения от 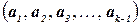 до
до 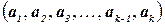 кандидаты на роль
кандидаты на роль 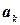 выбираются из
выбираются из 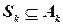 . Если частичное решение
. Если частичное решение 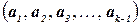 не представляет возможности для выбора элемента
не представляет возможности для выбора элемента 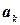 , то
, то 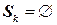 ; возвращаемся и выбираем новый элемент
; возвращаемся и выбираем новый элемент 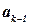 . Если новый элемент
. Если новый элемент 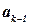 выбрать нельзя, возвращаемся еще дальше и выбираем новый элемент
выбрать нельзя, возвращаемся еще дальше и выбираем новый элемент 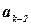 и т.д. Этот процесс удобно представлять в терминах прохождения дерева поиска в глубину. Процедура поиска с возвратами для нахождения всех решений представлена на рис. 6.1.
и т.д. Этот процесс удобно представлять в терминах прохождения дерева поиска в глубину. Процедура поиска с возвратами для нахождения всех решений представлена на рис. 6.1.
|
Рис. 6.1. Алгоритм поиска с возвратами.
Поиск с возвратами имеет экспоненциальную сложность, так как из предположения, что все решения имеют длину не более 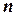 , исследованию подлежат в худшем случае
, исследованию подлежат в худшем случае 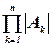 элементов. В предположении, что все
элементов. В предположении, что все 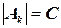 ‑ константы, получаем экспоненциальную сложность
‑ константы, получаем экспоненциальную сложность 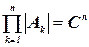 . Понятно, что поиск с возвратами представляет собой только общий метод. Поэтому к нему нужно относиться как к вычислительной схеме, используемой для решения задачи. Схема должна быть хорошо приспособлена к конкретной задаче, так чтобы полученный в результате алгоритм подходил для практического использования.
. Понятно, что поиск с возвратами представляет собой только общий метод. Поэтому к нему нужно относиться как к вычислительной схеме, используемой для решения задачи. Схема должна быть хорошо приспособлена к конкретной задаче, так чтобы полученный в результате алгоритм подходил для практического использования.
При решении задач дискретной оптимизации характерным приемом является разбиение задачи на подзадачи, или ветвление. Цель разбиения исходной задачи на подзадачи состоит в понижении размерности и/или упрощении исходной задачи. Полученные подзадачи либо решают, либо, в свою очередь, применяют к ним процедуру ветвления. Решение всей задачи получается в результате решения всех подзадач наиболее низкого уровня ветвления.
Схема метода ветвей и границ для общей задачи дискретного программирования.
Метод ветвей и границ (branch and bound)[2] представляет собой систематическую схему неявного перебора конечного числа допустимых решений ЗЦЛП. Хотя теоретически размер дерева перебора является экспоненциальным от параметров задачи, в большинстве случаев метод исключает большое число допустимых решений. Основные шаги метода ветвей и границ
(1) Выбор/Исключение одной или более текущих задач из списка задач-кандидатов.
(2) Релаксация (ослабление) выбранной текущей задачи для получения верхней границы (оценки сверху) (для задачи максимизации) целевой функции текущей задачи.
(3) Зондирование, если это возможно, текущей задачи.
(4) Стратегия ветвления: Если текущая задача не зондируется, процедура ветвления строит подзадачи, дкоторые добавляются к списку задач-кандидатов.
Описанные шаги повторяются до тех пор, пока список задач-кандидатов не станет пустым. Метод ветвей и границ последовательно исследует задачи, которые добавляются в список задач-кандидатов или исключаются из этого списка. Опишем подробнее алгоритм ветвей и границ для решения задачи ЦЛП.
0. Инициализация. Вначале список задач-кандидатов содержит только исходную задачу ЦЛП следующего вида
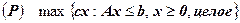 .
.
Через 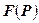 обозначим множество допустимых решений задачи
обозначим множество допустимых решений задачи 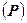 , ачерез
, ачерез 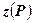 ‑ оптимальное значение целевой функции задачи
‑ оптимальное значение целевой функции задачи 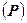 .Для любого
.Для любого 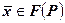 положим
положим 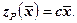
Наилучшее решение, известное для задачи 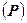 ,называется текущимрекордом.Соответствующее значение ЦФ обозначим
,называется текущимрекордом.Соответствующее значение ЦФ обозначим 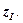 Для данной задачи ДО (P) значение целевой функции рекорда
Для данной задачи ДО (P) значение целевой функции рекорда 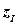 находится с помощью какой-либо эвристики[3] (если же допустимое решение задачи (P) не может быть найдено, нужно положить
находится с помощью какой-либо эвристики[3] (если же допустимое решение задачи (P) не может быть найдено, нужно положить 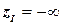 ). Внести в список задач-кандидатов задачу (P):
). Внести в список задач-кандидатов задачу (P): 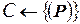 .
.
1. Оптимальность. Если 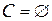 и
и 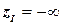 , то задача (P) недопустима, конец вычислений. Если
, то задача (P) недопустима, конец вычислений. Если 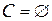 и
и 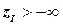 , то рекорд является оптимальным решением задачи (P), конец вычислений.
, то рекорд является оптимальным решением задачи (P), конец вычислений.
2. Выбор/Исключение. Используя одно из правил выбора задач-кандидатов, выбрать и удалить задачу (P) из списка 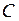 . Выбранная задача называется в дальнейшем задача-кандидат (ЗК). Алгоритм кончает работу, если список задач-кандидатов пуст. В самом начале нет проблем с выбором, так как список задач-кандидатов содержит лишь одну задачу
. Выбранная задача называется в дальнейшем задача-кандидат (ЗК). Алгоритм кончает работу, если список задач-кандидатов пуст. В самом начале нет проблем с выбором, так как список задач-кандидатов содержит лишь одну задачу 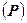 .Однако во время работы алгоритма список задач-кандидатов может содержать много задач и поэтому нужно использовать правило выбора текущей задачи. Соответствующие правила выбора, называющиеся также стратегиями ветвления, рассматриваются далее.
.Однако во время работы алгоритма список задач-кандидатов может содержать много задач и поэтому нужно использовать правило выбора текущей задачи. Соответствующие правила выбора, называющиеся также стратегиями ветвления, рассматриваются далее.
В принципе могут быть одновременно выбраны и исключены сразу несколько задач из списка задач-кандидатов. Однако большинство версий алгоритма ветвей и границ выбирает только одну задачу из списка задач-кандидатов, в дальнейшем так и будем считать.
Время счета для алгоритма ветвей и границ существенно зависит от порядка, в котором изучаются задачи из списка задач-кандидатов. Здесь могут быть использованы различные эвристические правила. На практике обычно используются для выбора задач две стратегии общего назначения:
(А) Выбрать задачу, добавленную последней в список задач-кандидатов. Это правило LIFO (last-in-first-out, т.е. первой выбирается задача, добавленная последней в в список) называется также поиском в глубину, т.к. добавление задачи-кандидата увеличивает глубину текущего дерева перебора.
(B) Выбрать задачу из списка задач-кандидатов с наибольшей верхней границей (для задачи максимизации[4]). Для применения этого правила задачи, включаемые в список задач-кандидатов, должны иметь верхние границы. Это может быть осуществлено с помощью релаксаций.
3. Граница. Получить верхнюю границу для целевой функции задачи (P) с помощью релаксации (PR) задачи (P) или с помощью применения специальных правил. Если (PR) недопустима – вернуться к шагу 1. В противном случае, 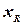 ‑ опимальное решение (PR).
‑ опимальное решение (PR).
4. Зондирование. Если 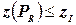 , вернуться к шагу 1. Иначе, если
, вернуться к шагу 1. Иначе, если 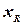 допустимо для задачи (P) и
допустимо для задачи (P) и 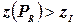 , положить
, положить 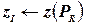 , обновить рекорд (положив его равным
, обновить рекорд (положив его равным 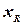 ) и вернуться к шагу 1. И, наконец, если
) и вернуться к шагу 1. И, наконец, если 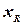 допустимо для задачи (P), но
допустимо для задачи (P), но 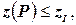 вернуться к шагу 1.
вернуться к шагу 1.
5. Разбиение. Используя правила разбиения или ветвления, разбить (P) на 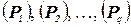 , положить
, положить 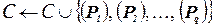 и вернуться к шагу 1.
и вернуться к шагу 1.
Для единообразного изложения точных методов ДО будем использовать схему Джеффриона и Марстена[5], которая, по нашему мнению, является одной из самых удачных. Излагать эту схему будем применительно к задаче частично целочисленного линейного программирования в матричной форме записи
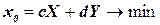 (6.1)
(6.1)
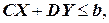 (6.2)
(6.2)
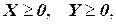 (6.3)
(6.3)
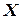 — целочисленный вектор. (6.4)
— целочисленный вектор. (6.4)
Для простоты изложения множество допустимых решений (6.2) ‑ (6.4) будем считать непустым и ограниченным.
Общая структура схемы Джеффриона и Марстена изображена на блок-схеме 6.1. Она состоит из следующих этапов.
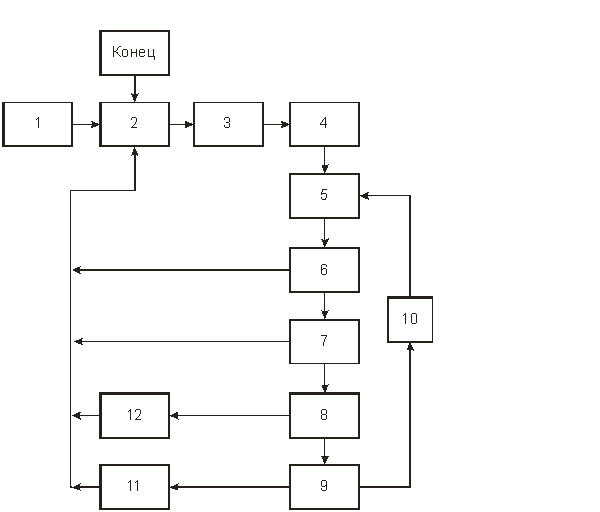
Блок-схема 6.1. Схема Джеффриона и Марстена.
1. Начать список задач-кандидатов (ЗК) для ветвления 2, внеся в него задачу (6.1) ‑ (6.4) и положить рекорд 3 равным +∞.
2. Пуст ли список? Если пуст, то задача решена. Если непуст, переходим к шагу 3.
3. Выбрать ЗК для ветвления.
4. Релаксация (т. е. ослабление) условий целочисленности (переход от задачи частично-целочисленного программирования к соответствующей оценочной задаче линейного программирования).
5. Решение релаксированной задачи.
6. Пусто ли множество решений релаксированной задачи?
Если пусто, то переходим к шагу 2. Если непусто, переходим к шагу 7.
7. Оценка, полученная после решения ЗК, лучше рекорда? Если лучше, переходим к шагу 8. Если не лучше, переходим к шагу 2.
8. Получено ли оптимальное решение ЗК? Если получено, переходим к шагу 12. Если не получено, переходим к шагу 9.
9. Продолжать ли решение ЗК? Если да, то переходим к шагу 10. Если нет, переходим к шагу 11.
10. Модифицировать релаксацию (например, с учетом зафиксированных значений для некоторых из целочисленных переменных). Перейти к шагу 5.
11. Разветвить ЗК на задачи-потомки и занести их в список ЗК. Перейти к шагу 2.
12. Заменить рекорд и очистить список ЗК. Перейти к шагу 2.
Поясним общую схему.
1. Шаги 5, 6, 7, 8, 9, 10 ‑ это отдельные элементы процедуры оценивания.
2. Схема состоит из следующих основных элементов:
а) ветвление ‑ выбор ЗК и построение рекорда;
б) релаксация ‑ построение оценочных задач;
в) построение оценок.
3. Возможны различные способы ветвления, среди которых особо распространены:
α) покомпонентное ветвление;
β) ветвление с использованием дихотомии;
γ) сочетание α) и β);
4. Возможны различные стратегии ветвления (выбора ЗК), в частности:
а) ветвление по наименьшей нижней оценке;
б) одностороннее ветвление (ветвление по заранее намеченному пути);
в) ветвление по наименьшей нижней оценке среди множеств, достроенных на последнем шаге (или нескольких последних шагах);
г) ветвление в зависимости от разности между наименьшей нижней оценкой для множеств, построенных на последнем шаге, и множеств, построенных на предшествующих шагах;
д) эвристическое ветвление;
е) ветвление по вероятностным характеристикам;
ж) комбинация некоторых стратегий, перечисленных выше.
5. Оценивание:
а) оценки, получаемые через решение задач линейного программирования, можно существенно улучшить, если использовать штрафные добавки (об этом будет сказано ниже);
б) для определения оценок можно использовать также и эвристические процедуры.
Несмотря на кажущуюся простоту метода ветвей и границ, реализация этой схемы для конкретной задачи ДО является нетривиальной, так как для ее реализации требуются:
(A) стратегии релаксации с эффективными решателями этих релаксаций.
(B) Эффективные структуры данных для поддержания списка задач-кандидатов.
(C) Разумнык стратегии выбора перспективных задач-кандидатов.
(D) Стратегии разбиения или ветвления, позволяющие эффективно сокращать дерево перебора.
Одной из важнейших является задача разработки стратегии релаксации (A), состоящей в поиске «хороших релаксаций», которые можно решить существенно проще, чем исходную задачу и в то же время получить как можно более точные верхние границы.
Дата добавления: 2016-06-05; просмотров: 2882;











