Решение матричной игры в смешанных стратегиях
Игра, заданная некоторой матрицей, может не иметь седловой точки.
Пример 3Рассмотрим платёжную матрицу
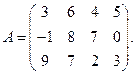
Для первого игрока находим максимин
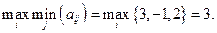
Для второго игрока находим минимакс
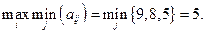
Следовательно, минимакс и максимин не совпадают, т.е. положения равновесия в чистых стратегиях не существует.
Если среди чистых стратегий решения игры нет, то для его нахождения используются смешанные стратегии. Справедлива теорема.
Теорема Ноймана(основная теорема теории игр)Каждая конечная игра имеет,по крайней мере, одно оптимальное решение, возможно среди смешанных стратегий.
При этом если 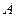 - платежная матрица,
- платежная матрица, 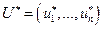 - оптимальная смешанная стратегия первого игрока, a
- оптимальная смешанная стратегия первого игрока, a 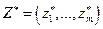 - второго, то число
- второго, то число
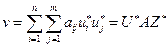
является ценой игры.
Определение.Если чистая стратегия входит в смешанную с ненулевой вероятностью, то она называется активной
Активные стратегии обладают свойством, выражаемым следующей теоремой.
Теорема(об активных стратегиях) Если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остаётся неизменным и равным цене игры 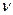 , если второй игрок не выходит за пределы своих активных стратегий.
, если второй игрок не выходит за пределы своих активных стратегий.
Дата добавления: 2017-04-05; просмотров: 1827;










