Решение матричной игры в чистых стратегиях
Математиком А. Вальдом был сформулирован принцип суть которого состоит в том, что при принятии решения в условиях неопределенности разумно исходить из того, что сложится наименее благоприятная ситуация. Исходя из этого принципа игрок 1 может рассуждать следующим образом:
«Предположим, что я выберу 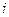 -ю стратегию, тогда в худшем для меня случае я получу выигрыш величиной
-ю стратегию, тогда в худшем для меня случае я получу выигрыш величиной
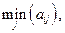
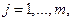
где 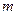 -количество строк в матрице игры, т.е. количество чистых стратегий 2-го игрока. Тогда я должен выбрать такую строку, т.е.
-количество строк в матрице игры, т.е. количество чистых стратегий 2-го игрока. Тогда я должен выбрать такую строку, т.е. 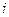 -ю стратегию (
-ю стратегию ( 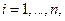
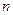 - количество столбцов в матрице игры), при которой этот минимум максимальный».
- количество столбцов в матрице игры), при которой этот минимум максимальный».
Определение.Число 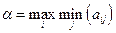 называется нижней ценой игры или максимином, а соответствующая ему стратегия (строка) - максиминной.
называется нижней ценой игры или максимином, а соответствующая ему стратегия (строка) - максиминной.
Аналогично, второй игрок, также исходя из наихудшего исхода, должен рассуждать следующим образом:
«Предположим, что я выберу 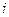 -ю стратегию, тогда в худшем для меня случае я потеряю величину
-ю стратегию, тогда в худшем для меня случае я потеряю величину
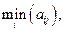
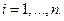
Тогда я должен выбрать такой столбец, т.е. 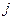 -ю стратегию, при которой этот максимум минимальный»
-ю стратегию, при которой этот максимум минимальный»
ОпределениеЧисло 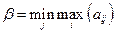 называется верхней ценой игры или минимаксом, а соответствующая ему стратегия игрока (столбец) - минимаксной.
называется верхней ценой игры или минимаксом, а соответствующая ему стратегия игрока (столбец) - минимаксной.
ТеоремаНижняя цена игры не превосходит верхней цены игры.
Если для некоторой игры верхняя и нижняя цены равны, т.е. выполняется 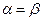 , или что то же самое
, или что то же самое
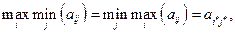
где 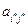 - соответствующий элемент матрицы игры, то очевидно для этого элемента выполняется неравенство
- соответствующий элемент матрицы игры, то очевидно для этого элемента выполняется неравенство
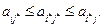
Сравнивая это неравенство с (3) видим, что оказывается ситуация 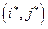 является равновесной, т.е. оптимальной, т.е. решением игры. Величина
является равновесной, т.е. оптимальной, т.е. решением игры. Величина 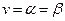 при этом, очевидно, является ценой игры, т.е. рассматриваемые принципы максимина и минимакса приводят к оптимальному и равновесному состоянию. Это еще раз свидетельствует об обоснованности их использования при принятии решений.
при этом, очевидно, является ценой игры, т.е. рассматриваемые принципы максимина и минимакса приводят к оптимальному и равновесному состоянию. Это еще раз свидетельствует об обоснованности их использования при принятии решений.
ОпределениеИгра, для которой 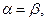 называется игрой с седловой точкой.
называется игрой с седловой точкой.
Пример 2Для игровой матрицы из примера 4.1 найти седловые точки, если они есть. Нахождение нижней и верхней цен игры, равно как и проверка существования седловых точек и их нахождение, для матричных игр удобно проводить по следующей схеме
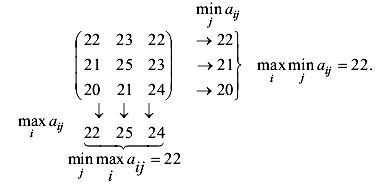
Видно, что максимин имеет место в 1-й строке, т.е. при первой стратегии 1-го игрока. Минимакс - в первом столбце, т.е. при 1-й стратегии 2-го игрока. При этом они совпадают, т.е. имеется седловая точка. Это ситуация 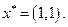
Дата добавления: 2017-04-05; просмотров: 1753;










