Формы представления расписаний
В расписаниях для рассматриваемой совокупности действий, операций, работ указываются моменты их начала, а иногда и моменты окончания или даже каких-то промежуточных состояний их выполнения во времени.
При необходимости указываются также те блоки системы, которые реализуют выполнение соответствующих действий, операций, работ.
Достаточно широко распространены формы представления календарных планов в виде так называемых сетевых графиков (стрелочных диаграмм). Сетевые графики чаще всего используются для представления календарных планов выполнения сложных разработок, индивидуальных заказов особой важности, проектирования или строительства уникальных объектов большим количеством исполнителей.
Для таких разработок, проектов, строек особо важно представить взаимоувязку во времени выполнения отдельных работ или их комплексов. Этим целям служат сетевые графики. Образец сетевого графика в так называемой форме «работы-вершины» представлен на рис. 9.1. Вершинами сетевого графика обозначены отдельные работы, на которые расбивается общий комплекс работ, дуги представляют информацию о взаимозависимости очередности выполнения работ. Логическая взаимозависимость очередности выполнения работ, представленная сетевым графиком, облегчает прежде всего распараллеливание комплекса разработок, распределение работ между исполнителями.
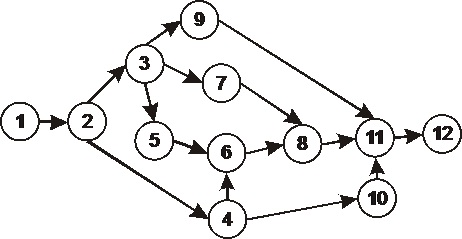
Рис. 9.1. [17, с.20]. Сетевой график разработки и внедрения задачи (программного комплекса) в АСУ. Работы: 1 — предварительное определение перечня и структуры выдаваемых документов, информационных массивов и характера их использования; 2 — разработка общей схемы решения задачи, утверждение перечня и форм выдаваемых документов, выдача задания на программирование, корректировку базовых массивов и первичных документов и т. п.; 3 — определение структур данных и способов кодирования информации; 4 — обеспечение формирования первичных данных; S — обеспечение формирования нормативных массивов; 6 — обеспечение формирования базовых массивов; 7 — разработка программного обеспечения; 8 — отладка программ; 9 — техническое обеспечение решения задачи; 10 — организационное обеспечение решения задачи; 11 — опытно-промышленная проверка; 12 — корректировка по результатам проверки.
Масштабное представление продолжительности и сроков выполнения работ используется в сетевых графиках в так называемой форме «вершины-события». В сетевых графиках в форме «вершины-события» работы отображаются дугами, а вершины отделяют работы друг от друга — их принято отождествлять с некоторыми событиями. Дуги, исходящие из некоторой вершины, соответствуют работам, которые могут быть начаты только после того, как совершилось событие, представленное этой вершиной (т. е. закончены все работы, соответствующие стрелкам, входящим в эту вершину). На рис. 9.2 дано такое представление сетевого графика (идентичного графику рис. 9.1) в форме «вершины-события».
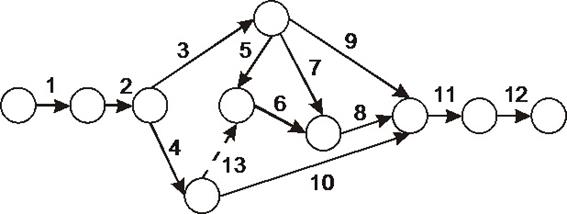
Рис. 9.2. Представление сетевого графика в форме «вершины- события» [17, с.20].
Из графика в форме «вершины-работы» можно всегда получить график в форме «вершины-события» и наоборот. Всегда осуществим и обратный переход. Неудобством второго представления является то, что для отражения очередности выполнения работ приходится вводить так называемые «фиктивные работы» (работа 13 на рис. 9.2). Фиктивные работы вводятся, в частности, для устранения случаев двух или нескольких параллельных дуг, выходящих из одной и той же и входящих в одну и ту же вершину.
Графические представления расписаний обычно сопровождаются таблицами с численными характеристиками графиков. Во многих случаях табличное представление является общепринятым, в достаточной мере наглядным и не требующим дополнительных пояснений ‑ расписание учебных занятий, футбольный календарь, расписание работы учреждений и т. п.
Диаграмма Гантта.
Одним из способов представления расписаний и календарных графиков являются диаграммы Гантта [17, с.18]. Они представляют совокупность лент или полос, расположенных вдоль оси времени, при этом каждая лента соответствует одной операции какой-либо работы. Длины этих лент равны длительностям операций, а начало ленты совпадает с началом операции.
Используются два вида этих диаграмм: диаграммы Гантта для работ и диаграммы Гантта для машин. На диаграммах для работ каждой работе соответствует ось времени, ленты на ней соответствуют операциям данной работы, выполняемым последовательно на различных машинах. На этих лентах проставляется номер машины, выполняющей эту операцию.
На диаграммах для машин на одной оси лентами изображаются все операции, выполняемые последовательно на данной машине для различных работ. На каждой ленте ставится номер работы, которой принадлежит данная операция.
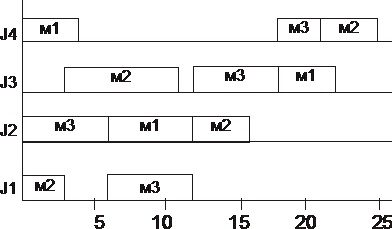
На рисунке 9.3 приведен пример диаграмм Гантта. Данные для него содержатся в таблице 9.1. В ней для каждой работы задана последовательность машин, на которых выполняются операции этой работы (технологический маршрут), и в скобках приведены длительности этих операций. Очередность выполнения операций различных работ на каждой машине, то есть собственно расписание, задана:
М1: 4, 2, 3;
М2: 1, 3, 2, 4;
М3: 2, 1, 3, 4;
На рисунке 9.3 изображены графики Гантта для этого расписания.
Таблица 9.1.– Технологические маршруты для четырех работ и трех машин
| Работы | Операции: машина и длительность | ||
| J1 | M2 (3) | M3 (7) | |
| J2 | M3 (5) | M1 (6) | M2 (4) |
| J3 | M2 (8) | M3 (6) | M1 (4) |
| J4 | M1 (4) | M3 (3) | M2 (4) |
А)
В)
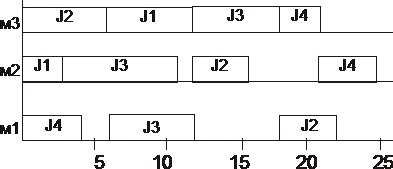
Рис. 9.3. Диаграммы Гантта для примера в таблице 9.1:
А) для работ; В) для машин
9.4. Календарное планирование с ограниченными ресурсами.
Задачи календарного планирования возникают в различных сферах деятельности, в том числе при проектировании новых изделий и запуске их в производство, составлении расписаний движения транспорта, планировании графиков выпуска и доставки продукции, разведке и освоении месторождений полезных ископаемых и т. д. Разнообразие приложений делает это направление весьма актуальным как в области разработки математических моделей, так и и методов оптимизации.
Научный подход к календарному планированию проектов предложен и применен в конце 50-х годов прошлого века. Были разработаны такие технологии как PERT (Project Evaluation and Review Technique)[5] и CPM (Critical Path Method)[6] (в отечественной литературе СПУ – сетевое планирование и управление). Характерной особенностью этих технологий является представление проекта в виде комплекса взаимосвязанных работ. Цель этих методов – минимизировать время выполнения проекта, предполагая, что необходимые для выполнения ресурсы доступны в необходимых количествах. Однако возможности указанных разработок были ограничены, так как в них не учитывались реальные ограничения на используемые ресурсы, а был учтен лишь временной аспект.
Известно, что большинство задач календарного планирования с учетом ограничений на ресурсы являются NP-трудными. В настоящее время продолжаются исследования указанных задач календарного планирования, выделяются полиномиально разрешимые случаи, разрабатываются точные и приближенные методы их решения[7]. Особую актуальность эти задачи приобретают при планировании крупномасштабных проектов, требующих больших затрат ресурсов[8].
Среди подходов к получению оптимальных решений задач календарного планирования следует выделить схему динамического программирования [23]. Другим перспективным направлением является сведение задач построения расписаний к задачам ЦЛП.
Задачи календарного планирования с ограничениями па ресурсы можно разбить два класса. К первому относятся задачи с временными критериями (общее или средневзвешенное время завершения всех работ, штраф за нарушение директивных сроков, число невыполненных в срок работ и т. д.[9]
Ко второму классу ‑ задачи с критериями, связанными с эффективным использованием ресурсов или получением прибыли, в частности, задачи минимизации общего потребления ресурсов, сглаживания потребляемых ресурсов, максимизации чистой приведенной прибыли[10].
Ограниченные ресурсы, используемые при выполнении работ, в основном делятся на возобновимые и складируемые. Возобновимые ресурсы доступны в каждый момент времени. При этом общий расход ресурса, требуемого для выполнения всех работ в рассматриваемый момент времени, не должен превосходить имеющегося объема ресурса. Представителями данного типа ресурсов являются рабочая сила, оборудование, производственные мощности и т. п. Складируемые ресурсы в отличие от возобновимых ресурсов доступны на протяжении всего проекта. В каждый период времени невостребованный объем складируемого ресурса переходит на следующий период времени. При этом в каждый момент времени должен сохраняться баланс между потребляемым и выделяемыми объемами ресурсов. Примером данного вида ресурсов могут служить материалы с длительным сроком хранения: финансы, сырье и т. д.
Наиболее изучена задача календарного планирования с возобновимыми ресурсами и критерием общего времени завершения всех работ. Для данной задачи предложены алгоритмы точного и приближенного решений. Однако задачи такого типа с другими критериями оптимизации исследованы относительно слабо, поэтому возникает необходимость в построении как точных, так и приближенных алгоритмов решения таких задач.
В связи со сложностью рассматриваемых задач значительное число исследований посвящено разработке приближенных алгоритмов с гарантированной оценкой точности. Особое значение имеют аппроксимационные схемы, с помощью которых за полиномиальное время от длины входа можно получить решение задач с любой наперед заданной точностью. Построение аппроксимационных схем решения NP-трудных задач является одним из перспективных направлений дискретной оптимизации.
Дата добавления: 2016-06-05; просмотров: 2560;










