Примеры задач, приводящих к дифференциальным уравнениям.

Решение задач прикладного характера обычно состоит из трех частей:

1) составления дифференциального уравнения;

2) решение этого уравнения;

3) исследование решения.

При решении геометрических задач полезно пользоваться следующей последовательностью действий:

1) сделать чертеж и ввести обозначения. Например, f(x) – уравнение искомой линии и т.п.

2) отделить условия, имеющие место в произвольной точке искомого геометрического места, от условий, имеющих место лишь в отдельных фиксированных точках ( т.е. выделить начальные условия).

3) выразить все упомянутые в задаче величины через x,y, 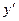, учитывая при этом геометрический смысл производной.

4) на основании условия задачи составить дифференциальное уравнение семейства искомых кривых.

5) найти общее решение дифференциального уравнения, а затем по начальным условиям найти конкретную интегральную кривую.

При решении физических задач полезно пользоваться следующей последовательностью действий:

1) Установить какому закону подчиняется процесс.

2) Решить, что выбрать за независимое переменное и что за искомую функцию.

3) Исходя из условия задачи, определить начальные условия.

4) Выразить все фигурирующие в задаче величины, используя при этом физический смысл производной как скорость изменения переменной в изучаемом процессе.

5) Исходя из условия задачи и на основании физического закона, которому подчиняется данный процесс, составить дифференциальное уравнение.

6) Найти общий интеграл дифференциального уравнения.

7) По начальным условиям найти частное решение.

Примеры.

Найти уравнение кривой, проходящей через точку Р(1;2), для которой отрезок касательной между точкой касания и осью Ох делится пополам в точке пересечения с осью Оу. (геометрическая задача).

Сосуд объемом 40 л содержит воздух (80 % азота, 20% кислорода). В сосуд втекает каждую секунду 0,2 л азота, который непрерывно размешивается, и вытекает такое же количество смеси. Через какое время в сосуде будет 99 % азота? (физическая задача).