Применение интеграла Мора при продольно-поперечном изгибе.
Как известно, интеграл Мора получен из принципа возможных перемещений. Поскольку этот принцип применим и для продольно-поперечного изгиба, то формула Мopa также справедлива. При потере устойчивости критическая деформация системы происходит в условиях продольно-поперечного изгиба.
Если при расчете устойчивости рамной или балочной конструкции пренебречь, как это принято при обычных расчетах, деформациями сдвига и обжатия оси, то интеграл Мopa запишется следующим образом:
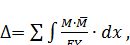 (121)
(121)
где 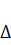 - действительное перемещение «сжато-изогнутой» системы;
- действительное перемещение «сжато-изогнутой» системы;
M - ордината изгибающих моментов с учетом продольно- поперечного изгиба;
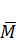 - ордината единичной эпюры моментов без учета продольного изгиба, т.е. от единичной поперечной нагрузки.
- ордината единичной эпюры моментов без учета продольного изгиба, т.е. от единичной поперечной нагрузки.
Для определения перемещения по формуле (122) при продольном изгибе необходимо вычислить интеграл 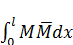 . Будем считать, что нормальная сила N и жесткость EY на участке «L» м заданной рамы постоянны. Произвольный участок AB с приложенными по концам продольной силой N и моментами а и b показан на рис.66.
. Будем считать, что нормальная сила N и жесткость EY на участке «L» м заданной рамы постоянны. Произвольный участок AB с приложенными по концам продольной силой N и моментами а и b показан на рис.66.
Запишем дифференциальное уравнение изгиба сжато-изогнутого стержня с постоянной продольной силой (123)
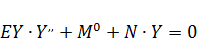 .
.
Продифференцируем уравнение дважды:
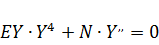 . (124)
. (124)
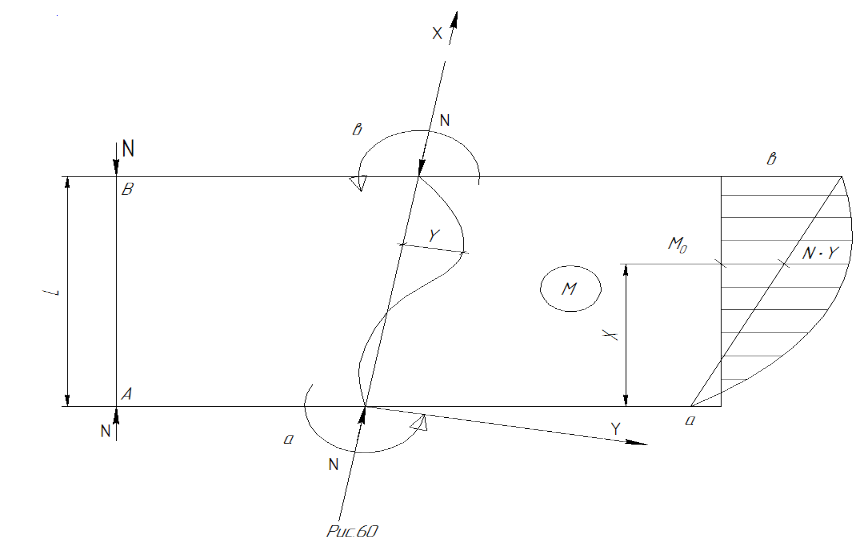
Рис.66 Произвольный участок AB стержня с приложенными по концам продольной силой N и моментами а и b
Так как 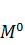 – линейная функция, то вторая производная от неё обратилась в нуль.
– линейная функция, то вторая производная от неё обратилась в нуль.
Учитывая, что 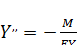 и
и 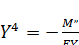 , имеем:
, имеем: 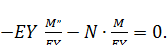 (125)
(125)
Обозначив 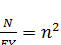 , получим следующее дифференциальное уравнение:
, получим следующее дифференциальное уравнение:
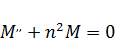 (126)
(126)
Решение этого дифференциального уравнения известно:
 (127)
(127)
Из граничных условий 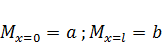
Найдем 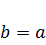 ;
; 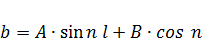
или 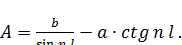
Уравнение (127) запишется так:
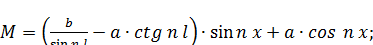 (128)
(128)
Эпюра моментов 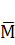 от единичного воздействия всегда будет прямолинейной (рис.67) и момент в произвольном сечении может быть предоставлен уравнением:
от единичного воздействия всегда будет прямолинейной (рис.67) и момент в произвольном сечении может быть предоставлен уравнением:
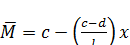 . (129)
. (129)
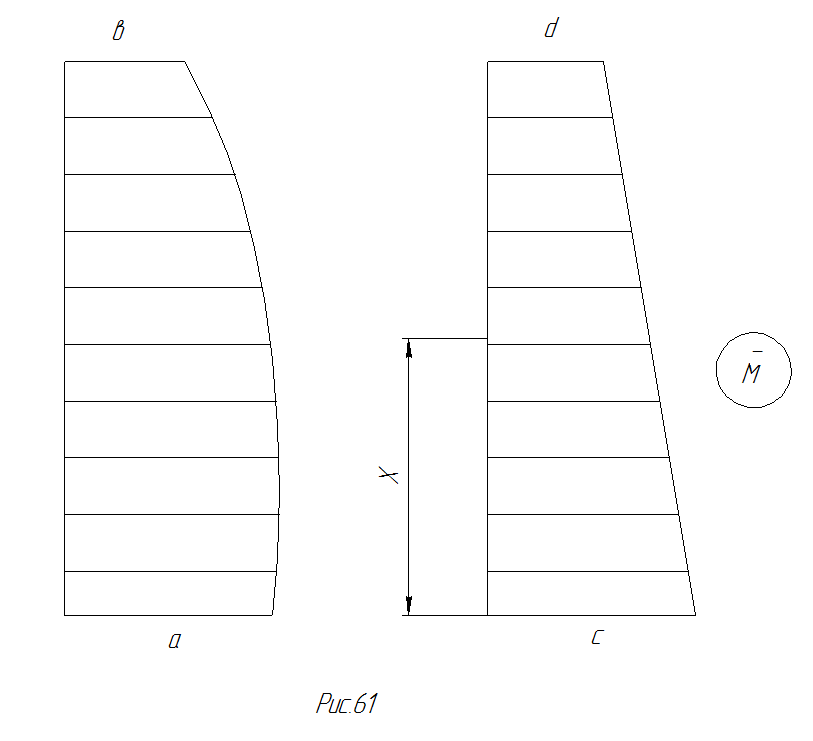
Рис. 67 Эпюры моментов М от единичных воздействий
Подставим полученные значения М и 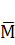 в интеграл:
в интеграл: 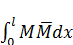 .
.
После интегрирования, приведения подобных членов и введения нового обозначения
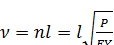 (130)
(130)
получим формулу, которую будем называть «обобщённой формулой трапеции»:
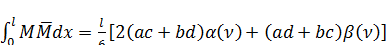 , (131)
, (131)
где  ;
;
 .
.
Коэффициенты 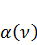 и β(
и β(  ), вычисленные в зависимости от
), вычисленные в зависимости от 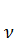 , приведены в таблице 2.(Приложение см.)
, приведены в таблице 2.(Приложение см.)
Формула (131) устанавливает правило определения перемещений путём «перемножения» двух эпюр. Перемножаются только трапеции эпюр моментов М и 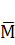 от поперечной нагрузки без учёта действия продольной силы, влияние которой учитывается множителями
от поперечной нагрузки без учёта действия продольной силы, влияние которой учитывается множителями 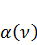 и β(
и β(  ).
).
Заметим, что при 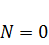 ;
; 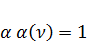 , β(
, β(  )=1и «обобщённая формула трапеции» совпадает с обычной «формулой» трапеции для перемножения двух линейных эпюр.
)=1и «обобщённая формула трапеции» совпадает с обычной «формулой» трапеции для перемножения двух линейных эпюр.
Если участок имеет переменные по его длине момент инерции и нормальную силу, то его необходимо разбить на конечное число малых участков и рассматривать EY и N для малого участка приближенно постоянными.
Пример. Дана «сжато-изогнутая» система, показанная на рисунке 68.
Требуется определить углы  и β с учётом продольного изгиба.
и β с учётом продольного изгиба.
Воспользуемся «обобщённой формулой трапеции» (131).
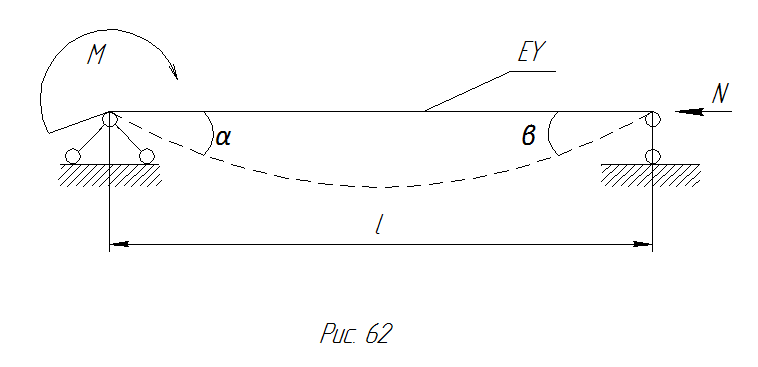
Рис. 68 Расчетная схема «сжато-изогнутой» балки
Действительная эпюра моментов М и две единичных эпюры моментов, соответствующие девиациям  и β, показаны на рис. 69.
и β, показаны на рис. 69.
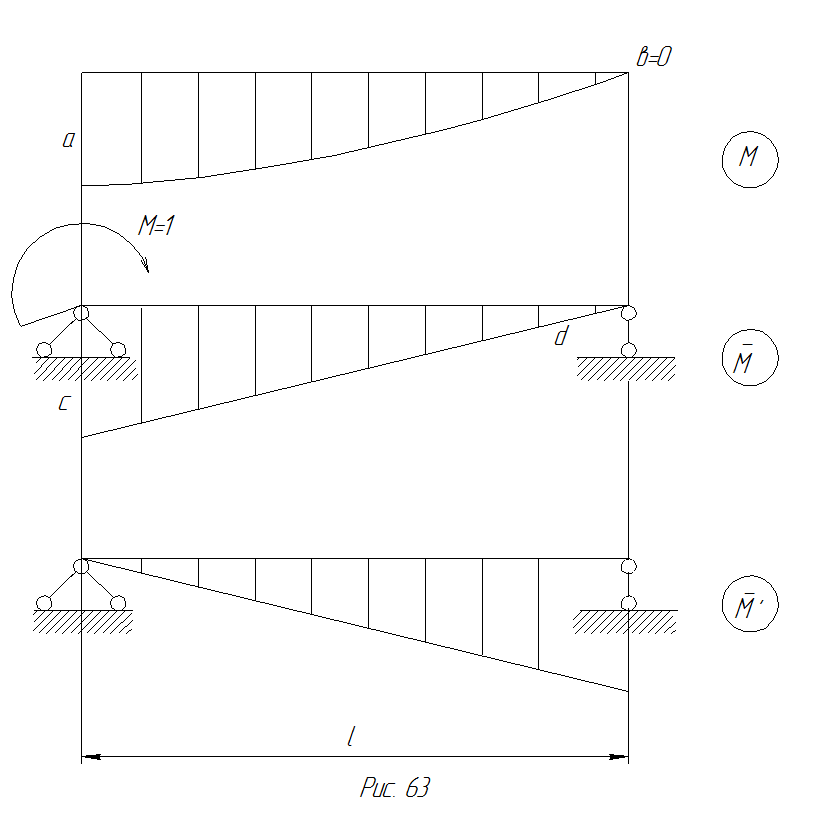
Рис. 69 Действительная эпюра моментов М и две единичных эпюры моментов
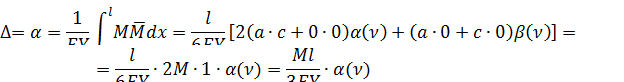
Если N=0, то 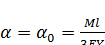 при
при 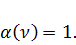
Следовательно, 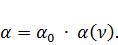
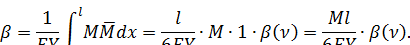
Так как 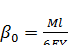 , то
, то 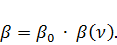
| <== предыдущая лекция | | | следующая лекция ==> |
| Устойчивость оболочек и пластин в пределах упругости | | | ОСНОВНЫЕ ТИПЫ КРИСТАЛЛИЧЕСКИХ РЕШЕТОК |
Дата добавления: 2017-01-26; просмотров: 1183;










