Понятие выборки. Построение по выборке графиков
Пусть требуется изучить некоторую совокупность однородных объектов.
Назовём множество всех изучаемых объектов генеральной совокупностью. Выборочной совокупностью, или кратко выборкой, назовём объекты, отобранные для исследования из генеральной совокупности, а их число n -объёмом выборки.
Для того чтобы по данным выборки можно было достаточно уверенно судить об интересующем нас признаке генеральной совокупности, необходимо, чтобы объем выборки был достаточно велик и выборка должна достаточно хорошо представлять пропорции генеральной совокупности. Кратко это требование звучит так: выборка должна быть репрезентативной (представительной), для чего каждый из её объектов должен быть отобран из генеральной совокупности случайным образом, то есть все объекты генеральной совокупности должны иметь одинаковую вероятность попасть в выборку.
К чему может привести несоблюдение правила случайного отбора, показывают многочисленные случаи неправильного проведения предвыборных опросов. Например, в 1936 году перед президентскими выборами в США журнал “Literary Digest” провел опрос 10 миллионов избирателей и предсказал, что Франклин Рузвельт проиграет выборы. Фамилии опрашиваемых избирателей были взяты из телефонных книг. Но в годы депрессии люди, имевшие телефон, не представляли всех избирателей США, выборка оказалась нерепрезентативной и прогноз не оправдался.
Существуют специальные приёмы отбора, обеспечивающие репрезентативность выборки, описание которых можно найти в книгах по статистике. Мы же будем в дальнейшем предполагать, что это требование выполнено и будем обсуждать только вопросы обработки выборочных данных.
Пусть из генеральной совокупности извлечена выборка объёмом n. Случайный выбор элемента рассматривается как независимое наблюдение над величиной x, имеющей некоторое распределение вероятностей. Те значения y1, y2…yn, которые приняла случайная величина x в n наблюдениях, называются ее реализациями. Если эти числа записать не в порядке получения, а в порядке возрастания, то получим упорядоченную выборку x1,x2,…xn, называемую вариационным рядом. Расстояние xn-x1между крайними членами ряда называется размахом вариационного ряда. Выборка и вариационный ряд несут практически одну и ту же информацию, но с вариационным рядом легче работать в силу его упорядоченности. Если изучается величина, имеющая непрерывное распределение вероятностей, то, скорее всего, вариационный ряд не будет содержать повторяющихся значений. Если же изучается дискретная случайная величина, то при достаточно большом объеме выборки в выборке будут повторяющиеся значения. Назовем относительной (эмпирической) частотой значения xiчастоту mi/n, где mi– число совподающих элементов xiв выборке объема n. Разные значения xiназовем вариантами.
Построим по выборке таблицу из двух строк: в верхней строке указаны в порядке возрастания наблюдаемые значения, а в нижней – соответствующие им относительные частоты. Эта таблица называется таблицей статистического распределения выборки.
Для выборки из непрерывного распределения (нет повторяющихся значений) эта таблица будет иметь вид
| Значения xi | x1 | x2 | … | xn |
| Частоты mi/n | 1/n | 1/n | … | 1/n |
Для выборки с повторяющимися значениями таблица выглядит так:
| Значения xi | x1 | x2 | … | xk |
| Частоты mi/n | 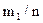
| 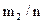
| … | 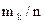
|
Соответствие между вариантами, записанными в порядке возрастания, и относительными частотами, задаваемоетаблицей статистического распределения выборки, называется статистическим (или эмпирическим) распределением выборки.
Пример . Имея конкретную выборку: 2, 6, 12, 6, 6, 2, 6, 12, 12, 6, 6, 6, 12, 12, 6, 12, 2, 6, 12, 6 (n=20), записать вариационный ряд и дать таблицу статистического распределения выборки.
Решение. Вариационный ряд: 2, 2, 2, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 12, 12, 12, 12, 12, 12, 12.
Статистическое распределение выборки:
| Варианты | |||
| mi | |||
| Частоты mi/n | 0,15 | 0,5 | 0,35 |
Контроль: 0,15 + 0,5 + 0,35=1.
При большом числе наблюдений над непрерывной случайной величиной обычно прибегают к группировке данных: область на оси x, куда попали значения x1,…,xn, разбивают на 5-15 интервалов I1, I2,…,Iк (причем длины интервалов не обязательно одинаковы). В качестве “принимаемого” значения при этом будут выступать середины интервалов. Примером самого простого вида группировки может служить округление выборочных значений до ближайшего целого числа. Например, последовательность 0,414, -0,011, 0,666, -1,132 и т.д. обращается в 0, 0, 1, -1,… Аналогично округление может производиться до ближайшего числа, кратного 10 или 100.
Пусть mj- число наблюдений, попавших в интервал Ij, к - число интервалов.
Тогда
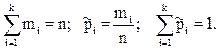 (3.1)
(3.1)
Для наглядного представления статистического распределения пользуются графическим изображением вариационных рядов (полигоном, гистограммой и кумулятой).
В случае дискретного распределения на оси абсцисс откладывают отдельные наблюденные значение х1. Из этих точек хiвосставим перпендикуляры к оси ОХ длиной 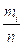 либо просто mi. Соединяя отрезками верхние концы соседних перпендикуляров, получим ломаную, называемую полигоном.
либо просто mi. Соединяя отрезками верхние концы соседних перпендикуляров, получим ломаную, называемую полигоном.
Гистограммастроится только для интервального вариационного ряда (группированной выборки). На каждом из интервалов значений как на основании строят прямоугольник с высотой, пропорциональной mi- числу точек выборки в интервале Ii. Если середины верхних сторон соседних прямоугольников соединить отрезками прямых и концы этой ломаной еще соединить с серединами соседних интервалов, частоты которых равны 0, а длина равна длине ближайшего интервала, то получим полигон для группированной выборки.
По выборке легко получить эмпирическуюфункцию распределения (или функцию распределения выборки, или накопленные частоты). Пусть х - точка оси ОХ, а nx- число точек выборки, попавших левее точки х. Тогда 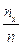 - доля точек выборки, лежащих левее точки х. Эта частота зависит от х и представляет собой эмпирическую функцию распределения
- доля точек выборки, лежащих левее точки х. Эта частота зависит от х и представляет собой эмпирическую функцию распределения 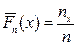 . Её график - ступенчатая линия. Сглаженное графическое представление этой функции для непрерывной случайной величин даёт кумулята. Покажем это для группированных данных. Имея интервалы группировки I1, I2,...,Ik, подсчитываем в правом конце каждого интервала накопленную частоту и строим перпендикуляр к оси ОХ высотой
. Её график - ступенчатая линия. Сглаженное графическое представление этой функции для непрерывной случайной величин даёт кумулята. Покажем это для группированных данных. Имея интервалы группировки I1, I2,...,Ik, подсчитываем в правом конце каждого интервала накопленную частоту и строим перпендикуляр к оси ОХ высотой 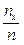 (либо проста высотой nx). Соединяя отрезками прямой верхние концы соседних перпендикуляров, получаем ломаную -кумуляту. Она монотонно поднимается от 0 до 1.
(либо проста высотой nx). Соединяя отрезками прямой верхние концы соседних перпендикуляров, получаем ломаную -кумуляту. Она монотонно поднимается от 0 до 1.
Проще всего показать на конкретном примере, как строятся эти графики (рис. 3.1, 3.2).
Таблица распределения продавцов по выработке
| Выработка продавцов | Число продавцов | В процентах к итогу | Кумулятивная (накопленная) численность | Накопленная частота |
| 80-100 | 0.1 | |||
| 100-120 | 15(5+10) | 0.3 | ||
| 120-140 | 35(15+20) | 0.7 | ||
| 140-160 | 45(35+10) | 0.9 | ||
| 160-180 | 50(45+5) | |||
| И т о г о |
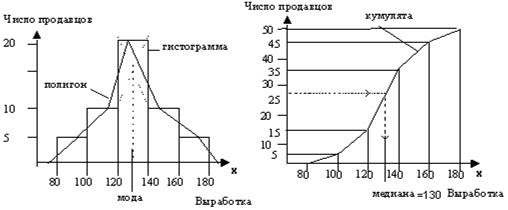
Рис. 3.1 Рис. 3.2
На оси Y могут откладываться не количества, а проценты или проценты, деленные на константу, например частоты. Вид графика от этого не изменится (рис. 3.3, 3.4).
В нашем примере длины интервалов одинаковы. В этом случае при построении гистограммы можно изображать прямоугольники высоты mi. Если длины интервалов разные, то при построении гистограммы это надо учитывать. Например, все интервалы имеют длину 10, кроме крайнего, который имеет длину 50 (весь “хвост” объединен в один интервал). Все попавшие в него данные можно мысленно разбить на 5 одинаковых частей, каждая из которых попала бы в свой интервал длины 10. Следовательно, высота прямоугольника над этим интервалом длины 50 должна браться в 5 раз меньше, чем его m.
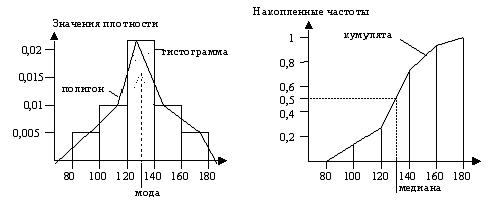
Рис. 3.3 Рис. 3.4
Если строить прямоугольники высоты mi/din, где di– длина интервала Ii, то гистограмма будет изображать эмпирическую плотность. Действительно, плотность вероятности – это вероятность, “приходящаяся в данной точке на единицу измерения”. Вероятность попасть в i-й интервал равна mi/n. Если di- это длина i-го интервала, то вероятность, приходящаяся на единицу измерения, которая и является значением эмпирической плотности внутри этого интервала, равна mi/din (в этом случае вероятность попадания в i-й интервал будет 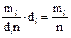 ). Если строить прямоугольники с такими высотами, то суммарная площадь всех прямоугольников будет равна 1. Таким образом, в случае, когда длины всех интервалов одинаковые, при построении гистограммы по оси y можно откладывать просто значения mi. Если длины интервалов разные, то надо брать за основу mi/di– количества, приходящиеся в этом интервале на единицу интервала. Если высоты прямоугольников сделать равными mi/din, то гистограмма изображает эмпирическую плотность. Такая гистограмма самая удобная в том смысле, что позволяет сравнивать два распределения, имеющие разный объем, и не зависит от способа группировки данных.
). Если строить прямоугольники с такими высотами, то суммарная площадь всех прямоугольников будет равна 1. Таким образом, в случае, когда длины всех интервалов одинаковые, при построении гистограммы по оси y можно откладывать просто значения mi. Если длины интервалов разные, то надо брать за основу mi/di– количества, приходящиеся в этом интервале на единицу интервала. Если высоты прямоугольников сделать равными mi/din, то гистограмма изображает эмпирическую плотность. Такая гистограмма самая удобная в том смысле, что позволяет сравнивать два распределения, имеющие разный объем, и не зависит от способа группировки данных.
Для дискретного вариационного ряда легко находится xi, в котором miимеет наибольшее значение – это значение, частота которого максимальна. Это значение называется эмпирической модой. Для интервального ряда легко находится интервал, у которого miмаксимально. Мода находится внутри него. Для вычисления ее значения пользуются формулой линейной интерполяции. На рис. 3.1 и 3.3 показано, как ее искать графически.
“Накопленные частоты” – это и есть значения эмпирической функции распределения, а кумулята – ее сглаженное графическое изображение.
На графике кумуляты (см. рис. 3.2 и 3.4), или сглаженной эмпирической функции распределения, показана эмпирическая медиана. Медиана – важная характеристика распределения вероятностей. Это такая точка, что половина принимаемых значений лежит слева от нее, а половина справа (это середина распределения). Для дискретного вариационного ряда медиана d ищется по формуле
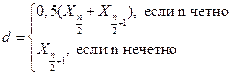 . (3.2)
. (3.2)
Для группированной выборки медиана – это точка, в которой площадь гистограммы делится пополам (в нашем примере – это такая выработка, что у 25 продавцов выработка меньше этого числа, а у 25 больше, и из соображений симметрии видно, что это 130). Если медиана лежит практически в центре области принимаемых значений, то это указывает на то, что у распределения нет сильного перекоса вправо или влево, например, оно симметрично относительно медианы. Сдвиг медианы влево (рис. 3.5) или вправо (рис. 3.7) от центра области принимаемых значений означает больший “вероятностный” удельный вес левой или, соответственно, правой половины распределения.
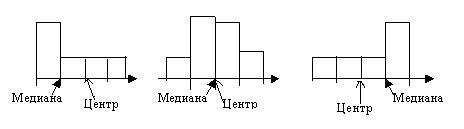
Рис. 3.5 Рис. 3.6 Рис. 3.7
Указав в качестве принимаемых значений середины интервалов группировки, мы строим вероятностную таблицу выборки.
| xi | mi | mi / n | Плотность вероятности | Накопленная частота (эмпирическая функция распределения) |
| 0,1 | 0,005 | 0,1 | ||
| 0,2 | 0,01 | 0,3 = (0,1 + 0,2) | ||
| 0,4 | 0,02 | 0,7 = (0,3 + 0,4) | ||
| 0,2 | 0,01 | 0,9 = (0,7 + 0,2) | ||
| 0,1 | 0,005 | 1 = (0,9 + 0,1) | ||
| n |
Итак, в самом общем случае по выборке построена таблица эмпирического распределения выборки.
Варианты 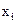
| 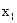
| 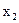
| … | 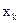
|
Частоты 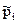
| 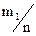
| 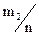
| … | 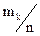
|
Далее задача заключается в том, чтобы по полученному экспериментальному материалу сделать выводы о виде распределения и получить оценки значений его числовых параметров.
Нетрудно заметить полную аналогию между статистическим распределением выборки и законом распределения дискретной случайной величины, но в данном случае вместо возможных значений случайной величины фигурируют варианты, а вместо соответствующих вероятностей – относительные частоты. В силу этой аналогии по известному эмпирическому распределению можно по тем же формулам, что и для дискретного распределения, найти выборочные аналоги математического ожидания и дисперсии или вычислить эмпирическую вероятность события (x<x) для любого x (она равна 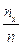 , где nx- число наблюдений xi, меньших х), т.е. найти эмпирическую функцию распределения (рис. 3.8), а гистограмму и полигон (рис. 3.9) можно рассматривать как эмпирическую плотность.
, где nx- число наблюдений xi, меньших х), т.е. найти эмпирическую функцию распределения (рис. 3.8), а гистограмму и полигон (рис. 3.9) можно рассматривать как эмпирическую плотность.
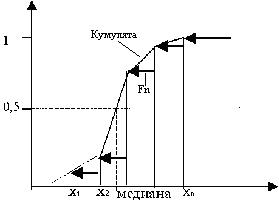
Рис. 3.8. Кумулята и эмпирическая функция распределения
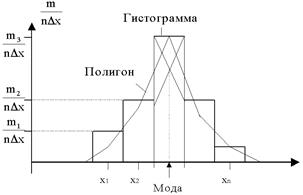
Рис. 3.9. Гистограмма и полигон
Если n увеличивать и, в случае группировки данных, длины интервалов группировки уменьшать, то гистограмма и полигон неограниченно приближаются (на каждом интервале сходятся по вероятности) к кривой плотности вероятности случайной величины (аналогично кумулята сходится по вероятности к теоретической функции распределения).
Поясним коротко, что означает термин “сходится по вероятности”. В курсе анализа изучалось понятие сходимости. Последовательность {an} называется сходящейся к a при n, стремящимся к бесконечности, если разность |an-a| становится при неограниченном росте n как угодно мала. Сходимость случайной величины по вероятности к некоторому значению означает, что, несмотря на увеличение числа испытаний, могут встретиться значения случайной величины, довольно сильно отличающиеся от предельного значения, но процент таких испытаний будет с ростом n уменьшаться (вероятность отклонения от предела стремится к 0). С такой сходимостью мы встречались выше, когда с помощью неравенства Чебышева оценивали вероятность отклонения случайной величины от своего математического ожидания более чем на e. Эта вероятность оценивается сверху с помощью дисперсии. Следовательно, последовательность случайных величин Х1, Х2,..., Хnс общим средним m = MXn = const, дисперсии DXnкоторых стремятся к нулю при n ® ¥, сходится по вероятности к числу m. Строгая запись такой сходимости 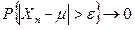 при
при 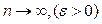 . С помощь этих рассуждений доказывается сходимость по вероятности многих случайных величин, встречающихся далее.
. С помощь этих рассуждений доказывается сходимость по вероятности многих случайных величин, встречающихся далее.
По виду построенной нами гистограммы (см. рис. 3.9) можно предположить, что она построена по выборке из нормального распределения.
Приведенная ниже гистограмма (рис. 3.10) дает основание полагать, что выборка получена из равномерного распределения, график плотности вероятности которого имеет вид прямоугольника, т.е. задается отрезком прямой, параллельной оси ОХ.
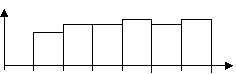
Рис. 3.10
Еще одна гистограмма (рис. 3.11) – не из нормального и не из равномерного распределения.
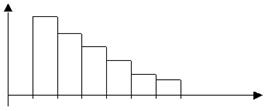
Рис. 3.11
Эти примеры демонстрируют, как по гистограмме, построенной по выборке, можно оценить вид распределения вероятностей.
В дальнейших рассуждениях мы ограничимся рассмотрением случая, когда известен вид теоретического распределения, но неизвестны и подлежат определению параметры распределения. Так, в разделе 2.4 с помощью теоремы Муавра-Лапласа для биномиального распределения мы по результатам n раз проведенного эксперимента оценивали значение p. Теперь будем решать похожую задачу: известно, что интересующая нас величина распределена нормально, над ней n раз проводятся испытания; необходимо оценить по результатам испытаний ее математическое ожидание и среднеквадратическое отклонение (или дисперсию). Эта задача охватывает очень большой круг приложений ввиду того, что нормальное распределение является одним из самых распространенных распределений вероятности, так как согласно центральной предельной теореме такое распределение или близкое к нему имеют случайные величины, являющиеся суммой большого числа независимых взаимодействий. Эта же методика позволяет решить задачу сравнения двух выборок и ряд других задач.
3.2. Построение точечных оценок с помощью метода моментов.
Вычисление эмпирических моментов
Предположим, что заранее известен вид теоретического распределения интересующего нас признака x, но параметры этого распределения не известны и их желательно найти как можно точнее по данным выборки.
Для решения задачи оценивания параметров теоретического распределения нам понадобится строить функции, зависящие от выборочных значений x1,..., xn. Любую функцию q(x1, ..., xn), зависящую от выборки и поэтому являющуюся случайной величиной, принято называть статистикой. Так, 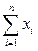 -сумма наблюдений и среднее арифметическое значение
-сумма наблюдений и среднее арифметическое значение 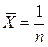
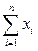 служат примерами статистик. Чтобы оценки неизвестных параметров, то есть статистики, давали хорошее приближение неизвестных параметров распределения генеральной совокупности, они должны удовлетворять следующим требованиям:
служат примерами статистик. Чтобы оценки неизвестных параметров, то есть статистики, давали хорошее приближение неизвестных параметров распределения генеральной совокупности, они должны удовлетворять следующим требованиям:
- среднее значение оценки, взятое по всевозможным выборкам данного объёма, должно равняться истинному значению определяемого параметра; в этом случае оценку называют несмещённой;
- при увеличении объёма выборки оценка должна сходиться по вероятности к истинному значению параметра; в этом случае оценку называют состоятельной.
По выборке мы вычислим либо точечнуюоценку (значение подходящей статистики) для интересующего нас параметра, либо интервальную(т.е. интервал, с большой вероятностью накрывающий истинное значение параметра).
Очень часто параметры распределения вероятностей являются моментами распределения (или функциями от них). Например, нормальное распределение полностью определяется математическим ожиданием и дисперсией. Математическое ожидание является первым начальным моментом, а дисперсия – вторым центральным моментом распределения. Так что очень важно научиться строить оценки именно для моментов.
Начальный момент l-го порядка распределения вероятностей alнаходится по формулам:
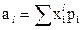 - для дискретного распределения;
- для дискретного распределения;
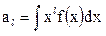 - для непрерывного распределения.
- для непрерывного распределения.
А l-й центральный момент blпо формулам:
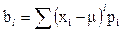 - для дискретного распределения;
- для дискретного распределения;
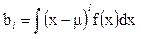 - для непрерывного распределения,
- для непрерывного распределения,
где m - математическое ожидание распределения, т.е. его первый начальный момент (суммирование выполняется по всем принимаемым значениям, интегрирование – по всей области определения).
Для построения точечных оценок для математического ожидания и дисперсии генеральной совокупности или любых других моментов сделаем очень простую вещь. Таблица статистического распределения выборки задает некоторое распределение вероятностей, а именно, распределение выборки. Представим себе, что все числа, полученные с помощью выборки, мы сложили в урну. Согласно классической схеме, если доставать случайным образом из урны числа, то вероятность р1достать число х1равна m1/n , вероятность р2достать число х2равна m2/n и так далее. То есть таблица статистического распределения действительно задает распределение выборки. Среднее, вычисленное для выборки по таблице статистического распределения, назовем эмпирическим средним.Его и возьмем в качестве оценки для математического ожидания генеральной совокупности. Дисперсию этого распределения назовем эмпирической дисперсиейи ее возьмем в качестве оценки для дисперсии генеральной совокупности. Так же можно сосчитать и любые другие эмпирические моменты.
Выбирая оценками такие статистики, мы воспользовались методикой, предлагаемой методом моментов. Так называется метод, при котором в качестве оценок для моментов распределения берутся эмпирические моменты (или моменты эмпирического распределения). Его применяют в тех случаях, когда оцениваемый параметр интересующего нас распределения является функцией от моментов распределения. Тогда в эту функцию вместо неизвестных теоретических значений моментов подставляют эмпирические значения. Например, в нашем случае оцениваемые параметры сами являются моментами. Математическое ожидание – первый начальный, а дисперсия – второй центральный момент. В качестве оценок для них мы и берем первый начальный и второй центральные моменты выборки. Аналогично по выборке строятся эмпирические оценки для функций моментов более высокого порядка: асимметрии – третьего центрального момента, деленного на среднеквадратическое отклонение в третьей степени, и эксцесса – четвертого центрального момента, деленного на квадрат дисперсии.
Итак, по выборке мы построили эмпирическое распределение, затем по нему сосчитаем эмпирическое среднее и эмпирическую дисперсию и другие моменты. Вспомним формулы для вычисления математического ожидания и дисперсии и других моментов по таблице дискретного распределения и применим их к построенной по выборке таблице статистического распределения.
Вычисление эмпирических моментов по вариационному ряду производится по следующим формулам (во всех формулах n - объем выборки):
начальный эмпирический момент l-го порядка
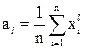 ; (3.3)
; (3.3)
центральный эмпирический момент l-го порядка
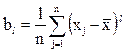 . (3.4)
. (3.4)
В случае, когда применяется группировка данных или просто одно и то же значение xiв обрабатываемой последовательности повторяется miраз (задана таблица распределения), эти формулы приобретают следующий вид:
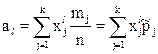 (3.5)
(3.5)
и
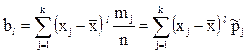 , (3.6)
, (3.6)
где k – число разных значений вариант или, в случае группировки, интервалов.
Если формулу 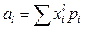 , применяемую для вычисления начального момента l-го порядка дискретной случайной величины, применить к эмпирическому распределению (когда в роли
, применяемую для вычисления начального момента l-го порядка дискретной случайной величины, применить к эмпирическому распределению (когда в роли 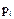 выступают
выступают 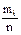 ), то получим формулу (3.5), или, что то же, (3.3). В частности,
), то получим формулу (3.5), или, что то же, (3.3). В частности, 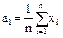 - выборочное среднее. Обычно его обозначают
- выборочное среднее. Обычно его обозначают 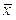 . Итак,
. Итак,
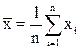 (3.7)
(3.7)
для выборки, заданной вариационным рядом, и
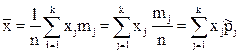 (3.7а)
(3.7а)
для выборки, заданной таблицей.
Выборочную дисперсию 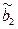 обычно обозначают S2.
обычно обозначают S2.
В силу того, что верно тождество
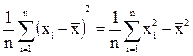 ,
,
для вычисления S2получаем формулу
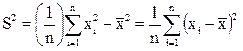 (3.8)
(3.8)
для выборки, заданной вариационным рядом, и
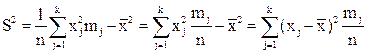 (3.8а)
(3.8а)
для выборки, заданной таблицей.
В отличие от МХ и DX, величины 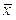 и S3случайные.
и S3случайные.
Пример. По выборке 4, 6, 7, 7, 10, 15, 18 (n=7) найти 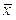 и S2.
и S2.
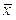 =(4+6+7+7+10+15+18)/7=9,57.
=(4+6+7+7+10+15+18)/7=9,57.
S2=1/7(16+36+49+49+100+225+324)-(9,57)2=114,14-91,58=22,56.
Пример. Найти 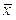 и S2по таблице
и S2по таблице
| Варианты | ||||
| mi | n=20 |
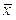 =(2×3+6×10+12×7)/20=7,5.
=(2×3+6×10+12×7)/20=7,5.
S2=1/20(4×3+36×10+144×49)-(7,5)2=(1/20)×7428-56,25 = 371,4-56,25=315,15.
Запомним: согласно методу моментов точечной оценкой для математического ожидания надо взять 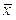 , оценкой для дисперсии - S2.
, оценкой для дисперсии - S2.
Дата добавления: 2017-01-08; просмотров: 7340;










