Нормальное распределение

Нормальное распределение - распределение Гаусса играет особую роль в теории вероятностей и её приложениях. Это наиболее часто встречающийся на практике закон распределения. Этому закону подчиняется, при соблюдении определённых условий, распределение суммы достаточно большого числа случайных величин, каждая из которых может иметь произвольное распределение. Так, при изучении биномиального распределения мы воспользовались тем, что число появлений события A в схеме Бернулли можно представить в виде суммы индикаторов. Пользуясь этим, можно показать, что при n ® ¥ биномиальное распределение быстро приближается к нормальному, в чем и состоит интегральная теорема Муавра-Лапласа.

Непрерывная случайная величина распределена нормально, если её плотность вероятности имеет вид

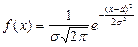. (2.21)

Графики плотности вероятности и функции распределения приведены ниже (рис. 2.4).

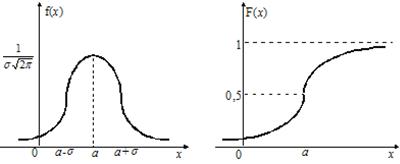
Рис. 2.4

График плотности вероятности симметричен относительно прямой x=a, максимальное значение равно 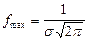и достигается при x = a. Условие нормировки (2.5) выполняется.

Параметрами, определяющими нормальное распределение (иногда употребляется запись N(a,s)), являются a - математическое ожидание и s - среднеквадратическое отклонение.

Очевидно, изменение параметра a сводится к сдвигу графика f(x) по оси OX. Чтобы понять, как влияет параметр s на этот график, заметим, что при уменьшении s возрастает fmax. Но площадь фигуры, ограниченная графиком плотности вероятностей и осью OX, равна 1, поэтому при уменьшении s кривая должна быстрее приближаться к оси OX вдали от x = a и более резко возрастать вблизи этого значения.

Величину x~N(0,1) с нулевым средним и единичным среднеквадратическим отклонением называют стандартной нормальной. Ее плотность вероятности и функция распределения задаются формулами:

.

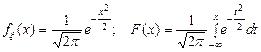Интеграл функции распределения не выражается через элементарные функции, но в виду его важности для него есть таблицы. Пользуясь таблицами, надо быть внимательным, так как часто через F(x) обозначают (и задают таблицы для этой функции) интеграл, у которого нижний предел равен –x, или 0 (функция Лапласа F(x), см. табл. 4 приложения). В силу симметрии f(x) относительно нуля достаточно задавать значения F(x) и F(x) только для положительных x. Легко видеть, что все три функции связаны простыми соотношениями, позволяющими по любой из них вычислить значения двух других. Действительно, в силу известного из курса анализа соотношения 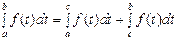и симметричности f(x) относительно нуля,

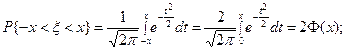
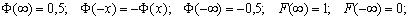
F(х)=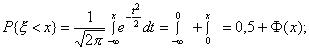

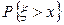
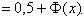
Как для x~N(0,1), так и для h~N(a,s), вероятность попадания в любой интервал может быть выражена через F(x), то есть вычислена с помощью таблиц. Покажем это:

;

(*)

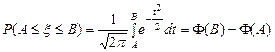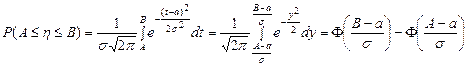(мы сделали замену переменных ).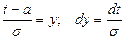

Воспользуемся полученным соотношением и получим так называемое правило трёх s. Для этого найдём

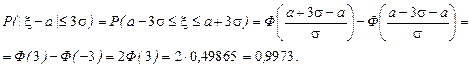
То есть практически достоверно то, что нормально распределённая величина примет значение, отличающееся от её среднего по модулю не более чем на 3s, иначе говоря, практически невозможно появление значения, выходящего за пределы этого интервала. Последнее обстоятельство находит широкое применение в различных приложениях.

Аналогичным образом можно найти вероятности:

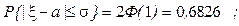
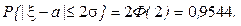
Пример. Затаривание мешков с сахаром производится без систематических ошибок. Случайные ошибки подчинены нормальному закону со среднеквадратическим отклонением
s = 200 г. Найти вероятность того, что затаривание будет проведено с ошибкой, не превосходящей по абсолютной величине 100 г.

Решение. В задаче рассматривается случайная величина - ошибка взвешивания, то есть разность (h - a) между случайным значением веса мешка сахара и его нормативным значением a- математическим ожиданием. Требуется найти

.

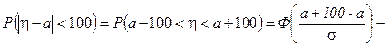
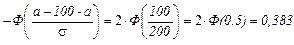Здесь мы применили формулу (*) с s = 200 и таблицу 4 .

Отметим очень важное свойство нормального распределения– его воспроизводимость: сумма (разность) независимых нормальных величин является нормальной величиной.

Предельные теоремы

Сейчас нас будут интересовать закон распределения и некоторые связанные с ним числовые характеристики суммы случайных величин при условии, что распределение и числовые характеристики слагаемых известны, а их число неограниченно возрастает.

Неравенство Чебышева (приводится без доказательства). Для произвольной случайной величины x с математическим ожиданием a = M(x )и дисперсией s 2= D(x )для любого e > 0 справедливо неравенство

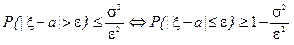. (2.22)

Из неравенства Чебышева следует: чем меньше дисперсия, тем меньше вероятность отклонения случайной величины от своего математического ожидания более чем на e.

Теорема Чебышева(приводится без доказательства). Пусть {xn} - последовательность независимых одинаково распределенных случайных величин, имеющих конечные дисперсии. Тогда вероятность отклонения их среднего арифметического от их математического ожидания по модулю меньше чем на e стремится к 1 при неограниченном увеличении n.

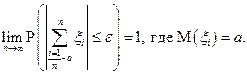(2.23)

В этом случае говорят, что среднее арифметическое случайных величин сходится по вероятности к среднему арифметическому математических ожиданий слагаемых.

Пример. Обычно при определении численного значения некоторой постоянной величины проводится несколько измерений и в качестве искомого значения принимается их среднее арифметическое. Действительно, результат каждого измерения можно рассматривать как случайные величины x1, ..., xn. Если результаты измерений независимы, имеют одно и то же математическое ожидание и их дисперсии ограничены одной и той же константой (что на практике обычно выполняется), то согласно теореме Чебышева среднее арифметическое 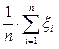сходится по вероятности к 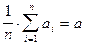(истинному значению измеряемой величины).

Теорема Бернулли (следствие теоремы Чебышева).Эта теорема устанавливает связь между относительной частотой события n(A) и его вероятностью p(A). Пусть производится n независимых, однородных испытаний (схема Бернулли), в каждом из которых событие А может произойти с вероятностью p(A)=р. Введём в рассмотрение случайные величины x₁, ... , x_n- индикаторы испытаний. Напомним, что x_iпринимает только два значения: a) 1, если в i -м испытании событие A наступило, b) 0 в противоположном случае. Ранее были найдены M(x_i) = p и D(x_i) = pq. Последовательность случайных величин {x_i} удовлетворяет условиям теоремы Чебышева и поэтому

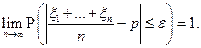
Остаётся отметить, что сумма 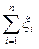равна числу появлений события A при n испытаниях, а значит, 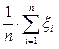является относительной частотой, которую ранее обозначали через n(A).

Таким образом, при неограниченном увеличении числа испытаний относительная частота n(A) события A сходится по вероятности к P(A) - вероятности его появления при одном испытании. Это утверждение и является теоремой Бернулли.