Теоретические законы распределения отказов, модели безотказности
В теории надежности используют различные математические модели появления отказов согласно природе их возникновения в зависимости от периода и условий эксплуатации или изготовления конструкции технических средств.
Интенсивность отказов технических средств λ(t) в течение срока службы изменяется во времени, как показано на рис. 27.
Для начального периода времени (от t0 до t1) характерны ранние отказы вследствие дефектов материала или производственных дефектов. Контроль качества и испытания первых образцов обычно позволяют исключить многие изделия, не отвечающие техническим требованиям, и избежать тем самым большой интенсивности отказов в начальный период.
Второй отрезок кривой (от момента t1 до момента t2) изображает случайные отказы (или внезапные отказы), вызываемые неожиданным увеличением напряжения, предельно тяжелыми условиями работы при неблагоприятном сочетании нагрузок и т. д.
Отрезок кривой после точки t2 изображает износовые отказы (или постепенные отказы). Здесь интенсивность отказов возрастает по мере старения оборудования.
В некоторых случаях более удобно выбирать модель интенсивности отказов, а не распределение наработки до отказа. Поэтому целесообразно рассмотреть различные модели интенсивности отказов.
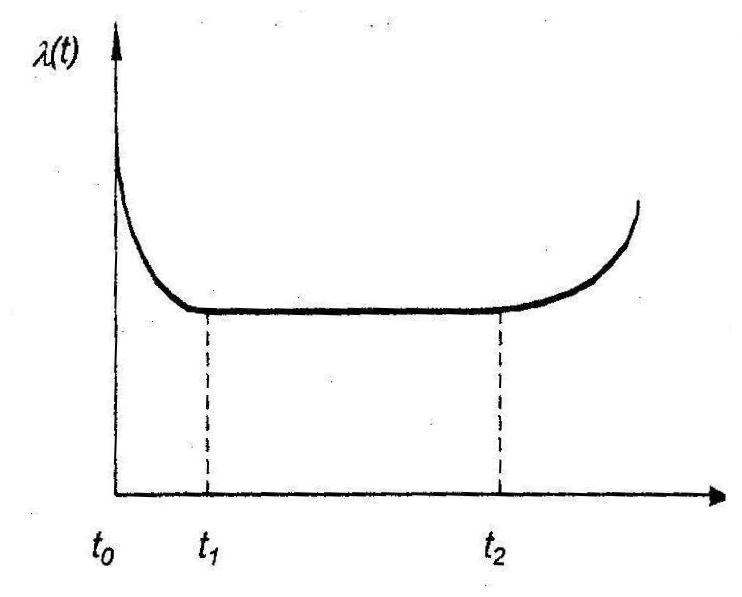
Рис.27. Интенсивность отказа за период службы изделия
Экспоненциальное распределение,
Рассмотрим вначале случаи внезапных отказов, когда постепенные отказы не оказывают значительного влияния (участок между t1 и t2 на рис. 27). В этих случаях в качестве вероятностной модели возникновения отказов используют экспоненциальное распределение, когда интенсивность отказов постоянная λ(t)=λ=const (Рис.28). Внезапные отказы не зависят от возраста деталей, и формула расчета вероятности безотказной работы имеет вид
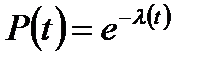
Плотность распределения
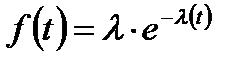
Как обычно λ(t) ≤ 0,1, поэтому формулу для вероятности безотказной работы можно упростить в результате разложения в ряд и отбрасывания малых членов:
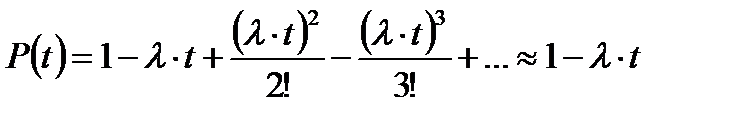
Интенсивность отказов в этом случае определяется выражением
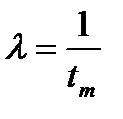
где 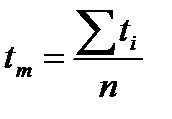 - средняя наработка до отказа; n - общее число отказов за наблюдаемый период.
- средняя наработка до отказа; n - общее число отказов за наблюдаемый период.
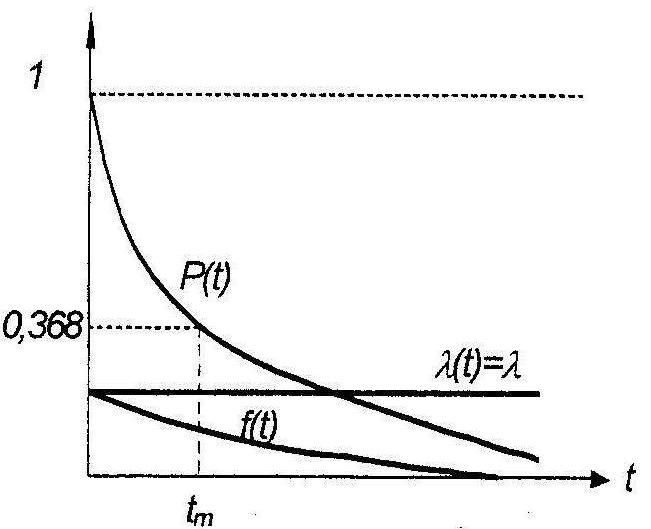
Рис. 28. Функции вероятности безотказной работы P(t), плотности вероятности f(t) и интенсивности отказов λ(t) экспоненционального распределения
Вероятность безотказной работы в зависимости от λ(t) t =t/tm
| λ(t) | 0,1 | 0,01 | 0,001 | 0,0001 | |
| P(t) | 0,368 | 0,9 | 0,99 | 0,999 | 0,9999 |
Вероятность P(t)=0,368 означает, что 62,2% отказов возникает за время t<tm , и только 36,8% позднее. Отсюда следует, что достижение требуемой вероятности безотказной работы 0,9 или 0,99 возможно при достачно малой доли среднего срока службы (соответственно 0,1 tm и 0,01 tm).
Закон нормального распределения
Для описания закона распределения времени безотказной работы в период появления постепенных (износовых) отказов наиболее универсальным, удобным и широко применяемым для практических расчетов является закон нормального распределения (участок после t2 на рис.27). Для постепенных отказов характерны законы распределения времени безотказной работы, которые вначале дают низкую плотность распределения, затем максимум и далее падение, связанное с уменьшением числа работоспособных изделий. График плотности вероятности нормального распределения в этом случае имеет колоколообразную форму, симметричную относительно среднего значения (Рис. 29).
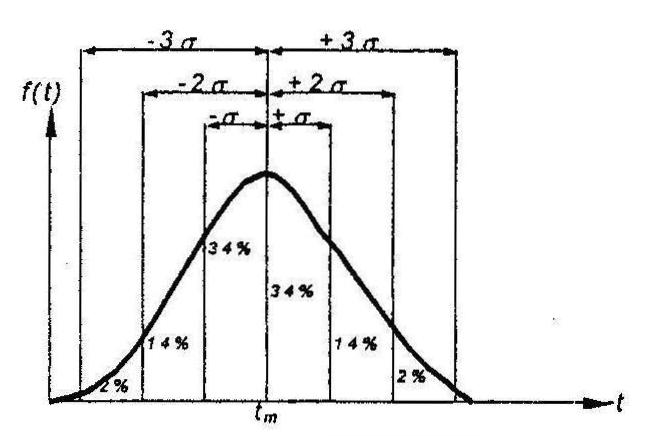
Рис.29. Функция плотности вероятности нормального распределения
В связи с многообразием причин и условий возникновения отказов в период нормального износа для описания надежности могут применяться различные законы распределения, которые устанавливают путем аппроксимации результатов испытаний и наблюдений в эксплуатации.
Нормальное распределение является наиболее универсальным, удобным и широко применяемым для практических расчетов. Распределение всегда подчиняется нормальному закону, если на изменение случайной величины оказывают влияние многие примерно равнозначные факторы. Этому закону подчиняется наработка до отказа большинства восстанавливаемых и невосстанавливаемых изделий, физико-механические свойства материалов изделий и сред взаимодействия, размеры и ошибки измерений деталей и т.д.
Плотность нормального распределения возникновения случайных событий-отказов описывается формулой Гаусса
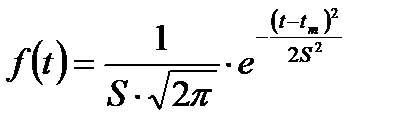
где t и tm текущая и средняя (математическое ожидание) наработ-
ки; 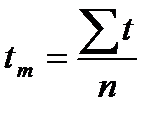 ; n - число изделии, вышедших из строя к заданному
; n - число изделии, вышедших из строя к заданному
моменту времени; е - основание натуральных логарифмов; S - среднее квадратическое отклонение от математического ожидания (tm) случайной величины (t) наработки на отказ
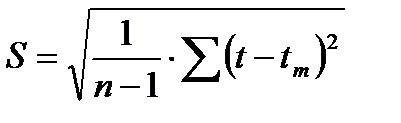
Иногда для характеристики изменчивости случайной величины используют дисперсию D=S2. Математическое ожидание tm на графике закона нормального распределения (см. рис.29) определяет положение вершины «колокола», а среднее квадратическое отклонение - ширину его основания.
Кривая плотности распределения нормального закона тем острее и выше, чем меньше S. Она начинается от t =-∞ и распространяется до t =+∞. Площадь, очерченная уходящими в бесконечность ветвями кривой плотности, выражающая соответствующую вероятность отказов, очень мала. Так, вероятность отказа за период времени до tm-3S составляет всего 0,135% и обычно в расчетах не учитывается. Вероятность отказа до tm-2S равна 2,175%. Наибольшая ордината кривой плотности распределения нормального закона равна
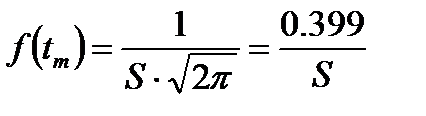
Вероятности отказа и безотказной работы взаимосвязаны
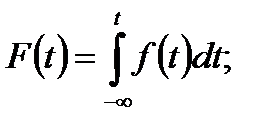
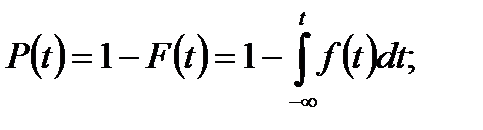
или
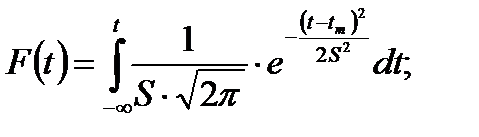
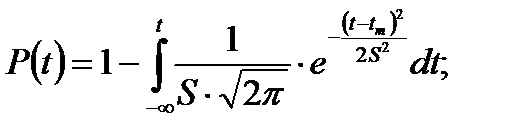
Вычисления интегралов заменяют таблицами. Однако таблицы для нормального распределения в функции двух переменных (t-tm) и S были бы громоздкими, поэтому пользуются небольшими таблицами в функции одной переменной х для нормального распределения, у которого mx=0 и Sx=1. Для этого распределения функция плотности имеет одну переменную х
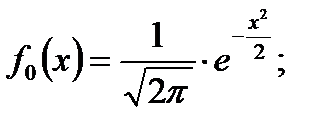
Величина х является центрированной, так как тх=0, и нормированной, так как Sx=1. Для использования таблиц определяют переменную х подстановкой 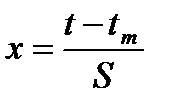 . В инженерной литературе эту переменную называют квантилью нормированного нормального распределения и обычно обозначают символом ир.
. В инженерной литературе эту переменную называют квантилью нормированного нормального распределения и обычно обозначают символом ир.
В литературе по надежности часто вместо интегральной функции распределения 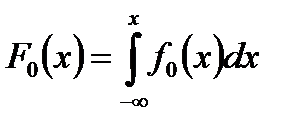 используют функцию Лапласа
используют функцию Лапласа
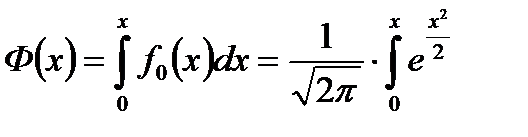
Тогда, учитывая, что
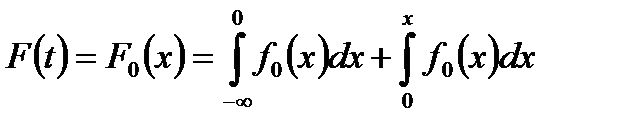 , а
, а 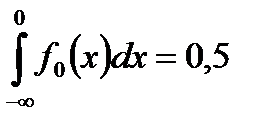
имеем
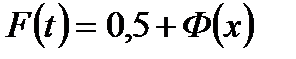
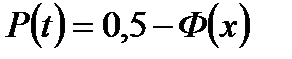
или же
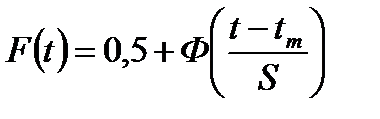
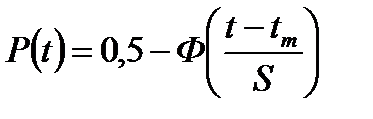
В результате полученные формулы позволяют определять вероятности событий в зависимости от квантилей нормального распределения
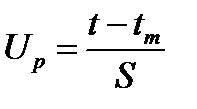
Помимо задачи оценки вероятности безотказной работы за данное время или за данную наработку часто возникает необходимость в решении обратной задачи - определение времени или наработки, соответствующих заданной вероятности безотказной работы. Значение этой наработки (времени) определяют с помощью квантилей нормированного нормального распределения
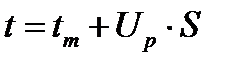
Значения квантилей даются в таблицах в зависимости от требуемой вероятности безотказной работы (табл.1). Операции с нормальным распределением проще, чем с другими, поэтому при малых значениях коэффициентов вариации V=S/tm, когда нормальное распределение хорошо заменяет другие распределения (пуассоново, логарифмически нормальное), отдают предпочтение нормальному распределению, и им заменяют другие распределения
Нормальное распределение Таблица 1.
| Квантиль Uр | Вероятность безотказной работы P(t) | Квантиль Uр | Вероятность безотказной работы P(t) |
| 0,5 | -1,751 | 0,96 | |
| -0,1 | 0,5398 | -1,8 | 0,9641 |
| -0,126 | 0,55 | -1,881 | 0,97 |
| -0,2 | 0,5793 | -2,0 | 0,9772 |
| -0,253 | 0,60 | -2,054 | 0,98 |
| -0,3 | 0,6179 | -2,1 | 0,9821 |
| -0,385 | 0,65 | -2,17 | 0,985 |
| -0,4 | 0,6554 | -2,2 | 0,9861 |
| -0,5 | 0,6915 | -2,3 | 0,9893 |
| -0,524 | 0,70 | -2,326 | 0,99 |
| -0,6 | 0,7257 | -2,4 | 0,9918 |
| -0,674 | 0,75 | -2,409 | 0,992 |
| -0,7 | 0,7580 | -2,5 | 0,9938 |
| -0,8 | 0,7881 | -2,576 | 0,995 |
| -0,842 | 0,8 | -2,6 | 0,9953 |
| -0,9 | 0,8159 | -2,652 | 0,996 |
| -1,0 | 0,8413 | -2,7 | 0,9965 |
| -1,036 | 0,85 | -2,748 | 0,397 |
Продолжение табл.1
| -1,1 | 0,8643 | -2,8 | 0,9974 |
| -1,2 | 0,8849 | -2,878 | 0,998 |
| -1,282 | 0,9 | -2,9 | 0,9981 |
| -1,3 | 0,9032 | -3,0 | 0,9986 |
| -1,4 | 0,9192 | -3,090 | 0,999 |
| -1,5 | 0,9332 | -3,291 | 0,9995 |
| -1,6 | 0,9452 | -3,5 | 0,9998 |
| -1,645 | 0,95 | -3,719 | 0,9999 |
| -1,7 | 0,9554 |
Распределение Вейбулла
Наиболее универсальной математической моделью описания распределения случайных величин является распределение Вейбулла, которое удовлетворительно описывает наработку деталей и элементов металлоконструкций по усталостным разрушениям. Распределение Вейбулла широко используется для оценки надежности деталей и узлов различных машин, в частности, автомобилей, подъемно- транспортных, землеройных и других машин.
Основные закономерности распределения Вейбулла:
вероятность безотказной работы
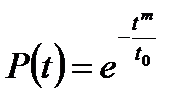
интенсивность отказов
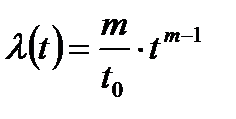
плотность распределения отказов
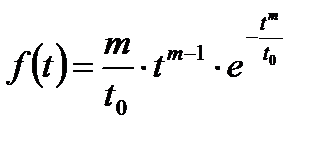
Здесь t0 характеризует масштаб кривой распределения и соответствует ее моде, т.е. время, при котором плотность вероятности максимальна. Показатель степени т определяет форму кривой плотности распределения.
Математическое ожидание и среднее квадратическое отклонение определяются соответственно формулами
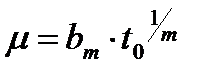
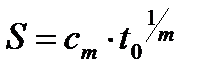
где bт и ст- коэффициенты, представленные в табл. 2 [1].
Рассмотрим частные случаи, характеризующие возможности и универсальность распределения Вейбулла:
т <1 - функции λ(t) и f(t) от наработки до отказа убывающие;
т=1 - распределение превращается в экспоненциальное λ(t)=const и f(t) - убывающая функция;
т> 1 - функция f(t) одновершинная, функция λ(t) непрерывно возрастающая при 1< m<2 с выпуклостью вверх, а при т>2 - с выпуклостью вниз;
т=2 - функция λ(t) является линейной и распределение Вейбулла превращается в распределение Рэлея;
m=3,3 - распределение Вейбулла близко к нормальному.
Эти свойства распределения Вейбулла используются при обработке результатов испытаний с целью установления закона распределения отказов технических изделий в процессе эксплуатации. Для этого выполняют следующие действия:
• составляют таблицу обработки результатов экспериментальных данных
| t | п | P(t) | y | lgy | lgt |
• по данным экспериментов определяют вероятность безотказной работы P(t)=1-n/N,
где N - общее количество изделий, принимавших участие в испытаниях на надежность, n - количество изделий, вышедших из строя к моменту времени t,
• определяют значение дополнительной функции y=-lgP(t);
для каждого момента t определяют lgy и lgt;в координатах lgt - lgy строят график (рис. 30), проводя через полученные точки прямую;
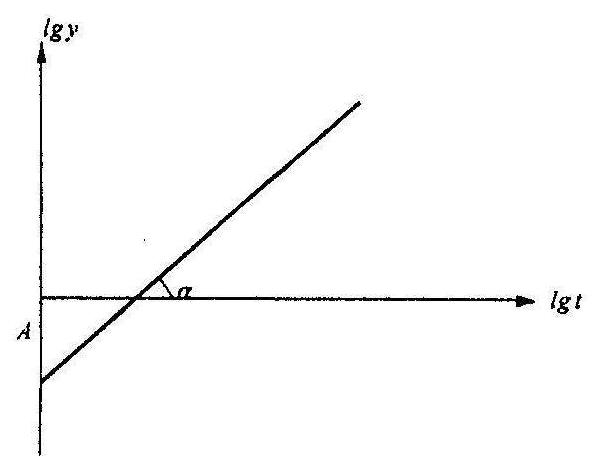
Рис.30. Графическое определение параметров распределение Вейбулла
• определяют значения показателя степени m=lgα и логарифма величины t0 lgt0=A-0,362, где α - угол наклона прямой к оси абсцисс, А - отрезок, отсекаемый прямой на оси координат;
• по полученному значению показателя степени т определяют закон распределения вероятности безотказной работы изделия.
Распределение Вейбулла Таблица 2
| Параметр формы т | 1/т | bт | cm | 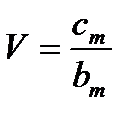
|
| 0,400 | 2,5 | 3,32 | 10,4 | 3,14 |
| 0,417 | 2,4 | 2,98 | 8,74 | 2,93 |
| 0,435 | 2,3 | 2,68 | 7,38 | 2,75 |
| 0,455 | 2,2 | 2,42 | 6,22 | 2,57 |
| 0,476 | 2,1 | 2.20 | 5.27 | 2.40 |
| 0,500 | 2,0 | 2,00 | 4,47 | 2,24 |
| 0,526 | 1,9 | 1,83 | 3,81 | 2,08 |
| 0,556 | 1,8 | 1,68 | 3,26 | 1,94 |
| 0,588 | 1,7 | 1,54 | 2,78 | 1,80 |
| 0,625 | 1,6 | 1,43 | 2,39 | 1,67 |
| 0,667 | 1,5 | 1,33 | 2,06 | 1,55 |
| 0,714 | 1,4 | 1,24 | 1,78 | 1,43 |
| 0,769 | 1,3 | 1,17 | 1,54 | 1,32 |
| 0,833 | 1,2 | 1,10 | 1,33 | 1,21 |
| 0,909 | 1,1 | 1,05 | 1,15 | 1,10 |
| 1,0 | 1,00 | 1,00 | 1,00 | 1,00 |
| 1,1 | 0,909 | 0,965 | 0,878 | 0,910 |
| 1,2 | 0,833 | 0,941 | 0,787 | 0,837 |
| 1,3 | 0,769 | 0,924 | 0,716 | 0,775 |
| 1,4 | 0,714 | 0,911 | 0,659 | 0,723 |
| 1,5 | 0,667 | 0,903 | 0,615 | 0,681 |
| 1,6 | 0,625 | 0,897 | 0,574 | 0,640 |
| 1,7 | 0,588 | 0,892 | 0,540 | 0,605 |
| 1,8 | 0,556 | 0,889 | 0,512 | 0,575 |
| 1,9 | 0,526 | 0,887 | 0,485 | 0,547 |
| 2,0 | 0,500 | 0,886 | 0,463 | 0,523 |
| 2,1 | 0,476 | 0,886 | 0,439 | 0,496 |
| 2,2 | 0,455 | 0,886 | 0,425 | 0,480 |
| 2,3 | 0,435 | 0,886 | 0,409 | 0,461 |
| 2,4 | 0,417 | 0,887 | 0,394 | 0,444 |
| 2,5 | 0,400 | 0,887 | 0,380 | 0,428 |
Примечание. V-коэффициент вариации
Логарифмически нормальное распределение
Для описания закона распределения отказов деталей и элементов металлоконструкций в результате усталостного разрушения широко используют логарифмически нормальное распределение, параметры и показатели которого указаны ниже.
Плотность распределения отказов
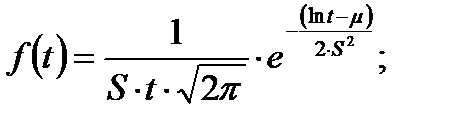
где µ и S параметры, определяемые по результатам испытаний. Так, при испытаниях N изделий до отказа
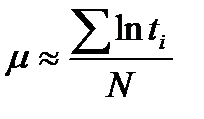
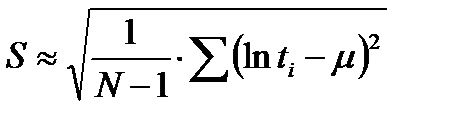
Математическое ожидание наработки до отказа
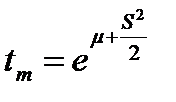
Среднее квадратическое отклонение
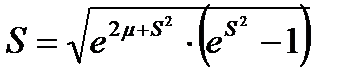
Вероятность безотказной работы можно определять по таблицам для нормального распределения (см. табл. 1) в зависимости от значения квантили
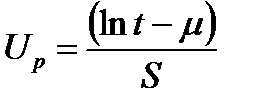
Дата добавления: 2016-12-16; просмотров: 7690;










