Уравнение Бернулли для реальной жидкости

Реальная вязкая жидкость характеризуется наличием сил трения, которые возникают при движении, Силы трения в потоке жидкости. состоящем из множества элементарных струек, играет двоякую роль: - во- первых, благодаря работе сил трения часть механической энергии жидкости переходит в тепло, которое рассеивается: - во- вторых, в связи с наличием сил трения между отдельными элементарными струйками создаются условия, при которых механическая энергия одной струйки передается другой (соседней) струйке, получается «диффузия» механической энергии через боковые поверхности струек; в результате возникает поток энергии движущейся поперек потока жидкости.

Если в место идеальной жидкости рассматривать жидкость реальную, то уравнение Бернулли должно будет существенно измениться. Действительно, если при движении идеальной жидкости ее полная удельная энергия или напор Н сохраняет постоянное значение по длине струйки, то при движении реальной жидкости эта энергия будет убывать по направлению движения. Причиной этого являются неизбежные затраты энергии на преодоление сопротивлений движению, обусловленные внуренним трением и вязкостью жидкости.

Поэтому для струйки реальной жидкости полная удельная

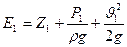
энергия в сечении 1-1 будет всегда больше, чем полная удельная энергия в сечении 2-2.

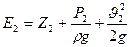
На величину указанных потерь энергии, и уравнение Бернулли в силу этого получает вид

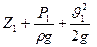
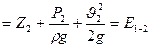
Величина Е_1-2 является мерой энергии потерянной единицей массы жидкости на преодолении сопротивлений при её движении между указанными сечениями.

Соответствущий этой потери удельной энергии напора называют потерей напора между сечениями 1-1 и 2-2 и обозначают h_1-2.

По этому уравнение Бернулли для элементарной струйки реальной жидкости можно представить также и в следующем виде

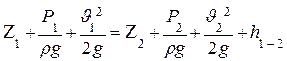
При решении различных практических вопросов о движении жидкости приходится иметь тело с потоками конечных размеров. Уравнение Бернулли для потока реальной жидкости в этом случае может быть получено исходя из рассмотрения потока, как совокупность множества элементарных струек.

Уравнение Бернулли для потока реальной жидкости имеет вид:

,

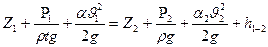где a₁ и a₂ - коэффициент Кориолиса.

Коэффициент Кориолиса учитывает неравномерность распределения скоростей в живом сечении потока . Необходимость использования коэффициента Кориолиса объясняется тем , что в уравнении Бернулли участвуют не фактические местные скорости потока, а средние по сечениям .

Для ламинарного режима движения жидкости коэффициент Кориолиса равен –2, а для турбулентного движения a=1,01…1,03. Для практических расчетов при турбулентном режиме часто коэффициент Кориолиса принимают равным единице.

Уравнение Бернулли для реальной жидкости формулируется так:

Изменение полной удельной энергии, которой обладает поток жидкости в начальном сечении потока, равняется некоторой части от этой энергии, израсходованной на преодоление сопративлений движению жидкости на участке от начального до конечного сечения потока.

График уравнения Бернулли для реальной жидкости имеет следующий вид (рисунок 3).

Рисунок 3.