Расчет двухшарнирных арок. Расчет арок с затяжкой

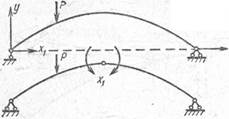Двухшарнирная арка однажды статически неопределима. Основная система может быть образована двумя способами (рис. 7). Балочная основная система проще арочной. Однако арочная система ближе по своей работе к заданной системе. Она в первом приближении уже опре­деляет внутренние силы в двухшарнирной арке. Этим же преимущест­вом будет обладать и первая

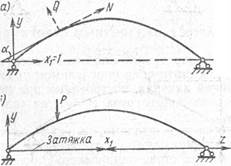Рис. 7 Рис. 8

основная система, если ее рассматривать при совместном действии заданной нагрузки и распора трехшарнирной арки от этой нагрузки. В дальнейшем будем применять первую основ­ную систему.

Для двухшарнирной арки составляется одно каноническое урав­нение метода сил, из которого находится распор или усилие в затяжке:

Х₁ = Н = – Δ_1р/δ₁₁.

Так как ось арки очерчена по кривой у = f (х), то для вычисления перемещений основной системы уже нельзя пользоваться правилом А. Н. Верещагина и необходимо применять интегральную формулу Максвелла — Мора. На практике моменты инерции поперечных сече­ний арок принимаются постоянными или переменными. Наиболее удо­бен для интегрирования такой закон изменения моментов инерции поперечных сечений арки:

I_x = I_с/cos𝜑,

где I_С — момент инерции в среднем сечении арки;

𝜑 — угол наклона касательной к оси арки по отношению к координатной оси х.

Для двухшарнирных арок по конструктивным и эстетическим сооб­ражениям более подходит другой закон:

I_x = I_с×cos𝜑.

При этом высоты поперечных сечений плавно повышаются от опор к середине пролета арки.

При расчете арок приняты следующие пра­вила знаков внутренних усилий: изгибающий момент, вызывающий растяжение во внутренних волокнах, считается положительным; растягивающая нормальная сила принята положительной; попереч­ная сила считается положительной, если она вращает оставшуюся часть по часовой стрелке.

При расчете двухшарнирной арки разложение нагрузки на симметричную и кососимметричную не вносит существенного упрощения. Отметим, что при кососимметричной нагрузке распор Х₁ равен нулю.

Если арка имеет затяжку, то основная система может быть получена разрезанием затяжки (рис. 8).