Понятие об устойчивости
Алгебраические критерии устойчивости
Под устойчивостью понимают способность системы самостоятельно приходить к последующему установившемуся состоянию после приложения воздействия, которое вывело ее из состояния равновесия. Исследование устойчивости является одной из основных задач в теории автоматического управления.
Замкнутая система в силу свойств, обусловленных наличием обратной связи, склонна к неустойчивой работе. В процессе регулирования сигнал с выхода передается на вход группы звеньев системы, среди которых могут быть колебательные элементы. Приложение внешнего воздействия может привести к возмущенному состоянию системы, сопровождающемуся колебаниями регулируемой (выходной) величины. Наличие главной обратной связи будет способствовать поддержанию колебательного процесса и при больших коэффициентах усиления, если параметры системы не обеспечивают необходимого затухания энергии колебаний, может привести к неустойчивой работе, характеризуемой неограниченным возрастанием амплитуды колебаний. В устойчивых системах энергия колебаний с течением времени уменьшается, колебания затухают.
Работа системы в переходном режиме описывается системой дифференциальных уравнений, на основании которых может быть написано одно-единственное дифференциальное уравнение. Его порядок определяется количеством и свойствами динамических звеньев.
Понятие «устойчивость» в смысле его математической трактовки впервые в науку ввел русский ученый А.М.Ляпунов. Он дал строгую и законченную постановку задачи об устойчивости движения и методы ее решения. При исследовании устойчивости системы в общем случае приходится иметь дело с нелинейными задачами. Нелинейное дифференциальное уравнение, характеризующее возмущенное состояние системы, может быть разложено в ряд Тейлора и представлено в виде уравнения первого, второго или n-го приближения, содержащего величины первого, второго или n-го порядка малости. А.М.Ляпунов показал, что все случаи исследования устойчивости следует разделять на две категории: некритических (наиболее часто встречающихся) и критических случаев. Для категории некритических случаев справедливы две следующие теоремы.
Теорема первая. Если вещественные части всех корней характеристического уравнения первого приближения отрицательны, то система будет устойчивой независимо от членов разложения выше первого порядка малости.
Теорема вторая. Если среди корней характеристического уравнения первого приближения найдется по меньшей мере один с положительной вещественной частью, то система будет неустойчивой независимо от членов разложения выше первого порядка малости.
Все критические случаи имеют место лишь тогда, когда среди корней характеристического уравнения первого приближения имеется некоторая группа корней, вещественная часть которых равна нулю, а остальная группа корней имеет отрицательную часть. В этом случае вопрос об устойчивости не может быть решен на основании исследования уравнений первого приближения.
Поскольку уравнение первого приближения можно рассматривать как линеаризованное дифференциальное уравнение, то условия устойчивости А.М.Ляпунова справедливы и для линейных систем. Пусть, например, система описывается линейным дифференциальным уравнением n-го порядка
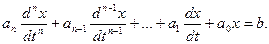 (5.1)
(5.1)
Решение этого уравнения:
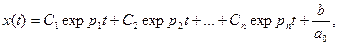 (5.2)
(5.2)
где р1, р2, …рn – корни характеристического уравнения
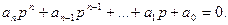 (5.3)
(5.3)
Если система устойчива, то функция x(t) при t, стремящемся к бесконечности, будет приближаться к b/a0, что возможно лишь в том случае, если каждый из членов exp(pit) будет стремиться к нулю. Для этого все корни р1, р2, …рn должны иметь отрицательную вещественную часть. Корни характеристического уравнения можно представить в виде векторов, расположенных в комплексной плоскости (рисунок 5.1). Очевидно, что система будет устойчивой, если все корни располагаются слева от мнимой оси.
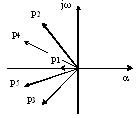
Рисунок 5.1 – Распределение корней в комплексной плоскости
В случае, если один вещественный корень или пара комплексно-сопряженных корней располагаются на мнимой оси, система оказывается на границе устойчивости. Системы, у которых имеется одна пара мнимых корней, могут совершать незатухающие колебания (автоколебания). Эти системы часто относят к неустойчивым, так как они практически неработоспособны. Линейные системы, характеристические уравнения которых имеют один нулевой корень при всех остальных корнях, расположенных левее мнимой оси, называют нейтрально-устойчивыми. Для того чтобы все корни оказались в левой полуплоскости, можно воздействовать на коэффициенты характеристического уравнения, которые, согласно теореме Виета, связаны с корнями непрерывными зависимостями.
При исследовании устойчивости системы возможно решение следующих задач:
- выяснение, является ли устойчивой система при заданных параметрах;
- определение допустимых изменений некоторых параметров (при неизменных остальных параметрах и заданной структуре) без нарушения устойчивости системы;
- анализ структуры системы и определение параметров, при которых она может стать устойчивой (анализ структурной устойчивости).
Первая задача может быть решена различными методами. Можно определить корни характеристического уравнения и по ним установить знаки их вещественных частей. Однако такой метод может быть использован, когда порядок характеристического уравнения ниже третьего. Уже для кубического уравнения трудно определить корни, не говоря об уравнениях более высоких порядков. Кроме того, для определения устойчивости совершенно не обязательно знать значение корней характеристического уравнения. Достаточно убедиться только в отрицательности вещественных частей корней. Поэтому представляется целесообразным воспользоваться другими, более простыми методами определения устойчивости, основанными на установлении факта отрицательности вещественных частей корней без нахождения их значения. Такие методы основываются на использовании критериев устойчивости, например алгебраических критериев Рауса и Гурвица, частотных критериев Михайлова и Найквиста, а также условий устойчивости, определяемых логарифмическими частотными характеристиками.
Для решения второй задачи могут быть использованы методы выделения областей устойчивости.
5.2 Алгебраические критерии устойчивости
5.2.1 Критерий Рауса
Алгебраические критерии устойчивости позволяют установить, устойчива система или нет, по результатам алгебраических действий над коэффициентами характеристического уравнения. Условия, устанавливающие факт отрицательности вещественных частей корней, и будут являться критериями устойчивости. Впервые подобный критерий был предложен английским математиком Э.Раусом в 1877 году в виде алгоритма.
Пусть дано характеристическое уравнение
а0 рn + a1 pn-1 + ... + an-1 p + an =0. (5.4)
В первой строке таблицы Рауса записывают в порядке возрастания индексы коэффициентов характеристического уравнения (6.4), имеющие четный порядок: а0 а2 а4 а6 …
Во второй строке коэффициенты с нечетным порядком: а1 а3 а5 а7 .. . Остальные строки состоят из элементов, определяемых по формуле
Ck,i = Ck+1,i-2 – ri Ck+1,i-1 (5.5)
ri = C1,i-2 / C1,i-1 (5.6)
где k – номер столбца;
i – номер строки.
Число строк таблицы Рауса равно (n +1). Коэффициенты критерия Рауса сведены в таблицу 5.1.
Таблица 5.1 - Коэффициенты критерия Рауса
| Коэффициент ri | ССтро- кка i | Столбец k | ||
| C11 = a0 | C21 = a2 | C31 = a4 | ||
| C12 = a1 | C22 = a3 | C32 = a5 | ||
| r3 = C11/C12 = a0/a1 | C13 = C21 – r3C22 | C23 = C31 – r3C32 | C33 = C41 – r3C42 | |
| ........ | .... | ....... | ........ | ........ |
| Rn+1 = C1n /C1n+1 | ni +1 | C1n+1 = C2n-1 – rn+1 C2n | C2n+1 = C3n-1 – rn+1 C3n | C1n+1 = C4n-1 – rn+1 C4n |
Критерий Рауса: для того, чтобы система была устойчива, необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса имели один и тот же знак, т.е. при а0>0 были положительными:
С11 = а0 >0; C12 = a1 >0; C13 >0; ..... C1,n+1 >0 (5.7)
5.2.2 Критерий Гурвица
В 1895 году немецкий математик Гурвиц А. предложил следующий метод: из коэффициентов характеристического уравнения (5.4) сначала строят главный определитель
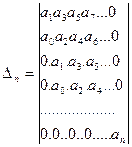 (5.8)
(5.8)
Главный определитель составляется так, что по главной диагонали выписываются коэффициенты уравнения начиная с а1 в возрастающем порядке до аn . От каждого коэффициента главной диагонали по вертикали вверх выписываются коэффициенты с возрастающими и вниз - с убывающими индексами. Места в матрице коэффициентов с индексами больше n и меньше 0 заполняются нулями. Вещественные части корней будут отрицательными в том случае, если все коэффициенты уравнения и диагональные миноры главного определителя будут положительными.
Отчеркивая в главном определителе Гурвица диагональные миноры, получаем определители Гурвица низшего порядка:
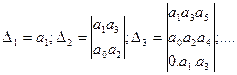
Критерий Гурвица: для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы все определители Гурвица имели знаки, одинаковые со знаком первого коэффициента а0 характеристического уравнения, т.е. при а 0 >0 были положительными
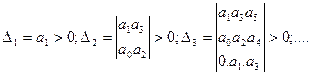 (5.9)
(5.9)
Обычно критерий Гурвица применяется для систем с n ≤ 4, выше используется критерий Льенара – Шипара. В последнем столбце главного определителя (6.8) отличен от нуля только аn , поэтому
Δn = an Δn-1 . (5.10)
Поэтому для проверки устойчивости САУ достаточно найти Δ1 – Δn-1. Если все определители Δ1 – Δn-1 >0, а главный Δn = 0, то САУ находится на границе устойчивости. Это возможно только в двух случаях: an = 0 или Δn-1 >0. В первом (an = 0) САУ находится на границе апериодической устойчивости (один из корней si = 0); во втором (Δn-1 >0) на границе колебательной устойчивости (2 комплексно-сопряженных корня находятся на мнимой оси si = jωi; si+1 = -jωi).
Для систем, имеющих характеристические уравнения n ≥ 5 удобно применять одну из модификаций критерия Гурвица, предложенную в в 1914 году Льенаром П. и Шипаром Р.: для того чтобы САУ была устойчива, необходимо и достаточно, чтобы выполнялись неравенства
a0 >0, a1 >0, ..........an >0 (5.11)
Δ1 >0, Δ3 >0, Δ5 >0......... – нечетные определители
или
a0 >0, a1 >0, ..........an >0 (5.12)
Δ2 >0, Δ4 >0, Δ6 >0......... – четные определители
Очевидно, что этот критерий требует в два раза меньше раскрытий определителей, чем критерий Гурвица, поэтому особенно удобен при исследовании устойчивости САУ высшего порядка.
Рассмотрим выражение критерия Гурвица для некоторых уравнений.
Уравнение третьего порядка
a0 р3 +а1 р2 +а2 р + а3 = 0.
Главный определитель
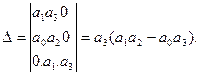
Условие Гурвица (а1 а2 –а0 а3 ) > 0, а3 (а1 а2 – а0 а3 ) > 0, ai > 0, i = 1, 2, 3.
Следовательно, система будет устойчивой, если все коэффициенты а0,а1,a2,а3 положительны и а1a2 – a0a3 >0, т.е. а1a2 > a0a3. Для уравнений третьего порядка при положительных коэффициентах а0,а1,a2,а3 и выполнения условия а1a2 > a0a3 называется критерием устойчивости Вышнеградского.
Уравнение четвертого порядка
а0 р4 +al p3 +a2 p2 + а3 р + а4 = 0.
Главный определитель
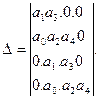
Условия Гурвица
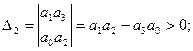
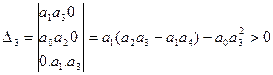
или
Δ3 = а3(а1а2 - а0а3) – а12 а4 = а3 Δ2 – а12 а4 >0.
Определитель Δ3 может быть положительным лишь при условии Δ2 > 0. Поэтому условие устойчивости для уравнения четвертого порядка может быть выражено соотношением
а3 (а1а2 –a3 a0) – а12 а4 > 0.
Уравнение пятого порядка
а0р5 + а1р4 +а2р3 +а3р2 +а4р + а5 = 0.
Система, описываемая уравнением пятого порядка, устойчива, если
Δ3 = а1(а2а3 – а1а4) – а0а32 >0.
Δ4 = (a3a4 -а2а5)(а1а2 -а0а3)- (а1а4 -а0а5)2 > 0.
Примеры:
D(s) = 12S4 + 2S2 +4S + 50 = 0 - система неустойчива, т.к. а1 = 0.
D(s) = 3S5 +10S4 + 5S3 - 7S2 +S + 10 = 0 - система неустойчива, т.к. а3 = -7<0.
D(s) = 2S3 + 6S2 +10S + 15 = 0 - система устойчива, т.к. а1a2 > a0a3 или 6 ∙ 10>2 ∙ 15
| <== предыдущая лекция | | | следующая лекция ==> |
| Логарифмические частотные характеристики систем | | | Что такое гидравлика |
Дата добавления: 2016-11-04; просмотров: 1426;










