Глава 6. Сигналы с ограниченным спектром

Для восстановления сигнала по его спектру необходимо учитывать все составляющие с частотами, лежащими в интервале от нуля до бесконечности. Однако с физической точки зрения такая процедура принципиально неосуществима. К тому же вклад спектральных составляющих при 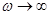пренебрежимо мал в силу ограниченности энергии сигналов. Наконец, любое реальное устройство, предназначенное для передачи и обработки сигналов, имеет конечную ширину полосы пропускания. Поэтому вполне реалистичной представляется математическая модель сигнала, имеющая такое свойство: спектральная плотность колебания отлична от нуля лишь в пределах некоторой полосы частот конечной протяженности. Подобный сигнал называют сигналом с ограниченным спектром.

Пусть 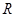– конечный отрезок оси частот. Спектральная плотность 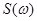сигнала 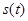с ограниченным спектром удовлетворяет условиям 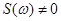при , при 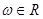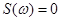всех других значениях частоты.

Математическую модель сигнала с ограниченным спектром во временной области можно получить из формулы обратного преобразования Фурье:

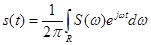. (35)

Рассмотрим колебание с постоянной вещественной спектральной плотностью 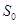в пределах отрезка оси частот от нуля до верхней граничной частоты 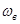; вне этого отрезка спектральная плотность сигнала обращается в нуль:

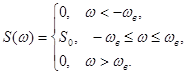(36)

Мгновенные значения такого сигнала

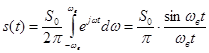(37)

График (рис. 13), построенный по формуле (37), имеет вид осциллирующей кривой, четной относительно начала отсчета времени. С увеличением верхней граничной частоты спектра возрастают как центральный максимум, так и частота осцилляции.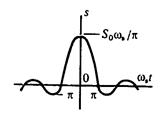
Рис. 13

Свойство ограниченности спектра позволяет находить интересные и важные классы ортогональных сигналов.

Рассмотрим два идеальных сигнала 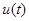и 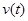. Оба эти сигнала имеют одинаковые параметры 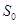и 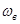(36), однако сигнал 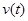запаздывает по отношению к сигналу 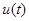на время 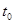, так что его спектральная плотность .

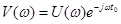Скалярное произведение этих сигналов, вычисленное через спектральные плотности,

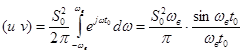. (38)

Скалярное произведение обращается в нуль и два одинаковых по форме сигнала оказываются ортогональными, если временной сдвиг между ними удовлетворяет условию .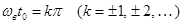

Минимально возможный сдвиг, приводящий к ортогонализации, получается при :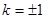

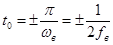. (39)

Таким образом, определен способ построения бесконечного ортогонального базиса, который может служить координатной системой для разложения произвольного сигнала со спектром, ограниченным частотой .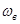

Одним из фундаментальных положений теории сигналов является теорема Котельникова. Эта теорема устанавливает возможность сколь угодно точного восстановления мгновенных значений сигнала с ограниченным спектром исходя из отсчетных значений (выборок), взятых через равные промежутки времени.

Как было показано, любые два сигнала с ограниченным спектром, принадлежащие семейству

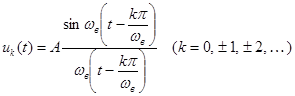, (40)

являются ортогональными. Путем соответствующего выбора амплитудного множителя 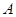можно добиться того, чтобы норма каждого из этих сигналов стала единичной. В результате будет построен ортонормированный базис, позволяющий разложить произвольный сигнал с ограниченным спектром в обобщенный ряд Фурье.

Достаточно рассмотреть лишь функцию

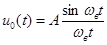, (41)

так как норма любого сигнала 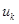одинакова независимо от сдвига во времени. Поскольку

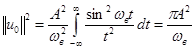, (42)

функции 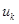будут ортонормированными, если

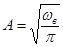. (43)

Бесконечная совокупность функций

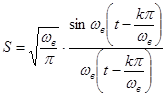(44)

образует базис Котельникова в линейном пространстве низкочастотных сигналов со спектрами, ограниченными сверху значением 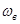. Отдельная функция 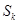называется 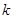-й отсчетной функцией.

Если 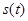– произвольный сигнал, спектральная плотность которого отлична от нуля лишь в полосе частот 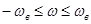, то его можно разложить в обобщенный ряд Фурье по базису Котельникова:

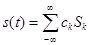. (45)

Коэффициентами ряда служат, как известно, скалярные произведения разлагаемого сигнала и 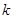-й отсчетной функции

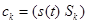. (46)

Можно убедиться, что 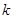-я отсчетная функция в пределах отрезка 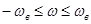имеет спектральную плотность, равную 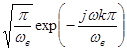. Тогда, если 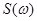– спектр сигнала 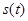, то

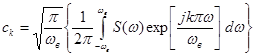(47)

Величина в фигурных скобках есть не что иное, как 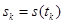, т. е. мгновенное значение сигнала 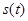в 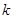-й отсчетной точке .

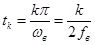Таким образом,

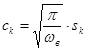, (48)

откуда следует выражение ряда Котельникова:

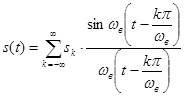. (49)

Теорему Котельникова на основании последнего равенства принято формулировать так: произвольный сигнал, спектр которого не содержит частот выше 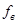, Гц, может быть полностью восстановлен, если известны отсчетные значения этого сигнала, взятые через равные промежутки времени 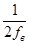с.

Значительные преимущества при передаче, обработке и хранении информации обеспечиваются в случае переход от непрерывного сигнала к дискретному. В связи с тем, что каждому из дискретных значений конечного множества можно сопоставить число, возникает возможность перейти к цифровому представлению информации, что позволит использовать ЭВМ при ее обработке.

Для выполнения этого перехода над непрерывной функцией непрерывного аргумента осуществляются преобразования, называемые квантованием по времени или дискретизацией и квантованием по уровню. В дальнейшем во избежание путаницы под дискретизацией будем понимать квантование по времени, а квантование по уровню будем называть просто квантованием.

Дискретизация сводится к замене непрерывной по аргументу функции, функцией дискретного аргумента. В результате непрерывная функция отображается конечным числом ее мгновенных значений, взятых через определенные (равные или неравные) промежутки времени .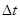

В связи с этим возникает вопрос о возможности сколь угодно точного восстановления мгновенных значений процесса, исходя из отсчетных или выборочных значений, взятых через определенные интервалы. Дискретизация должна производиться так, чтобы по отсчетным значениям или коэффициентам разложения можно было получить воспроизводящую функцию, которая с заданной точностью отображает исходную функцию.

Восстановление непрерывной функции по конечному числу ее значений на конечном интервале времени приводит к погрешности, зависящей от числа взятых значений этой функции на этом интервале, т. е. от частоты дискретизации.

Таким образом, при дискретизации приходится решать вопрос о том, как часто следует производить отсчеты функции, т. е. каков должен быть шаг дискретизации .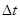

Ответ на этот вопрос дает теорема Котельникова, в соответствии с которой величина шага дискретизации 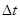не должна превышать 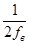, где 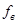– верхняя частота спектра дискретизируемого сигнала.

Оценим ошибку, возникающую при аппроксимации произвольного сигнала рядом Котельникова. Если 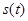– произвольный сигнал, то его можно представить суммой 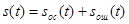, в которую входит сигнал 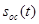со спектром, ограниченным значением 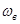, а также сигнал ошибки аппроксимации 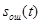со спектром, занимающим в общем случае бесконечную полосу частот .

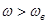Спектры указанных сигналов не перекрываются, поэтому сигналы 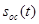и 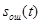ортогональны, а их энергии, т. е. квадраты норм, складываются:

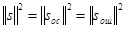
В качестве меры ошибки аппроксимации можно принять норму сигнала ошибки.

После дискретизации непрерывного сигнала он может быть представлен совокупностью отсчетов, каждый из которых, вообще говоря, может иметь бесконечное множество значений. Реальные устройства, работающие с этими сигналами, имеют конечную разрешающую способность, т. е. весьма малый, но не нулевой интервал, внутри которого все разные значения отсчетов воспринимаются как одинаковые. Сказанное свидетельствует о целесообразности квантования. Квантование функции есть, по сути, отображение непрерывного множества ее возможных значений на конечное подмножество ее значений, каждое из которых представляется в виде одного из заранее определенных дискретных уровней, называемых уровнями квантования.

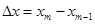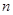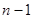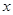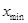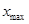Под шагом квантования понимается разность значений соседних уровней квантования. Число уровней квантования на единицу больше числа интервалов квантования. Если квантуемая функция ограничена диапазоном от до , то .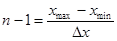

При квантовании обычно истинное значение функции 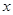отождествляется или заменяется значением 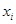, соответствующим ближайшему уровню квантования.

Естественно, замена истинных значений на значения уровней квантования приводит к ошибке 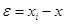, называемой ошибкой или шумом квантования.

Обычно полагается, что при равномерном квантовании, когда 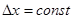, шум квантования – случайная величина с равномерным законом распределения в пределах шага квантования. Максимальная ошибка квантования не превосходит половины шага квантования .

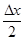Таким образом, ошибка квантования уменьшается с уменьшением шага квантования 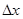. Однако при уменьшении шага растет число уровней квантования, а, следовательно, растет и разрядность чисел, требуемая для их представления. Кроме того, при уменьшении шага квантования его величина может оказаться сопоставимой с уровнем помех. Так что к выбору величины шага квантования необходимо подходить с тех же позиций, что и к выбору шага дискретизации, т. е. выбирать оптимальный шаг квантования с точки зрения обеспечения минимума уровней квантования и заданной величины ошибки квантования.

Таким образом, после выполнения операций дискретизации и квантования непрерывный сигнал представляется конечной последовательностью отсчетов, величина которых может принимать только вполне определенные значения, соответствующие уровням квантования. Если сопоставить каждому уровню квантования число, то непрерывный сигнал в результате выполнения операций дискретизации и квантования будет представлять собой последовательность чисел из конечного интервала, т. е. будет представлено в цифровой форме.