Глава 3. Векторное представление сигналов

Сигнал можно рассматривать как вектор в специальном образом сконструированном бесконечномерном пространстве.

Пусть 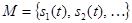– множество сигналов. Причиной объединения этих объектов является наличие некоторых свойств, общих для всех элементов множества .

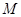Исследование свойств сигналов, образующих такие множества, становится особенно плодотворным тогда, когда удается выражать одни элементы множества через другие элементы. Принято говорить, что множество сигналов наделено при этом определенной структурой. Так, применительно к электрическим колебаниям известно, что они могут складываться, а также умножаться на произвольный масштабный коэффициент. Это дает возможность в множествах сигналов ввести структуру линейного пространства.

Множество сигналов 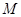образует вещественное линейное пространство, если справедливы следующие аксиомы:

1. Любой сигнал 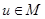при любых 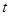принимает лишь вещественные значения.

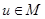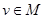2. Для любых и существует их сумма 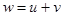, причем 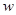также содержится в 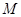. Операция суммирования коммутативна: 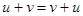и ассоциативна: .

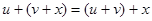3. Для любого сигнала 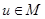и любого вещественного числа 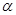определен сигнал 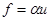, который .

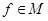4. Множество 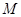содержит особый нулевой элемент 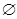, такой, что 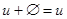для всех .

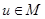Если математические модели сигналов принимают комплексные значения, то, допуская в аксиоме 3 умножение на комплексное число, приходим к понятию комплексного линейного пространства.

Элементы линейных пространств часто называют векторами, подчеркивая аналогию свойств этих объектов и обычных трехмерных векторов.

Как и в обычном трехмерном пространстве, в линейном пространстве сигналов можно выделить специальное подмножество, играющее роль координатных осей.

Говорят, что совокупность векторов 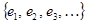, принадлежащих 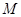, является линейно независимой, если равенство 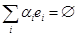возможно лишь в случае одновременного обращения в нуль всех числовых коэффициентов .

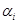Система линейно независимых векторов образует координатный базис в линейном пространстве. Если дано разложение некоторого сигнала 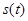в виде

,

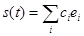то числа 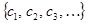являются проекциями сигнала 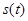относительно выбранного базиса.

Для того чтобы продолжить и углубить геометрическую трактовку теории сигналов, необходимо ввести новое понятие, которое по своему смыслу соответствует длине вектора. Это позволит не только придать точный смысл высказыванию вида «первый сигнал больше второго», но и указать, на сколько он больше. Длину вектора в математике называют его нормой. Линейное пространство сигналов 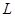является нормированным, если каждому вектору 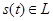однозначно сопоставлено число 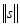– норма этого вектора. Должны выполняться следующие аксиомы нормированного пространства:

1. Норма неотрицательна, т. е. 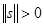. Норма 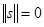тогда и только тогда, когда .

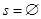2. Для любого числа 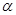справедливо равенство .

3. Есл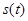и и 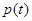– два вектора из 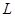, то выполняется неравенство треугольника: .

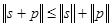Можно предложить разные способы введения нормы сигналов. Чаще всего полагают, что вещественные аналоговые сигналы имеют норму

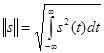, (9)

причем из двух возможных значений корня выбирается положительное.

Квадрат нормы носит название энергии сигнала

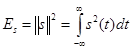. (10)

Именно такая энергия выделяется в резисторе с сопротивлением 1 Ом, если на его зажимах существует напряжение .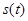

Теперь необходимо ввести еще одно фундаментальное понятие, которое обобщало бы обычное представление о расстоянии между точками в пространстве.

Говорят, что линейное пространство 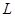становится метрическим пространством, если каждой паре элементов 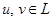сопоставлено неотрицательное число 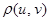, называемое метрикой, или расстоянием между этими элементами. Метрика, независимо от способа ее определения, должна подчиняться аксиомам метрического пространства:

1. 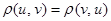(рефлексивность метрики).

2. 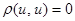при любых .

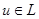3. Каков бы ни был элемент 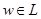, всегда .

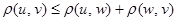Обычно метрику определяют как норму разности двух сигналов:

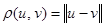. (11)

Норму, в свою очередь, можно понимать как расстояние между выбранным элементом пространства и нулевым элементом: .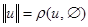

Введя в множестве сигналов структуру линейного пространства, определив норму и метрику, мы, тем не менее, лишены возможности вычислить такую характеристику, как угол между двумя векторами. Это удается сделать, сформулировав важное понятие скалярного произведения элементов линейного пространства.

Напомним, что если в обычном трехмерном пространстве известны два вектора 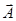и 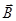, то квадрат модуля их суммы

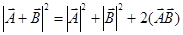, (12)

где 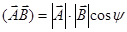– скалярное произведение этих векторов, зависящее от угла 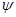между ними.

Действуя по аналогии, вычислим энергию суммы двух сигналов 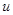и :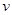

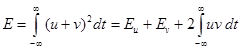. (13)

В отличие от самих сигналов их энергии неаддитивны – энергия суммарного сигнала содержит в себе так называемую взаимную энергию

.

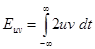Сравнивая между собой формулы (12) и (13), определим скалярное произведение вещественных сигналов 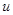и :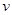

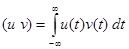, (14)

а также косинус угла между ними

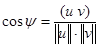. (15)

Скалярное произведение обладает следующими свойствами:

1. ;

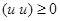2. ;

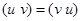3. 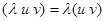, где 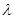– вещественное число;

4. .

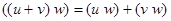Линейное пространство с таким скалярным произведением, полное в том смысле, что оно содержит в себе все предельные точки любых сходящихся последовательностей векторов из этого пространства, называется вещественным гильбертовым пространством .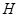

Справедливо фундаментальное неравенство Коши – Буняковского

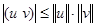. (16)

Из данного неравенства вытекает, в частности, что косинус угла между векторами в пространстве сигналов не превышает единицы.

Два сигнала 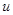и 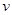называются ортогональными, если их скалярное произведение, а значит, и взаимная энергия равны нулю:

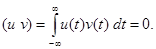(17)

Пусть 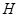– гильбертово пространство сигналов с конечным значением энергии. Эти сигналы определены на отрезке времени 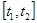, конечном или бесконечном. Предположим, что на этом же отрезке задана бесконечная система функций 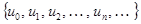, ортогональных друг другу и обладающих единичными нормами:

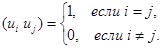(18)

Говорят, что при этом в пространстве сигналов задан ортонормированный базис.

Разложим произвольный сигнал 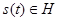в ряд:

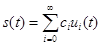. (19)

Представление (19) называется обобщенным рядом Фурье сигнала 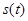в выбранном базисе.

Коэффициенты данного ряда находят следующим образом. Возьмем базисную функцию 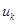с произвольным номером 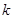, умножим на нее обе части равенства (19) и затем проинтегрируем результаты по времени:

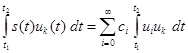. (20)

Ввиду ортонормированности базиса в правой части равенства (20) останется только член суммы с номером 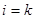, поэтому

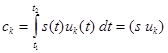. (21)

Возможность представления сигналов посредством обобщенных рядов Фурье является фактом большого принципиального значения. Вместо того чтобы изучать функциональную зависимость в несчетном множестве точек, мы получаем возможность характеризовать эти сигналы счетной (но, вообще говоря, бесконечной) системой коэффициентов обобщенного ряда Фурье .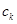

Одним из примеров ортонормированного базиса является система тригонометрических функций с кратными частотами дополненная постоянной составляющей:

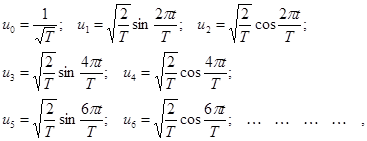(22),

где 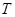– период сигнала.

Выполнив ортогональное разложение сигнала 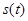в этом базисе, т. е. вычислив коэффициенты

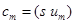, (23)

получим спектральное разложение

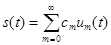, (24)

справедливое на всей бесконечности оси времени.

Ряд вида (24) называется рядом Фурье данного сигнала.

Контрольные вопросы к лекции 8

8-1. Что называется сигналом?

8-2. Какой сигнал называется аналоговым?

8-3. Какой сигнал называется дискретным?

8-4. Какой сигнал называется импульсным?

8-5. Какой сигнал называется цифровым?

8-6. Какой сигнал называется детерминированным?

8-7. Какие параметры последовательности прямоугольных импульсов являются основными?

8-8. Как связаны циклическая и круговая частота последовательности прямоугольных импульсов?

8-9. Что называется скважностью последовательности прямоугольных импульсов?

8-10. Что называется коэффициентом заполнения последовательности прямоугольных импульсов?

8-11. Как определяется среднее значение последовательности прямоугольных импульсов?

8-12. Что называется абсолютным спадом крыши импульса?

8-13. Что представляет собой функция Хевисайда?

8-14. Что представляет собой функция Дирака?

8-15. Какое множество сигналов образует вещественное линейное пространство?

8-16. Какое множество сигналов образует комплексное линейное пространство?

8-17. Какая система векторов является линейно независимой?

8-18. Какое линейное пространство векторов является нормированным?

8-19. Какими свойствами должна обладать норма вектора?

8-20. Какое название носит квадрат нормы?

8-21. Какое линейное пространство называется метрическим?

8-22. Какими свойствами должна обладать метрика?

8-23. Как определяется скалярное произведение двух векторов в трехмерном пространстве?

8-24. Какими свойствами обладает скалярное произведение двух векторов в трехмерном пространстве?

8-25. Какие сигналы называются ортогональными?

8-26. Что называется ортонормированным базисом линейного пространства?

8-27. Как выглядит разложение произвольного сигнала в обобщенный ряд Фурье в произвольном ортонормированном базисе?

8-28. Приведите пример ортонормированного базиса.