Метод вспомогательных секущих сфер.
При выборе метода руководствуются тем, что вспомогательные секущие поверхности – посредники должны давать в своем пересечении с каждой заданной поверхностью наиболее простые линии,а именно – прямые или окружности. В приведенной задаче показано, что при пересечении конической поверхности плоскостью проще всего строятся окружности, которые могут получаться если конус пересекает плоскость , расположенная параллельно основанию конуса и перпендикулярная оси его вращения.Это справедливо для прямого кругового конуса, имеющего в основании круг. Из рисунка видно, что сами сечения встречаются в точках 1 и 2, точке 4 и т.д. Эти точки называются точки встречи поверхностей . Плоскость Δ пересекает оба конуса по образующим, которые встречаются в точке 3. Если для построения линии пересечения точек недостаточно, то вводятся дополнительно вспомогательные плоскости – посредники и получают достаточное количество точек, принадлежащих заданным поверхностям. В каждой задаче количество секущих плоскостей разное и зависит от особенностей пересекающихся поверхностей. Методом секущих плоскостей можно решить любую позиционную задачу, но иногда ее решение бывает достаточно сложным и требуется использовать способы решения , позволяющие решать задачи более простым и точным способом.
Пересечение поверхностей общего положения
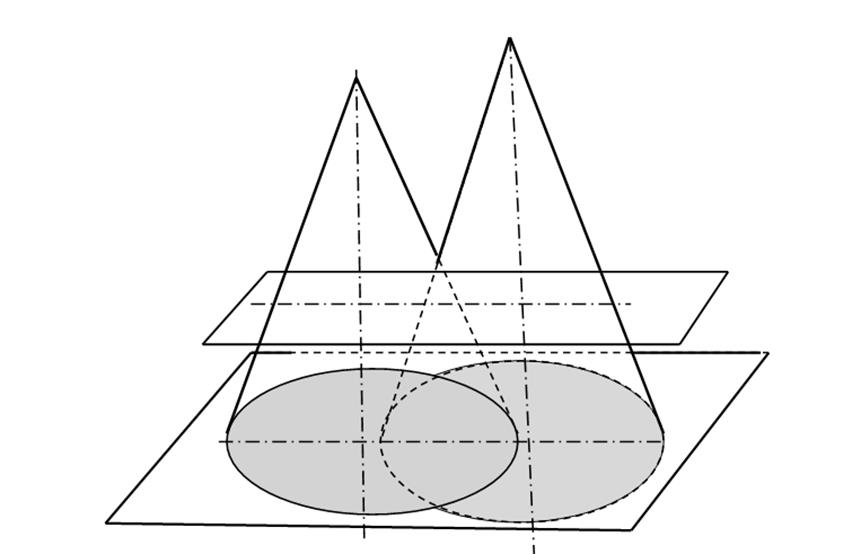
Задача: Построение линии пересечения двух конусов
Алгоритм решения:
Построение линии пересечения двух конусов
Дата добавления: 2016-07-27; просмотров: 2630;










