Common /cblock/ a,ak,m
!входные данные; при указанных значениях
!результат для контроля: h = 0.8956242
!длина волны; размерности alambda и t одинаковые
alambda = 0.85
!толщина волноведущего слоя
t = 5.
!отн. диэл. проницаемость покрытия
e1 = 2.11
!отн. диэл. проницаемость волноведущего слоя
e2 = 2.14
!отн. диэл. проницаемость подложки
e3 = 2.12
!номер моды
m = 1
!погрешность значения корня
eps = 1e-6
!вычисляется коэффициент A
a = 2 * sqrt(e2-e3) * t/alambda
!вычисляется коэффициент K
ak = (e2-e1) / (e2-e3)
!обращение к функции решения уравнения F(x)=0
aksi = dih(1e-10,1.,eps)
!определение h
h = aksi * 2*3.14159/alambda * sqrt(e2-e3)
!вывод результата
print *, h
End
!--------------------------------------------------------------
!Функция решения уравнения F(x)=0 методом дихотомии
!с точностью eps при условии, что корень лежит в
!интервале от a до b
Function dih(a,b,eps)
!цикл, пока не достигнута требуемая точность
Do while((b-a) .gt. eps)
!c = середина отрезка [a,b]
c=(a+b)/2
!проверка знака функции в середине отрезка [a,b]
If(f(c) .gt. 0) then
!обновление правой границы если F(c) > 0
b=c
Else
!обновление левой границы если F(c) = 0
a=c
Endif
Enddo
!dih -- решение; F(dih) = 0 с точностью до eps
dih=(a+b)/2
Return
End
!--------------------------------------------------------------
!Функция F(x) для функции dih
Function f(x)
!переменные, получаемые из beta1
Common /cblock/ a,ak,m
f1 = atan( sqrt(1/x**2-1) )
f1 = (f1 + atan(sqrt(ak/x**2-1))) / 3.14159
f = a*x - m - f1
Return
End
!--------------------------------------------------------------
3.3. Метод аппроксимации
При решении уравнения (3.3) методом “половинного деления” основная трудность обусловлена необходимостью многократных вычислений достаточно “неудобной” функции 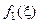 . Метод аппроксимации позволяет преодолеть эти трудности.
. Метод аппроксимации позволяет преодолеть эти трудности.
Основная идея метода заключается в сведении уравнения (3.3) к квадратному путем введения аппроксимирующей функции для правой части уравнения (3.3). В результате такой аппроксимации решение (3.3) записывается в явном виде, а необходимая точность достигается простой итерационной процедурой, что значительно увеличивает быстродействие и эффективность алгоритма.
3.3.1 Алгоритм решения. На рисунке 3.2 представлена для примера зависимость 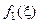 в правой части (3.3) от параметра
в правой части (3.3) от параметра 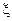 для Н-мод при разных значениях
для Н-мод при разных значениях 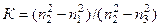 . Аналогичную форму имеют кривые и для Е-мод (рис.3.2).
. Аналогичную форму имеют кривые и для Е-мод (рис.3.2).
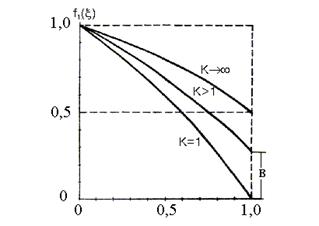
Рис. 3.2. К решению трансцендентного уравнения методом аппроксимации.
Поскольку в (3.4) берутся главные значения арктангенсов, величина 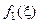 лежит в пределах
лежит в пределах
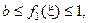 (3.9)
(3.9)
где b – параметр, определяемый из (3.4) при 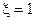 :
:
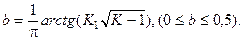 (3.10)
(3.10)
С учетом явного вида 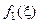 (рис.3.2) аппроксимирующая ее функция вводится следующим образом:
(рис.3.2) аппроксимирующая ее функция вводится следующим образом:
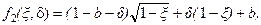 (3.11)
(3.11)
где 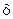 – параметр, характеризующий “кривизну”.
– параметр, характеризующий “кривизну”.
При условии 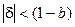 функции
функции 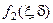 и
и 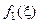 имеют следующие свойства:
имеют следующие свойства:
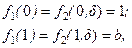 (3.12)
(3.12)
а их производные по параметру 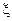 :
:
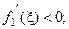
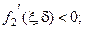
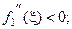
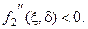 (3.13)
(3.13)
Выполнение условий (3.12), (3.13) означает, что обе функции имеют одинаковые граничные значения, монотонно убывают и являются выпуклыми в интервале 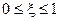 .
.
Из условий (3.12), (3.13) следует, что функция 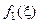 и аппроксимирующая функция
и аппроксимирующая функция 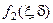 (3.11) не пересекаются. Однако, подбором параметра
(3.11) не пересекаются. Однако, подбором параметра 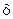 можно в любой точке
можно в любой точке 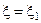 добиться выполнения условия
добиться выполнения условия 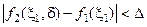 , где
, где 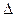 – сколь угодно малая величина. Параметр
– сколь угодно малая величина. Параметр 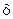 выбирается исходя из условия предельного равенства
выбирается исходя из условия предельного равенства 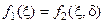 . С учетом формулы (3.11) устанавливается связь между абсциссами точек пересечения и значениями параметра
. С учетом формулы (3.11) устанавливается связь между абсциссами точек пересечения и значениями параметра 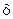 :
:
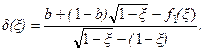 (3.14)
(3.14)
Предельные значения 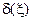 соответствуют граничным значениям интервала
соответствуют граничным значениям интервала 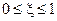 :
:
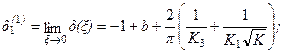 (3.15а)
(3.15а)
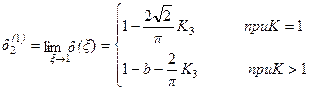 (3.15б)
(3.15б)
Задание: получить соотношение (3.15,а) – (3.15,б).
Из выражения (3.14) следует, что функция 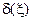 убывает монотонно в пределах
убывает монотонно в пределах 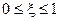
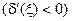 , т.е. между
, т.е. между 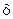 и
и 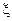 существует взаимно-однозначное соответствие при следующих ограничениях на параметры планарного диэлектрического волновода (см. (3.1), (3.4) и таблицу 1):
существует взаимно-однозначное соответствие при следующих ограничениях на параметры планарного диэлектрического волновода (см. (3.1), (3.4) и таблицу 1):
Таблица 1
| Мода | Симметричный волновод (n1=n3) | Несимметричный волновод (n3>n1) |
| Н Е | без ограничений
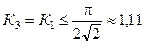
| К 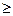 2,33 2,33
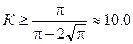
|
На рисунке 3.3. для примера представлены зависимость 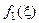 и графики функций, аппроксимирующих ее с “недостатком”
и графики функций, аппроксимирующих ее с “недостатком” 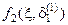 и с “избытком”
и с “избытком” 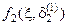 .
.
Заменяя функцию 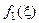 в (3.3) на аппроксимирующую ее функцию
в (3.3) на аппроксимирующую ее функцию
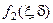 , трансцендентное уравнение (3.3) сводится к квадратному относительно переменной
, трансцендентное уравнение (3.3) сводится к квадратному относительно переменной 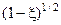 :
:
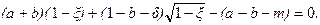 (3.16)
(3.16)
Физическим решением этого уравнения относительно 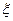 является
является 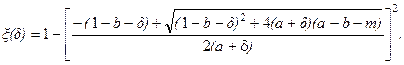 (3.17)
(3.17)
Подставляя 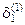 и
и 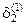 в (3.17), находим два значения
в (3.17), находим два значения 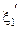 и
и 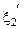 абсцисс точек пересечения функции
абсцисс точек пересечения функции 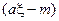 в левой части (3.3) с аппроксимирующими функциями
в левой части (3.3) с аппроксимирующими функциями 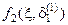 и
и 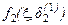 правой части уравнения (3.3) (рис. 3.3).
правой части уравнения (3.3) (рис. 3.3).
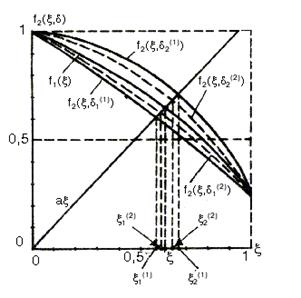
Рис. 3.3. Аппроксимирующие функции.
Из рисунка 3.3 следует, что решением уравнения (3.3) является значение 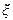 , лежащее в интервале
, лежащее в интервале
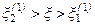 . (3.18)
. (3.18)
Решение на первом шаге итерации записывается в виде
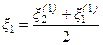 . (3.19)
. (3.19)
Если точность 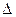 полученного решения, определяемая величиной интервала
полученного решения, определяемая величиной интервала 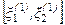 недостаточна, то нужно использовать метод последовательных подстановок. Для этого вычисленные значения
недостаточна, то нужно использовать метод последовательных подстановок. Для этого вычисленные значения 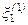 и
и 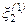 подставляют в (3.14) и находят новые значения
подставляют в (3.14) и находят новые значения 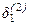 и
и 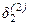 . Затем эти значения подставляют в (3.17) и определяют два новых решения
. Затем эти значения подставляют в (3.17) и определяют два новых решения 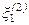 и
и 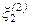 , причем
, причем
 . (3.20)
. (3.20)
Аналогично (3.19) записывается новое решение 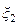 на втором шаге итерации.
на втором шаге итерации.
Если заданная точность 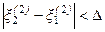 не достигнута, то итерационный процесс продолжается дальше. Общие формулы для j-й итерации имеют следующий вид:
не достигнута, то итерационный процесс продолжается дальше. Общие формулы для j-й итерации имеют следующий вид:
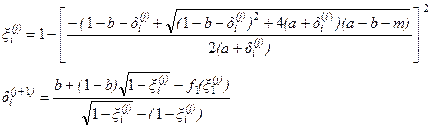 , (3.21)
, (3.21)
i=1,2; j=1,2,3….
“Точное” значение 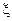 находится в пределах
находится в пределах 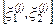 , где
, где
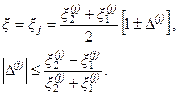 (3.22)
(3.22)
3.3.2. Программная реализация алгоритма по методу аппроксимации на алгоритмическом языке Фортран-90*)
Программа "beta2" предназначена для расчета поперечных волновых чисел h в волноведущем диэлектрическом слое для Н-волн планарного однородного изотропного диэлектрического волновода. Входные и выходные данные такие же, что и в программе "beta1" (см. п. 3.2.3). Вначале программа "beta2" вычисляет верхний и нижний пределы параметра кривизны 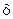 по (3.15) и определяет границы области решения, которые затем использует в качестве начальных значений для итерационной процедуры. В ходе итерационной процедуры происходит обращение к функциям aksi и delta, реализующим вычисления по (3.21).
по (3.15) и определяет границы области решения, которые затем использует в качестве начальных значений для итерационной процедуры. В ходе итерационной процедуры происходит обращение к функциям aksi и delta, реализующим вычисления по (3.21).
!--------------------------------------------------------------
!Программа расчета волнового числа h в волноводном
!диэлектрическом слое для H-волн планарного однородного
!изотропного диэлектрического волновода
Program beta2
!переменный, общие для beta1 и функций aksi и delta
Дата добавления: 2020-10-25; просмотров: 174;










